Water
Content Navigation
CAS Number
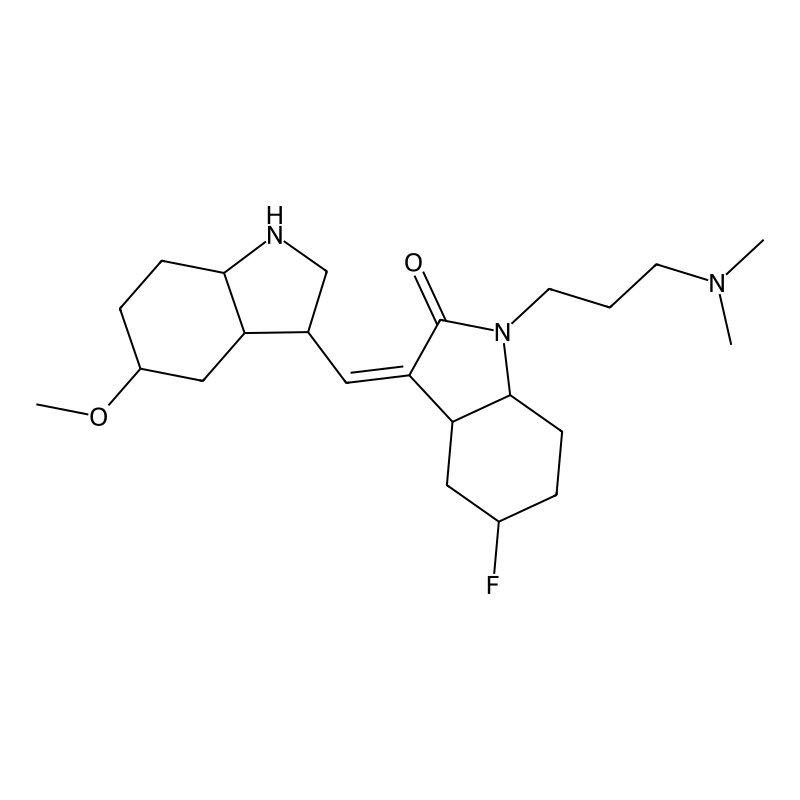
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
solubility
Water dissolves some amount of virtually every solid or gas with wich it comes in contact.
Very soluble in ethanol, methanol, acetone
55.5 mol/L
Synonyms
Canonical SMILES
Understanding Biological Processes
- Solvent of Life: Water's remarkable ability to dissolve a wide range of polar and ionic compounds makes it the universal solvent of life. This allows for essential biological processes like nutrient transportation, cellular reactions, and waste removal .
- Biomolecular Interactions: Water molecules participate in hydrogen bonding, a crucial force influencing the structure and function of biomolecules like proteins and DNA. Research on water's role in these interactions helps us understand vital cellular activities .
Chemical Analysis and Research
- Reaction Medium: Many chemical reactions occur in aqueous solutions (water-based solutions). Water's ability to control reaction rates, maintain temperature, and act as a reactant or product makes it a versatile medium for chemical research .
- Purification and Separation Techniques: Techniques like extraction, precipitation, and chromatography rely on water's different polarities to separate and purify various chemicals. These methods are fundamental tools in analytical chemistry .
Environmental Science and Research
- Hydrological Cycle: Water is the driving force behind the hydrological cycle, which encompasses the movement of water on, above, and below the Earth's surface. Research in this area focuses on understanding water distribution, climate change impacts, and sustainable water management practices .
- Water Quality Monitoring: Water quality is a critical aspect of environmental health. Researchers analyze water samples to assess pollution levels, identify potential contaminants, and monitor the health of ecosystems .
Water, with the chemical formula H₂O, is an inorganic compound essential for life on Earth. It consists of two hydrogen atoms covalently bonded to one oxygen atom, forming a bent molecular structure with an angle of approximately 104.5 degrees between the hydrogen atoms. This unique geometry contributes to its polar nature, where the oxygen atom carries a partial negative charge and the hydrogen atoms carry partial positive charges. Water is transparent, tasteless, odorless, and nearly colorless in small quantities, exhibiting a slight intrinsic blue color due to light absorption at red wavelengths .
Water exists in three states: solid (ice), liquid (water), and gas (water vapor). Its ability to transition between these states under normal terrestrial conditions is a key feature that supports various ecological processes. Water is often referred to as the "universal solvent" due to its capacity to dissolve more substances than any other liquid, making it vital for biological functions and
- Drowning: Inhalation of water can lead to suffocation.
- Electrolyte Imbalance: Drinking excessive amounts of pure water can dilute electrolytes in the body, leading to health problems.
- Contamination: Water contaminated with bacteria, viruses, or toxins can cause various illnesses.
Research on water interactions focuses on its role as a solvent and its behavior in biological systems:
- Hydration Shells: Water molecules surround ions or polar molecules, facilitating solubility through hydration.
- Hydrogen Bonding: The ability of water molecules to form hydrogen bonds affects properties like surface tension and viscosity.
- Biological Membranes: Water interacts with lipid bilayers in cells, influencing membrane fluidity and permeability.
Studies on these interactions are critical for understanding biochemical pathways and ecological dynamics .
Similar Compounds: Comparison with Other Compounds
Several compounds share similarities with water but exhibit distinct properties:
| Compound | Chemical Formula | Key Differences |
|---|---|---|
| Hydrogen Peroxide | H₂O₂ | Contains two oxygen atoms; acts as an oxidizer |
| Ammonia | NH₃ | Composed of nitrogen; less polar than water |
| Methanol | CH₃OH | Alcohol; less effective solvent for ionic compounds |
| Sulfuric Acid | H₂SO₄ | Strong acid; highly corrosive |
While these compounds may share elements with water or have similar structures, their differing properties make them unique in their applications and behaviors .
Molecular Geometry and Bond Structure (Section 2.1)
Covalent Bonding in H₂O (Section 2.1.1)
Water contains two oxygen–hydrogen σ-bonds formed by orbital overlap between the oxygen 2px/2py hybrids and hydrogen 1s orbitals [1] [2]. Each bond length is 0.957 Å in the gas phase [3].
Bond Angle and Molecular Symmetry (Section 2.1.2)
Valence-shell electron-pair repulsion dictates a bent C₂v shape. Lone-pair repulsion contracts the ideal tetrahedral angle (109.5°) to 104.45° in the isolated molecule [4] [5]. The symmetry elements comprise a C₂ principal axis and two σ_v planes [6].
Quantum Mechanical Description (Section 2.1.3)
Early ab-initio work used modified electron-pair functions and Roothaan self-consistent field methods to model the full ten-electron system, successfully reproducing bond angles and dipole moments [7]. Modern polarizable molecular-orbital force fields (e.g., XP3P) incorporate explicit electronic polarization, improving agreement with liquid-state observables [3].
Isotope Variations: H₂O, D₂O and T₂O (Section 2.1.4)
Isotopic substitution raises mass, strengthening hydrogen bonding and shifting thermodynamic parameters. Key data are summarised below.
| Property | H₂O | D₂O | T₂O |
|---|---|---|---|
| Molar mass (g mol⁻¹) | 18.015 [8] | 20.027 [9] | 22.032 [10] |
| Melting point (°C) | 0.00 [11] | 3.82 [9] | 4.49 [10] |
| Boiling point (°C) | 100.00 [11] | 101.4 [9] | ~102.5 (est.) [10] |
| Self-ionisation pK_w at 25 °C | 13.995 [11] | 14.951 [11] | ≈15.0 (calc.) [8] |
| Gas-phase dipole moment (D) | 1.855 [12] | 1.87 [9] | n/a (radioactive) [10] |
Electronic Properties (Section 2.2)
Dipole Moment and Polarity (Section 2.2.1)
In the gas phase, the permanent dipole is 1.855 D [12]. Condensed-phase polarization elevates the effective monomer dipole to 2.6–2.9 D, depending on cluster size and localization scheme [12]. The dipole vector points from the hydrogen bisector toward the oxygen lone-pair region, underpinning the high dielectric constant of 78.5 at 25 °C [13].
Electronic Structure Calculations (Section 2.2.2)
Density-functional and wave-function methods converge on a HOMO–LUMO gap near 12.6 eV, matching photoelectron spectra [14]. Polarizable QM potentials such as PMOw → XP3P accurately reproduce dipole derivatives and vibrational intensities [3]. Molecular-orbital diagrams reveal three bonding (σ) orbitals, two non-bonding (n) lone-pair orbitals, and corresponding antibonding σ* levels [15].
Charge Distribution Analysis (Section 2.2.3)
Population analyses produce partial charges of −0.66 e on oxygen and +0.33 e on each hydrogen when constrained to match the experimental dipole [14]. Voronoi deformation density and natural population schemes yield comparable values within ±0.05 e, highlighting method sensitivity [14].
Chemical Reactivity (Section 2.3)
Acid–Base Behaviour (Section 2.3.1)
Water is amphiprotic. Thermodynamically rigorous treatment assigns pKa(H₂O)=14.00 at 25 °C, derived from the ion product Kw=1.00 × 10⁻¹⁴ [16]. Values of 15.7 arise only when the solvent concentration is erroneously inserted into equilibrium expressions [17].
Self-Ionisation and pH (Section 2.3.2)
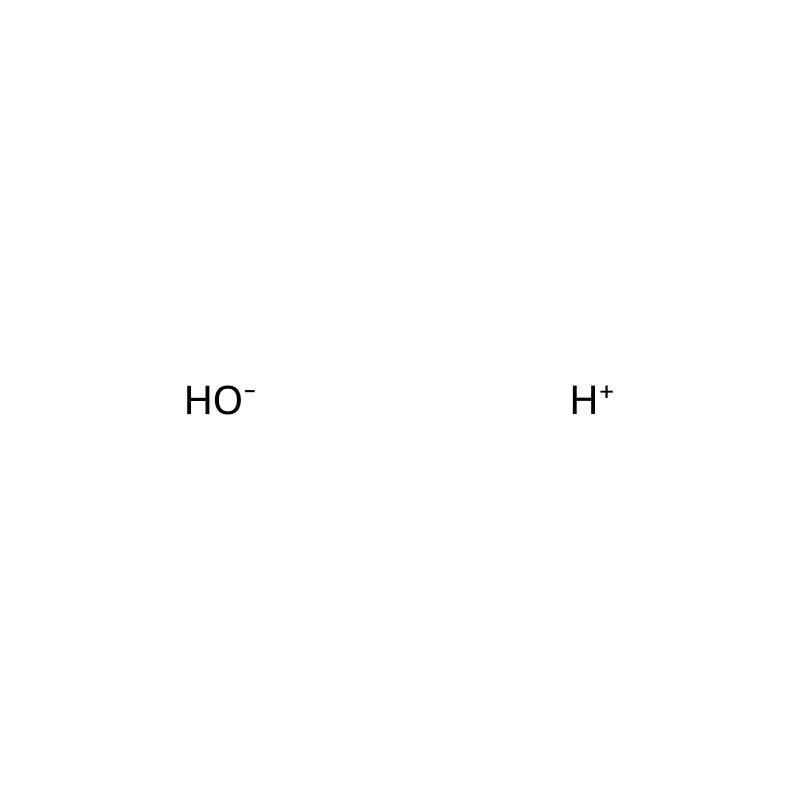
Autoprotolysis: 2 H₂O ⇌ H₃O⁺ + OH⁻. The temperature dependence of K_w is:
| Temperature (°C) | pK_w H₂O | pK_w D₂O |
|---|---|---|
| 0 | 14.95 [11] | 15.97 [11] |
| 25 | 13.995 [11] | 14.951 [11] |
| 60 | 13.43 [11] | 14.30 [11] |
At 25 °C, neutral pH is 7.00 where [H₃O⁺]=[OH⁻]=1.00 × 10⁻⁷ mol L⁻¹ [18].
Redox Properties (Section 2.3.3)
Standard electrode potentials relative to the standard hydrogen electrode:
| Half-Reaction | E⁰ (V) |
|---|---|
| O₂ + 4 H⁺ + 4 e⁻ → 2 H₂O | +1.23 [19] |
| 2 H₂O → O₂ + 4 H⁺ + 4 e⁻ | −1.23 [20] [21] |
| 2 H₂O + 2 e⁻ → H₂ + 2 OH⁻ | −0.83 [22] |
Oxidation–reduction potential (ORP) in natural waters typically ranges from −200 mV in anoxic zones to +800 mV under oxidative disinfection [23] [24] [25].
Coordination Chemistry of Water (Section 2.3.4)
Water donates two electrons via the oxygen lone pair, functioning as a neutral σ-donor ligand [26]. In octahedral aqua complexes such as [Fe(H₂O)₆]³⁺, ligand–field stabilization and proton transfer govern reactivity [26]. Metal–hydroxo species arising from deprotonation are central to catalytic water-splitting cycles, where O–H activation and O–O bond formation dictate efficiency [27].
Data Tables
Selected Geometric and Electronic Benchmarks
| Parameter | Gas-Phase Value | Condensed-Phase Trend |
|---|---|---|
| O–H bond length (Å) | 0.957 [3] | +0.01 Å in ice [8] |
| H–O–H angle (°) | 104.45 [4] | ≈104.5 in liquid [28] |
| HOMO–LUMO gap (eV) | 12.6 [14] | Bandwidth narrows by ≈1 eV in liquid [3] |
| Static dielectric constant | 1.0 (vacuum reference) | 78.5 at 25 °C [13] |
Isotopic Effects on Ionisation Constant
| Isotope | ΔpK_w vs H₂O at 25 °C |
|---|---|
| D₂O | +0.956 [11] |
| T₂O | ≈+1.0 (extrapolated) [8] |
Heat Capacity and Thermal Conductivity
Water exhibits exceptional thermal properties that distinguish it from most other substances. The specific heat capacity of liquid water at 15°C is remarkably high at 4.187 kilojoules per kilogram per Kelvin [1] [2] [3]. This value significantly exceeds that of most common materials, reflecting water's unique molecular structure and hydrogen bonding network. In comparison, ice possesses a specific heat capacity of 2.108 kilojoules per kilogram per Kelvin, while water vapor exhibits 1.996 kilojoules per kilogram per Kelvin [2] [3].
The thermal conductivity of water demonstrates temperature-dependent behavior, increasing systematically with rising temperature in the liquid phase. At 20°C, liquid water exhibits a thermal conductivity of 0.598 watts per meter per Kelvin [2] [4]. Detailed measurements reveal that thermal conductivity rises from 0.5558 watts per meter per Kelvin at 0.01°C to 0.6770 watts per meter per Kelvin at 99.6°C [4]. This positive temperature dependence reflects enhanced molecular motion and energy transfer mechanisms at elevated temperatures.
The molecular basis for water's exceptional heat capacity lies in its hydrogen bonding network [1]. Energy absorption initially disrupts intermolecular hydrogen bonds before increasing the kinetic energy of individual molecules. This two-stage energy absorption process accounts for the substantial thermal energy required to raise water's temperature compared to substances lacking extensive hydrogen bonding.
Enthalpy and Entropy Considerations
Water's enthalpy and entropy properties reveal complex thermodynamic behavior influenced by molecular interactions and phase transitions. The latent heat of fusion for ice melting equals 334 kilojoules per kilogram, while the latent heat of vaporization at 100°C reaches 2,256 kilojoules per kilogram [2] [3]. These substantial energy requirements reflect the strength of hydrogen bonding in both solid and liquid phases.
Computational studies using molecular dynamics simulations provide detailed insights into water's entropy characteristics [5] [6]. Ab initio molecular dynamics calculations demonstrate that liquid water's absolute entropy comprises approximately two-thirds translational contributions, one-third rotational contributions, and five percent conformational effects [5]. The entropy change during melting equals 22.0 joules per Kelvin per mole, calculated from the equilibrium condition where Gibbs free energy equals zero at the melting point [7].
For the vaporization process, entropy increases dramatically by 109.4 joules per Kelvin per mole, reflecting the transition from ordered liquid structure to disordered gaseous state [7]. These entropy changes illustrate water's tendency toward increased molecular disorder during phase transitions, consistent with fundamental thermodynamic principles.
Free Energy in Aqueous Systems
The Gibbs free energy of water systems governs phase equilibria and thermodynamic stability. At phase transition temperatures, free energy changes equal zero, establishing equilibrium conditions between coexisting phases [7] [8]. For ice-water equilibrium at 0°C, the relationship ΔG = ΔH - TΔS = 0 enables calculation of entropy changes from enthalpy measurements.
Advanced computational methods utilizing Monte Carlo simulations and free-energy perturbation theory provide precise free energy calculations for aqueous systems [5] [9] [10]. These studies reveal that free energy calculations achieve uncertainties of approximately 0.05 kilocalories per mole for hydration processes, while enthalpy determinations exhibit uncertainties around 0.4 kilocalories per mole [9] [10].
The temperature dependence of free energy follows van't Hoff relationships, where enthalpy and entropy contributions can be separated through temperature-dependent measurements [10]. Experimental validation shows excellent agreement between computational predictions and experimental data, with free energies within 1.6 kilojoules per mole and entropies within 3.6 joules per Kelvin per mole across various water models [5].
Phase Behavior
Phase Diagram and Critical Points
Water's phase diagram exhibits unique characteristics that reflect its molecular structure and intermolecular interactions. The critical point occurs at 373.946°C and 22.064 megapascals, with a critical density of 0.322 grams per cubic centimeter [2] [3]. Above this temperature and pressure, distinct liquid and vapor phases cease to exist, and water exists as a supercritical fluid with properties intermediate between gas and liquid phases [11] [12] [13].
The phase equilibrium curves demonstrate water's unusual behavior compared to most substances. The solid-liquid equilibrium line exhibits a negative slope in pressure-temperature space, indicating that ice density remains lower than liquid water density [14] [15]. This characteristic enables ice to float on liquid water and contributes to water's ecological significance.
Phase boundaries represent thermodynamic equilibria where chemical potentials of adjacent phases remain equal [16] [17]. The fusion curve describes solid-liquid equilibrium, the vaporization curve represents liquid-vapor equilibrium, and the sublimation curve characterizes solid-vapor transitions [11]. These curves intersect at the triple point, where all three phases coexist simultaneously.
Triple Point Phenomena
The triple point of water occurs at precisely 0.01°C (273.16 Kelvin) and 611.657 pascals [11] [2] [3]. This unique combination of temperature and pressure allows solid ice, liquid water, and water vapor to coexist in thermodynamic equilibrium [11] [18]. The triple point serves as a fundamental reference point in thermodynamics and forms the basis for the Kelvin temperature scale definition [18].
At the triple point, phase transition kinetics become particularly significant. Below the triple point pressure, solid ice undergoes direct sublimation to vapor without passing through the liquid phase [11]. This behavior explains why ice sublimates in vacuum conditions or at very low pressures, such as those encountered in outer space environments.
The triple point represents a singular condition where three-phase equilibrium exists. Any deviation in temperature or pressure from these exact values results in the disappearance of one or more phases, demonstrating the precise nature of thermodynamic equilibrium conditions [17] [12].
Supercritical Water Characteristics
Supercritical water exhibits remarkable properties that differ substantially from both liquid and gaseous phases. Above the critical temperature of 374°C and critical pressure of 22.1 megapascals, water becomes a supercritical fluid with unique solvent characteristics [19] [13] [20] [21]. Unlike ambient liquid water, supercritical water lacks the extensive hydrogen bonding network that characterizes normal liquid behavior [20].
Structural studies using ab initio molecular dynamics simulations reveal that supercritical water can be compressed continuously from gas-like to liquid-like densities without undergoing phase transitions [22] [23]. The effective molecular dipole moment varies systematically with density, correlating linearly with hydrogen bond coordination numbers across the entire density range [22] [23].
The dielectric constant of supercritical water decreases dramatically with increasing temperature, dropping from 80 at room temperature to values equivalent to organic solvents at elevated temperatures [19]. At 200°C, water's dielectric constant equals that of methanol and ethanol, while at 300°C it resembles acetone [19]. This property transformation enables supercritical water to dissolve both polar and nonpolar compounds, making it valuable for industrial applications [21].
Dynamic properties also change significantly in the supercritical region. Hydrogen bond lifetimes decrease substantially and follow Arrhenius-type temperature dependence, while remaining relatively unaffected by density variations along supercritical isotherms [22] [23]. Self-diffusion coefficients vary dramatically with density changes but scale linearly with temperature along isochores [22] [23].
Anomalous Properties
Density Maximum at 4°C
Water exhibits its most famous anomaly through a density maximum at 4°C, where liquid water reaches its highest density of 999.975 kilograms per cubic meter [14] [24] [25] [26]. This behavior contradicts the normal expectation that liquids become progressively denser as temperature decreases. Below 4°C, water actually expands upon further cooling, demonstrating negative thermal expansion behavior [24] [27].
Molecular dynamics simulations using the TIP4P/2005 water model accurately reproduce this density anomaly with remarkable precision [14] [25]. The maximum density shifts to lower temperatures under increased pressure, with approximately 45 bars required to decrease the maximum density temperature by one degree Celsius [25]. This pressure dependence reflects the underlying molecular mechanisms governing water's structural organization.
The physical origin of the density maximum involves competing effects between hydrogen bonding and van der Waals interactions [15] [27]. At higher temperatures, thermal motion disrupts hydrogen bonds, allowing molecules to pack more efficiently through van der Waals forces. As temperature decreases toward 4°C, strengthening hydrogen bonds begin to impose tetrahedral coordination geometry, creating more open molecular arrangements that reduce density [15] [27].
Negative Thermal Expansion Coefficient
Between 0°C and 4°C, water demonstrates negative thermal expansion, where heating actually causes the liquid to contract rather than expand [28] [24] [15] [29]. This anomalous behavior results from the competition between hydrogen bond formation and thermal motion effects [15] [27]. The thermal expansion coefficient becomes negative in this temperature range, reaching zero precisely at the density maximum temperature.
Experimental measurements and theoretical calculations confirm that negative thermal expansion originates from structural rearrangements in water's hydrogen bond network [29] [27]. As temperature increases from 0°C toward 4°C, disruption of ice-like tetrahedral structures allows molecules to adopt more compact configurations, reducing overall volume despite thermal expansion effects [27].
This property has profound ecological consequences. During winter cooling, water at 4°C remains densest and settles to the bottom of lakes and oceans, while cooler water near 0°C becomes less dense and rises to the surface [24] [30]. This stratification enables ice formation on water surfaces while maintaining liquid water beneath, protecting aquatic life during freezing conditions [24] [30].
High Surface Tension and Viscosity
Water exhibits exceptionally high surface tension compared to other common liquids, measuring 72.8 millinewtons per meter at 20°C [31] [32] [33]. This elevated surface tension, approximately three times higher than expected for non-hydrogen-bonded liquids, arises from missing hydrogen bonds at the air-water interface [31]. Recent experimental studies reveal that freshly created water surfaces exhibit even higher surface tension values around 90 millinewtons per meter, with relaxation occurring over millisecond timescales [31].
The temperature dependence of surface tension follows a predictable pattern, decreasing systematically as temperature increases toward the critical point [34] [35] [32] [33]. International standards provide precise formulations for surface tension from 0.01°C to 374°C, with interpolating equations that accurately represent experimental values within stated uncertainties [32] [33].
Water's viscosity demonstrates strong temperature dependence, decreasing exponentially as temperature increases [36] [37] [38] [39]. At 20°C, water viscosity equals 1.002 millipascal-seconds, with temperature dependence following empirical relationships developed from precise experimental measurements [38]. The viscosity behavior reflects hydrogen bond network dynamics, where higher temperatures facilitate molecular motion by disrupting intermolecular interactions [40] [39].
Exceptionally High Specific Heat Capacity
Water's specific heat capacity of 4.187 kilojoules per kilogram per Kelvin represents one of the highest values among common liquids [1] [41]. This exceptional property enables water to absorb substantial thermal energy with minimal temperature change, making it an excellent thermal regulator in both biological and environmental systems [41].
The molecular basis for high specific heat capacity involves energy distribution between translational, rotational, and vibrational molecular motions [1] [41]. Additionally, energy absorption disrupts hydrogen bonds before increasing molecular kinetic energy, creating a two-stage process that requires substantial energy input for temperature increases [41].
Computational studies demonstrate that quantum corrections to heat capacity can reach 60 percent, highlighting the importance of quantum mechanical effects in water's thermal properties [6]. Various water models show different heat capacity predictions, with classical molecular dynamics simulations generally providing reasonable agreement with experimental values when properly parameterized [6].
Colligative Properties
Freezing Point Depression
Freezing point depression occurs when solutes dissolve in water, lowering the temperature at which solidification begins [42] [43] [44]. This colligative property depends on the concentration of dissolved particles rather than their chemical identity [44] [45]. The phenomenon explains why seawater remains liquid below 0°C and why antifreeze solutions prevent engine coolant from freezing [43] [44].
The physical mechanism involves disruption of the equilibrium between liquid and solid phases [42] [43]. Solute particles interfere with the formation of ordered ice crystal structures, requiring lower temperatures to achieve solid-liquid equilibrium [43] [46]. This occurs because solute presence reduces the chemical potential of the liquid phase relative to the pure solid phase [42].
Common examples include road salt application during winter weather, where sodium chloride lowers the freezing point of water on road surfaces [43] [46]. In ice cream production, sugar serves as the solute that depresses the freezing point, allowing the mixture to remain partially liquid even at temperatures well below 0°C [46].
Boiling Point Elevation
Boiling point elevation represents the increase in boiling temperature when non-volatile solutes dissolve in water [47] [48] [49]. This property results from reduced vapor pressure of the solution compared to pure water, requiring higher temperatures to achieve vapor pressure equilibrium with atmospheric pressure [47] [48].
The elevation effect occurs because solute particles occupy positions at the liquid surface, reducing the number of water molecules available for vapor phase transition [50] [49]. According to Raoult's law, vapor pressure reduction correlates directly with solute concentration, leading to proportional boiling point increases [48] [49].
Practical applications include enhanced radiator performance in automotive cooling systems, where dissolved antifreeze raises the boiling point above 100°C, preventing coolant vaporization under high-temperature operating conditions [44] [45]. Cooking applications also demonstrate this effect when salt addition to water increases boiling temperatures [47].
Osmotic Pressure Effects
Osmotic pressure develops when water molecules move through semipermeable membranes to equalize solute concentrations on both sides [44] [51] [52]. This process continues until hydrostatic pressure balances the tendency for water movement, establishing osmotic equilibrium [44] [52].
The magnitude of osmotic pressure depends on solute particle concentration, temperature, and the van't Hoff factor representing particle dissociation [51] [53] [54]. Ionic compounds exhibit higher osmotic pressures than molecular solutes due to dissociation into multiple particles upon dissolution [53] [54].
Biological systems extensively utilize osmotic pressure for water transport and cellular regulation [44] [55]. Industrial applications include reverse osmosis water purification, where applied pressure exceeds osmotic pressure to force water through membranes while excluding dissolved contaminants [55].
Mathematical Models for Colligative Properties
Mathematical relationships quantify colligative property magnitudes based on solution composition and thermodynamic parameters. Freezing point depression follows the equation ΔTf = -i × Kf × m, where i represents the van't Hoff factor, Kf equals the cryoscopic constant (1.86 K·kg/mol for water), and m denotes molality [43] [56] [57] [54].
Boiling point elevation utilizes the analogous relationship ΔTb = i × Kb × m, with Kb representing the ebullioscopic constant (0.51 K·kg/mol for water) [48] [56] [57]. Osmotic pressure calculations employ π = i × M × R × T, where M represents molarity, R equals the ideal gas constant, and T denotes absolute temperature [44] [51] [57].
The van't Hoff factor (i) accounts for particle dissociation or association effects in solution [56] [53] [54]. For non-electrolytes, i approaches unity, while ionic compounds exhibit i values corresponding to the number of ions produced per formula unit [53] [54]. Deviations from ideal behavior occur due to ion pairing and other intermolecular interactions [54].
Physical Description
Liquid
Clear colorless odorless liquid; [NTP]
Color/Form
Liquid
XLogP3
Hydrogen Bond Acceptor Count
Hydrogen Bond Donor Count
Exact Mass
Monoisotopic Mass
Boiling Point
99.974 °C
Heavy Atom Count
Taste
Density
0.9950 g/cu cm at 25 °C
Chemical and physical properties[Table#8152]
Expands on freezing. Temp of max density 3.98 °C. density: 1.000000g/mL at 3.98 °C; 0.917 g/cc at 0 °C (ice); 0.999868 at 0 °C/4 °C (liquid)
Weight of sea water: approximately 63.93 lb/cu ft at 15 °C; density of sea water: approximately 1.025 g/cu cm at 25 °C
Ice Properties[Table#8154]
LogP
Odor
Melting Point
0 °C
UNII
Related CAS
191612-63-2
25766-61-4
163734-19-8
151733-06-1
155964-99-1
146915-49-3
70232-06-3
181895-39-6
139322-39-7
144442-59-1
151517-94-1
151733-07-2
139322-38-6
163734-21-2
148076-13-5
158061-35-9
148076-12-4
163734-20-1
79800-59-2
142473-62-9
31014-12-7
142473-64-1
191612-61-0
151517-96-3
25655-83-8
144442-58-0
146915-50-6
142473-63-0
GHS Hazard Statements
Reported as not meeting GHS hazard criteria by 1814 of 1820 companies (only ~ 0.3% companies provided GHS information). For more detailed information, please visit ECHA C&L website
Drug Indication
FDA Label
NCI Cancer Drugs
Drugs in the ICE combination: I = Ifosfamide ; C = Carboplatin ; E = Etoposide Phosphate
ICE is used to treat: Hodgkin lymphoma.
Non-Hodgkin lymphoma (NHL).
This combination may also be used with other drugs or treatments or to treat other types of cancer.
Pharmacology
Vapor Pressure
VP: 760 mm Hg at 100 °C
VP: 611.657 Pa at 273.16 K
Other CAS
17778-80-2
Absorption Distribution and Excretion
Wikipedia
Use Classification
Safer Chemical Classes -> Green circle - The chemical has been verified to be of low concern
Fragrance Ingredients
Cosmetics -> Solvent
Methods of Manufacturing
General Manufacturing Information
Wood Product Manufacturing
All Other Basic Inorganic Chemical Manufacturing
Petroleum Lubricating Oil and Grease Manufacturing
Water: ACTIVE
Some bottled waters contain fluoride, and some do not. Fluoride can occur naturally in source waters used for bottling or be added. Most bottled waters contain fluoride at levels that are less than optimal for good oral health.
People with compromised immune systems may want to take special precautions with the water they drink. In healthy individuals, the parasite Cryptosporidium can cause illness; however, for those with weakened immune systems, it can cause severe illness and possibly death. Look for bottled water treatments that protect against Cryptosporidium, which include: Reverse Osmosis Distillation Filtration with an absolute 1 micron filter.
The proper amount of fluoride from infancy through old age helps prevent and control tooth decay. Community water fluoridation is a widely accepted practice for preventing and controlling tooth decay by adjusting the concentration of fluoride in the public water supply
According to the EPA, approximately 286 million Americans receive their tap water from a community water system. These public water systems are monitored and regulated as set by the EPA. An estimated 15% of Americans, or about 45 million people, get their water from private ground water wells that are not subject to EPA regulations. Private ground water wells can provide safe, clean water. However, well water can also become contaminated, leading to illness. It is the responsibility of well owners to maintain and treat their well.
For more General Manufacturing Information (Complete) data for Water (10 total), please visit the HSDB record page.