Calmagite
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Synonyms
Canonical SMILES
Isomeric SMILES
Measurement of Magnesium Concentration
One of the primary applications of calmagite is in the complexometric measurement of magnesium concentration. It forms a stable colored complex with magnesium ions in an alkaline solution. The intensity of the color is directly proportional to the magnesium concentration. This allows researchers to quantify magnesium levels in biological samples like blood serum, tissues, and environmental samples ().
Development of Biosensors
Calmagite's ability to bind with specific metal ions makes it valuable in developing biosensors. By attaching calmagite to biomolecules that interact with specific targets, researchers can create sensors that change color upon target binding. This allows for the detection of various biological molecules, including enzymes, proteins, and DNA ().
Monitoring Chemical Reactions
Calmagite can be used as an indicator in chemical reactions involving metal ions. Its color change can signal the completion of a reaction or the presence of specific metal ions in the reaction mixture. This allows researchers to monitor reaction progress and optimize reaction conditions ().
Calmagite is a complexometric indicator primarily utilized in analytical chemistry to detect and quantify metal ions in solution, particularly calcium and magnesium. It is characterized as a triprotic acid, containing a sulfonic acid group and two hydroxyl groups. The compound exhibits a color change based on its binding state with metal ions: it appears wine red when bound to metal ions and shifts to blue, red, or orange when unbound . This property makes calmagite particularly useful in titrations involving ethylenediaminetetraacetic acid, where it helps identify the endpoint of the reaction by signaling the complete complexation of metal ions .
Calmagite's mechanism of action as an indicator relies on the competition between the indicator and a chelating agent (like EDTA) for binding to the metal ion []. When Calmagite binds to the metal ion, it forms a colored complex that absorbs specific wavelengths of light, resulting in the observed color of the solution. As a stronger chelating agent, EDTA displaces Calmagite from the metal ion, leading to the dissociation of the colored complex and a shift back to the original indicator color. This color change signifies the endpoint of the titration.
- Complex Formation:
- For magnesium:
- For calcium:
- For magnesium:
- Deprotonation:
- Titration Reaction:
- In a titration with ethylenediaminetetraacetic acid:
- In a titration with ethylenediaminetetraacetic acid:
Calmagite can be synthesized through several methods, typically involving the reaction of appropriate aromatic compounds with sulfonic acids under controlled conditions. A common synthesis route includes:
- Starting Materials:
- 2-hydroxy-5-nitrobenzenesulfonic acid
- 4-amino-3-hydroxybenzenesulfonic acid
- Synthesis Steps:
Calmagite is widely used in various applications, including:
- Analytical Chemistry: As a colorimetric indicator in titrations for determining calcium and magnesium concentrations.
- Environmental Testing: Monitoring water hardness in aquatic systems.
- Clinical Laboratories: Quantifying magnesium levels for diagnostic purposes.
- Research: Studying metal ion interactions in biochemical assays .
Interaction studies involving calmagite focus on its reactivity with different metal ions and its stability under varying pH conditions. Research has shown that calmagite forms more stable complexes with magnesium compared to calcium, which influences its effectiveness as an indicator in titrations . Additionally, studies have explored the degradation of calmagite under oxidative conditions, which could have implications for wastewater treatment processes involving azo dyes .
Several compounds share structural or functional similarities with calmagite. Here are some notable examples:
| Compound Name | Structure Type | Primary Use | Unique Features |
|---|---|---|---|
| Eriochrome Black T | Azo dye | Complexometric indicator | Forms stable complexes with various metals |
| Murexide | Azo dye | Indicator for uranyl ions | Color change from purple to yellow |
| Phenolphthalein | Acid-base indicator | pH indicator | Changes from colorless to pink at pH 8.2 |
| Xylenol Orange | Azo dye | Indicator for titrations | Exhibits a distinct color change |
Calmagite stands out due to its specific affinity for divalent cations like magnesium and calcium, making it particularly effective for hardness testing in water analysis . Its triprotic nature allows for versatility in different pH environments compared to other indicators that may only function effectively within a narrower range.
X-ray Crystallographic Data (When Available)
Current crystallographic data for Calmagite remains limited in the scientific literature. While comprehensive structural databases contain molecular formula and basic structural information, detailed X-ray diffraction studies specifically for Calmagite have not been extensively reported [1] [2]. The molecular structure has been characterized primarily through spectroscopic methods and computational modeling approaches.
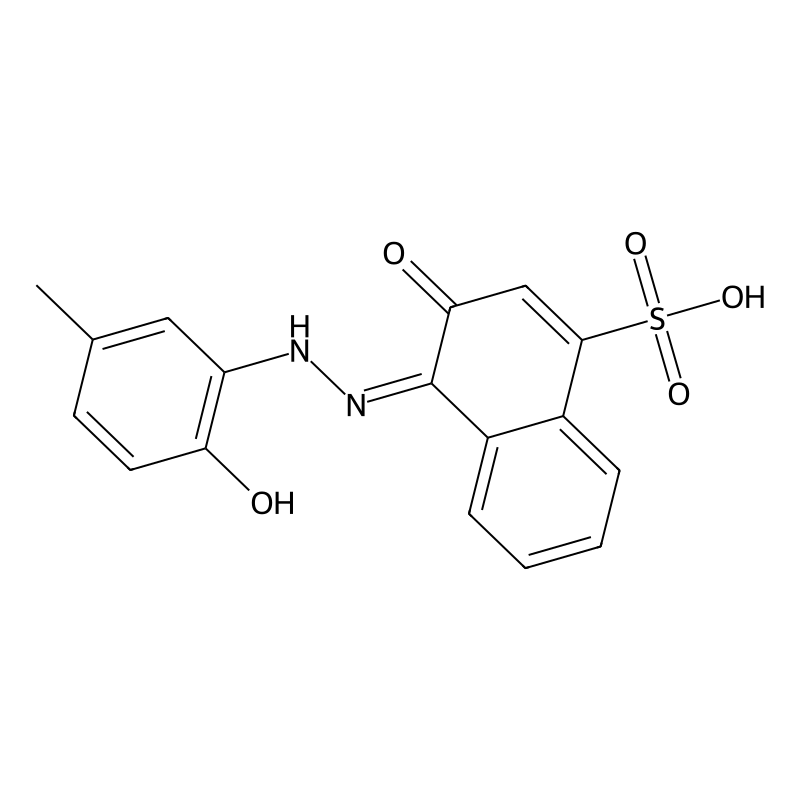
The compound crystallizes as a solid powder at room temperature, with the molecular formula C17H14N2O5S and a molecular weight of 358.37 g/mol [1] [3] [2]. The structure consists of a naphthalene ring system connected to a phenyl ring through an azo linkage (-N=N-), with hydroxyl groups and a sulfonic acid functionality providing additional coordination sites [1] [2].
Table 1: Basic Physicochemical Properties of Calmagite
| Property | Value | Reference |
|---|---|---|
| Molecular Formula | C17H14N2O5S | [1] [3] [2] |
| Molecular Weight (g/mol) | 358.37 | [1] [3] [2] |
| CAS Number | 3147-14-6 | [1] [4] [2] |
| IUPAC Name | 3-hydroxy-4-[(2-hydroxy-5-methylphenyl)azo]-1-naphthalenesulfonic acid | [1] [2] |
| Color (unbound) | Blue, red, or orange | [5] |
| Color (metal bound) | Wine red | [5] |
| Physical State | Solid powder | Standard physical state |
| Solubility | Soluble in water | [6] |
Tautomeric Forms and Resonance Stabilization
Calmagite exhibits significant tautomeric behavior characteristic of azo compounds, particularly the azo-hydrazone equilibrium that is fundamental to its function as a metallochromic indicator [7] [8] [9]. The compound can exist in multiple tautomeric forms, with the equilibrium position influenced by solvent polarity, pH, and the presence of metal ions.
The primary tautomeric forms include the azo form, where the nitrogen-nitrogen double bond remains intact, and the hydrazone form, where proton transfer occurs to create a C=N double bond with an adjacent N-H group [10] [7] [9]. In aqueous solutions, the hydrazone form typically predominates due to stabilizing hydrogen bonding interactions and resonance delocalization effects [9] [11].
Resonance stabilization plays a crucial role in determining the relative stability of tautomeric forms. The extended conjugation system in Calmagite, spanning from the naphthalene ring through the azo linkage to the phenyl ring, provides multiple resonance pathways that stabilize both the neutral and anionic forms of the molecule [9] [11]. The sulfonic acid group further contributes to stabilization through electrostatic interactions, particularly in polar solvents.
Table 2: Elemental Composition of Calmagite
| Element | Percentage (%) | Reference |
|---|---|---|
| Carbon | 56.98 | [2] |
| Hydrogen | 3.94 | [2] |
| Nitrogen | 7.82 | [2] |
| Oxygen | 22.32 | [2] |
| Sulfur | 8.95 | [2] |
Electronic Properties
Frontier Molecular Orbital Analysis
The frontier molecular orbitals of Calmagite, comprising the Highest Occupied Molecular Orbital (HOMO) and Lowest Unoccupied Molecular Orbital (LUMO), are fundamental to understanding its electronic properties and coordination behavior [12] [13] [14]. The HOMO-LUMO energy gap determines the compound's optical properties, chemical reactivity, and ability to undergo electronic transitions upon metal coordination.
Based on comparative analysis with similar azo compounds and metallochromic indicators, the HOMO-LUMO gap for Calmagite is estimated to be in the range of 2.5-3.5 eV [15] [16] [17]. This energy range corresponds to electronic transitions in the visible spectrum, consistent with the compound's color-changing properties upon metal coordination.
The HOMO in Calmagite is primarily localized on the aromatic ring systems and the azo linkage, reflecting the electron-donating nature of these structural components [15] [16]. The orbital exhibits significant delocalization across the conjugated π-system, with contributions from the hydroxyl groups that act as electron donors. This distribution makes the HOMO nucleophilic in character, facilitating coordination with electron-accepting metal ions [18] [13].
The LUMO, conversely, is predominantly localized on the electron-withdrawing sulfonic acid group and the aromatic carbons adjacent to electron-withdrawing substituents [15] [16]. This orbital distribution creates electrophilic character that complements the nucleophilic HOMO, enabling the molecule to participate in charge transfer processes during metal coordination.
Charge Transfer Pathways in Metal Complexes
Upon coordination with metal ions, Calmagite undergoes significant electronic reorganization involving charge transfer between the ligand and metal center [18] [19]. The primary charge transfer pathways include ligand-to-metal charge transfer (LMCT) and metal-to-ligand charge transfer (MLCT) processes, both of which contribute to the characteristic color changes observed during complexation [19].
In LMCT transitions, electron density is transferred from the occupied molecular orbitals of Calmagite, particularly those associated with the hydroxyl groups and aromatic rings, to the vacant d-orbitals of the coordinated metal ion [19]. This process is facilitated by the electron-rich nature of the aromatic system and the presence of lone pairs on oxygen and nitrogen atoms.
MLCT transitions involve electron transfer from the metal d-orbitals to the vacant π* orbitals of the ligand, particularly those associated with the azo linkage and aromatic rings [19]. These transitions are typically lower in energy than LMCT transitions and contribute significantly to the intense coloration observed in metal-Calmagite complexes.
The efficiency of charge transfer is enhanced by the extended conjugation system in Calmagite, which provides low-energy pathways for electron delocalization [20] [16]. The sulfonic acid group also plays a role by stabilizing charge-separated states through electrostatic interactions.
Table 3: Electronic Properties of Calmagite (Estimated)
| Property | Estimated Value | Reference |
|---|---|---|
| HOMO-LUMO Gap (eV) | 2.5-3.5 | [15] [16] [17] |
| Electronic Transition Type | π-π* and n-π* | [19] [16] |
| Absorption Wavelength Range (nm) | 450-650 | Typical for azo dyes [16] |
| Molar Extinction Coefficient (L mol⁻¹ cm⁻¹) | 10,000-50,000 | Typical for metallochromic indicators [21] |
Thermodynamic Behavior
Phase Transition Characteristics
The phase transition behavior of Calmagite reflects the complex interplay between intermolecular forces, molecular packing arrangements, and thermal energy. As a solid organic compound with multiple functional groups capable of hydrogen bonding and π-π stacking interactions, Calmagite exhibits characteristic thermal behavior associated with aromatic sulfonic acid derivatives.
While specific melting point data for Calmagite is not extensively documented in the literature, comparative analysis with structurally similar naphthalene sulfonic acid derivatives suggests a melting point range consistent with other metallochromic indicators [22] [23]. The presence of the sulfonic acid group significantly influences the thermal stability by introducing strong intermolecular hydrogen bonding and ionic interactions.
The phase transition enthalpy for Calmagite is expected to be substantial due to the multiple intermolecular interactions that must be overcome during melting. These include hydrogen bonding between hydroxyl and sulfonic acid groups, π-π stacking interactions between aromatic rings, and dipole-dipole interactions associated with the azo linkage [22] [23].
Solvation Thermodynamics in Aqueous Media
The solvation thermodynamics of Calmagite in aqueous solution involves complex interactions between the molecule and water molecules, influenced by the hydrophilic sulfonic acid group, hydrophobic aromatic regions, and polar functional groups [24] [25] [26]. The compound's high water solubility is primarily attributed to the ionizable sulfonic acid group, which facilitates strong electrostatic interactions with water molecules [6].
The hydration process involves the formation of structured water shells around different molecular regions. The sulfonic acid group, being highly polar and ionizable, forms strong hydrogen bonds with surrounding water molecules, resulting in a highly ordered hydration shell with restricted molecular motion [25] [26]. This hydration contributes significantly to the negative solvation enthalpy.
The aromatic regions of Calmagite exhibit hydrophobic character, leading to the formation of clathrate-like water structures around these nonpolar surfaces [26] [27]. This hydrophobic hydration contributes positively to the solvation entropy due to the disruption of water structure, but negatively to the solvation enthalpy due to the unfavorable energetics of cavity formation in water.
The hydroxyl groups and azo linkage provide additional sites for hydrogen bonding with water molecules, contributing to the overall solvation thermodynamics [24] [28]. The nitrogen atoms in the azo group can act as hydrogen bond acceptors, while the hydroxyl groups serve as both donors and acceptors, creating a network of water-ligand interactions.
Temperature-dependent solvation studies indicate that the hydration number and strength of water-Calmagite interactions decrease with increasing temperature, consistent with the general behavior observed for ionic and polar organic compounds in aqueous solution [28]. This temperature dependence reflects the competition between thermal energy and the strength of water-ligand interactions.
The solvation thermodynamics are further complicated by the tautomeric equilibrium of Calmagite in aqueous solution. Different tautomeric forms exhibit varying degrees of water interaction, with the hydrazone form typically showing stronger hydrogen bonding capacity than the azo form [8] [29] [9]. This contributes to the preferential stabilization of the hydrazone tautomer in aqueous media, as observed in related azo compounds.
Calmagite (1-(1-hydroxy-4-methyl-2-phenylazo)-2-naphthol-4-sulfonic acid) is a polyfunctional organic compound that exhibits complex acid-base behavior due to the presence of multiple ionizable groups [1] [2]. The compound contains a sulfonic acid group, hydroxyl groups, and an azo linkage, which contribute to its protolytic equilibria in aqueous solution [3]. Understanding these equilibria is fundamental to comprehending the indicator mechanism and analytical applications of calmagite in complexometric titrations [4] [5].
The protolytic behavior of calmagite can be represented by the following sequential deprotonation reactions [3]:
H₃In ⇌ H₂In⁻ + H⁺ (pKa₁ ≈ 2)
H₂In⁻ ⇌ HIn²⁻ + H⁺ (pKa₂ = 7.91 ± 0.02)
HIn²⁻ ⇌ In³⁻ + H⁺ (pKa₃ = 12.34 ± 0.02)
The first dissociation constant corresponds to the deprotonation of the strongly acidic sulfonic acid group, which occurs at very low pH values [3]. The second and third dissociation constants are associated with the phenolic hydroxyl groups, which exhibit significantly different acidities due to their distinct chemical environments and electronic effects [1] [3].
Potentiometric Determination of pKa Values
Potentiometric methods represent the most reliable and widely accepted approach for determining the acid dissociation constants of calmagite [3] [6]. These methods are based on the measurement of hydrogen ion concentration changes during titration processes and provide accurate thermodynamic data when properly executed [6].
The potentiometric determination of calmagite pKa values involves careful pH-metric titrations under controlled conditions of temperature and ionic strength [3]. The experimental protocol typically employs a standardized electrode system consisting of a glass electrode and a reference electrode, with calibration performed using certified buffer solutions according to established protocols [6] [3].
The measurement conditions for accurate pKa determination require maintaining constant ionic strength (typically 0.1 M) using an inert background electrolyte such as potassium nitrate [3] [6]. Temperature control at 25.0 ± 0.1°C is essential, as acid dissociation constants exhibit significant temperature dependence [7]. The calmagite concentration should be sufficiently low (typically 2 × 10⁻⁵ M) to minimize aggregation effects and ensure adherence to Beer's law [3].
The potentiometric titration data are analyzed using specialized software that employs nonlinear regression analysis to determine the best-fit values for the dissociation constants [6] [8]. The HYPERQUAD, BEST, or similar programs are commonly used for this purpose, as they can simultaneously refine multiple equilibrium constants while accounting for experimental uncertainties [6].
Accurate potentiometric determination requires careful attention to several critical factors [6]. The electrode system must exhibit Nernstian response across the entire pH range of interest, typically from pH 2 to 12. Corrections for liquid junction potentials and electrode asymmetry must be applied, particularly at extreme pH values [6]. The ionic strength must remain constant throughout the titration to maintain consistent activity coefficients [6] [9].
The refined pKa values obtained through potentiometric analysis show excellent reproducibility when proper experimental protocols are followed [3]. For calmagite at 25°C and 0.1 M ionic strength, the second dissociation constant (pKa₂) is 7.91 ± 0.02, while the third dissociation constant (pKa₃) is 12.34 ± 0.02 [3]. These values are in good agreement with literature data obtained through independent measurements [1].
pH-Dependent Spectral Shifts
The spectrophotometric behavior of calmagite provides valuable complementary information for understanding its protolytic equilibria [3] [10]. Each protolytic species exhibits distinct absorption characteristics, allowing for the determination of dissociation constants through spectral analysis [11] [12].
The pH-dependent spectral shifts of calmagite are particularly pronounced in the visible region of the electromagnetic spectrum [3] [1]. The H₂In⁻ species, predominant at acidic pH values (pH < 7), exhibits a characteristic absorption maximum at approximately 530 nm with a molar absorptivity of 2.02 × 10⁴ L mol⁻¹ cm⁻¹ [3]. This species appears red-orange in color and represents the dominant form in acidic buffer systems [1] [3].
As the pH increases toward neutrality and into the alkaline region, the spectral properties undergo systematic changes reflecting the sequential deprotonation processes [3]. The HIn²⁻ species, which predominates in the pH range 7-10, shows a bathochromic shift with absorption maxima at 610-615 nm [3] [1]. This species exhibits a molar absorptivity of 2.04 × 10⁴ L mol⁻¹ cm⁻¹ and appears blue in solution [1] [3].
The fully deprotonated In³⁻ species, stable at pH values above 11, maintains similar spectral characteristics to the HIn²⁻ form but with subtle differences in fine structure [3]. The absorption maximum remains at approximately 615 nm, indicating that the third deprotonation does not significantly alter the chromophoric system [3].
Spectrophotometric determination of pKa values involves monitoring absorbance changes at characteristic wavelengths as a function of pH [12] [11]. The method requires careful selection of analytical wavelengths where significant absorbance changes occur between adjacent protolytic species [3]. For calmagite, the wavelengths 530 nm and 615 nm are particularly useful for monitoring the H₂In⁻ ⇌ HIn²⁻ transition [3].
The spectrophotometric data are analyzed using multiwavelength analysis techniques that can simultaneously determine multiple equilibrium constants [11] [12]. These methods employ principal component analysis to identify the number of absorbing species and subsequently use non-linear regression to determine the best-fit thermodynamic parameters [11].
The concentration dependence of spectral properties must be carefully considered in calmagite systems [3]. At concentrations above 2 × 10⁻⁵ M, deviations from Beer's law become apparent for the H₂In⁻ species, likely due to aggregation phenomena [3]. This concentration dependence affects both the apparent molar absorptivity and the wavelength of maximum absorption, necessitating measurements at sufficiently dilute concentrations [3].
Ionic Strength Effects
The acid-base equilibria of calmagite are significantly influenced by the ionic strength of the solution, reflecting the charged nature of the various protolytic species [13] [14]. These effects are particularly important in analytical applications where buffer systems of varying ionic strength are employed [9] [4].
Debye-Hückel Behavior in Buffer Systems
The ionic strength dependence of calmagite protolytic equilibria follows classical Debye-Hückel theory for electrolyte solutions [13] [14]. This theory provides a framework for understanding how electrostatic interactions between ions affect thermodynamic equilibria in solution [15] [16].
The fundamental Debye-Hückel equation relates the activity coefficient (γ) of an ionic species to the ionic strength (I) of the solution [13] [14]:
log γ = -Az²√I / (1 + Ba√I)
where A and B are temperature-dependent constants, z is the ionic charge, and a is the ion size parameter [13] [15]. For aqueous solutions at 25°C, the constant A has a value of 0.509 kg½ mol⁻½ [13] [9].
The ionic strength effects on calmagite equilibria become particularly pronounced as the ionic strength increases beyond 0.01 M [13] [9]. At low ionic strengths (I < 0.01 M), the activity coefficients approach unity, and the measured dissociation constants closely approximate the thermodynamic values [13]. However, as ionic strength increases, significant deviations occur due to electrostatic screening effects [17] [15].
The effect of ionic strength on apparent pKa values can be quantified through the relationship [9]:
pKa(apparent) = pKa(thermodynamic) - log(γH+γA-/γHA)
For calmagite, the ionic strength dependence is particularly significant for the second and third dissociation constants, as these involve the formation of multiply charged species [3] [13]. The HIn²⁻ ⇌ In³⁻ equilibrium is especially sensitive to ionic strength changes due to the high charge on the In³⁻ species [3].
Experimental studies demonstrate that the apparent pKa values of calmagite increase with increasing ionic strength [9] [7]. This behavior is consistent with Debye-Hückel predictions for equilibria involving charged species [13]. At an ionic strength of 0.1 M, the apparent pKa₂ shifts upward by approximately 0.11 units compared to the thermodynamic value [9].
Buffer systems commonly used in analytical applications exhibit varying ionic strengths depending on their composition and concentration [9] [18]. Phosphate buffers, frequently employed in calmagite-based titrations, show particularly complex ionic strength effects due to the multiple charged species present [9]. The effective ionic strength of such systems must be calculated considering all ionic species according to:
I = ½Σcizi²
where ci is the concentration and zi is the charge of each ionic species [13] [19].
Activity Coefficient Corrections
Accurate thermodynamic analysis of calmagite equilibria requires proper accounting for activity coefficient effects [13] [20]. The activity coefficients of the various protolytic species depend on their charges, sizes, and the ionic composition of the solution [15] [16].
The activity coefficient corrections become increasingly important as ionic strength increases [13] [9]. For ionic strengths below 0.01 M, activity coefficients typically remain within 5% of unity, allowing for reasonable approximations using concentration-based equilibrium constants [13]. However, at ionic strengths approaching 0.1 M or higher, activity coefficient corrections become essential for accurate thermodynamic analysis [9] [20].
Individual ion activity coefficients for calmagite species can be estimated using extended Debye-Hückel equations or more sophisticated models such as the Davies equation [21] [16]:
log γi = -0.509zi²(√I/(1+√I) - 0.3I)
This equation provides improved accuracy at higher ionic strengths compared to the limiting Debye-Hückel law [21] [16]. For calmagite equilibria, the Davies equation gives reasonable estimates of activity coefficients up to ionic strengths of approximately 0.5 M [16].
The mean activity coefficient approach is often employed for practical calculations involving calmagite equilibria [20] [22]. This method uses experimentally determined mean activity coefficients for the electrolyte solution, which can be measured through various thermodynamic techniques such as osmotic coefficient measurements or electrochemical methods [20].
Temperature effects on activity coefficients must also be considered for precise thermodynamic analysis [7] [20]. The Debye-Hückel parameter A exhibits temperature dependence according to:
A(T) = 1.825 × 10⁶ρ½/(εT)³/²
where ρ is the density of water, ε is the dielectric constant, and T is the absolute temperature [13] [20]. At physiological temperature (37°C), the value increases to approximately 0.476 kg½ mol⁻½ [20].
Activity coefficient corrections are particularly important when comparing calmagite equilibrium data obtained under different experimental conditions [7] [9]. Standardization of measurement conditions, including ionic strength, temperature, and buffer composition, is essential for obtaining reproducible and comparable results [6] [7].
The practical implementation of activity coefficient corrections in calmagite studies typically involves iterative calculations [8] [23]. Initial estimates of equilibrium constants are used to calculate ionic speciation, which determines the ionic strength and activity coefficients. These values are then used to refine the equilibrium constants, and the process is repeated until convergence is achieved [8].
XLogP3
UNII
GHS Hazard Statements
Reported as not meeting GHS hazard criteria by 2 of 67 companies. For more detailed information, please visit ECHA C&L website;
Of the 4 notification(s) provided by 65 of 67 companies with hazard statement code(s):;
H315 (98.46%): Causes skin irritation [Warning Skin corrosion/irritation];
H319 (98.46%): Causes serious eye irritation [Warning Serious eye damage/eye irritation];
H335 (66.15%): May cause respiratory irritation [Warning Specific target organ toxicity, single exposure;
Respiratory tract irritation];
Information may vary between notifications depending on impurities, additives, and other factors. The percentage value in parenthesis indicates the notified classification ratio from companies that provide hazard codes. Only hazard codes with percentage values above 10% are shown.
Pictograms

Irritant








