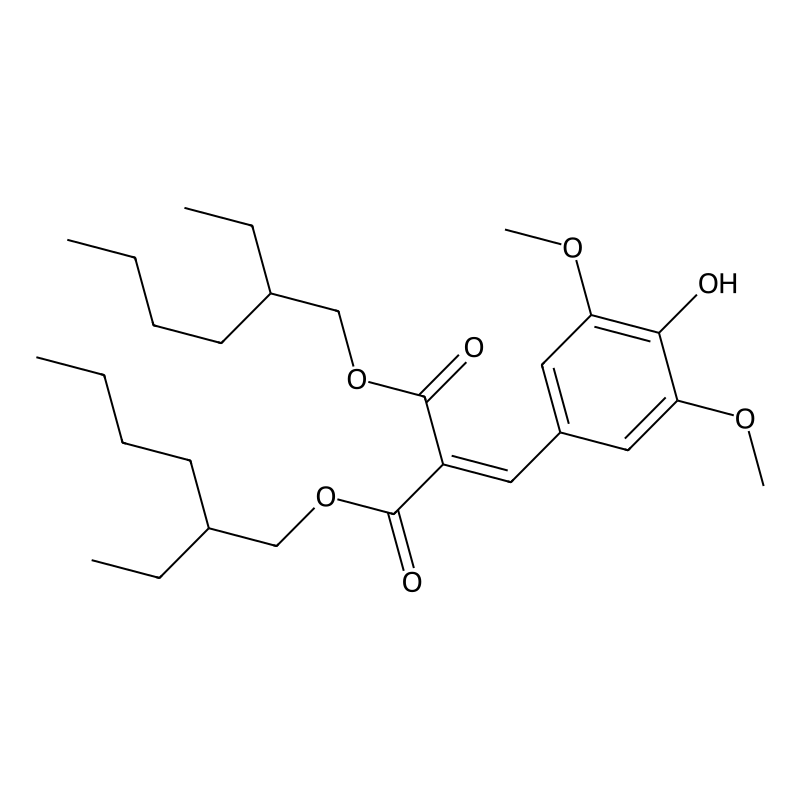
(S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate
![(S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyl...](/img/structure-2d/800/S1489637.png)
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Canonical SMILES
Isomeric SMILES
(S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate, with the chemical formula C36H46O5 and a molecular weight of approximately 558.75 g/mol, is a compound that has garnered attention in biochemical research, particularly in proteomics. This compound features a complex structure that includes a biphenyl moiety, which contributes to its unique properties and potential applications in various scientific fields .
The synthesis of (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate typically involves multi-step organic synthesis techniques. Key steps may include:
- Formation of the biphenyl structure: This can be achieved through coupling reactions involving aryl halides.
- Esterification: The carboxylic acid component is reacted with an alcohol (in this case, the octyloxy group) under acidic conditions to form the ester.
- Chiral resolution: If necessary, chiral reagents or catalysts may be employed to ensure that the final product retains the desired stereochemistry.
Specific methods may vary based on available reagents and desired yield .
The primary applications of (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate lie in:
- Proteomics Research: It serves as a valuable biochemical tool for studying protein interactions and functions.
- Material Science: Due to its unique structural properties, it may find applications in developing advanced materials or coatings.
- Pharmaceutical Development: Its potential biological activity could lead to applications in drug discovery and development .
While specific interaction studies for (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate are scarce, compounds with similar structures often participate in significant interactions with proteins and other biomolecules. These interactions can be explored using techniques such as surface plasmon resonance or nuclear magnetic resonance spectroscopy to assess binding affinities and kinetics.
Several compounds share structural features with (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate. These include:
| Compound Name | Structure | Unique Features |
|---|---|---|
| 4-Octyloxybenzoic acid | C16H26O3 | Simpler structure; used in liquid crystal applications |
| 1-Methylheptyl benzoate | C16H30O2 | Similar ester functionality; potential fragrance applications |
| Biphenyl-4-carboxylic acid | C13H10O2 | Basic biphenyl structure; utilized in polymer chemistry |
The uniqueness of (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate lies in its specific stereochemistry and functional groups that enhance its solubility and reactivity compared to these similar compounds .
(S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate represents a critical model system for studying polar smectic phases in chiral liquid crystals. Its ability to exhibit paraelectric (SmA), ferroelectric (SmC), ferrielectric (SmC$${1/3}^*$$), and antiferroelectric (SmC$$A^*$$) states under varying thermal and electric conditions provides a unique platform for investigating molecular self-assembly and collective polarization dynamics. The compound’s layered structure enables precise modulation of electro-optical responses, making it indispensable for developing next-generation display technologies and photonic devices.
Historical Context and Evolution of Research
Initial investigations in the 1990s focused on characterizing its antiferroelectric properties, with seminal work by Link et al. (1996) demonstrating odd-even layer-dependent ferroelectric coupling in freely suspended films. The discovery of its four distinct subphases (SmC$$\alpha^*$$, SmC$$\gamma^$$, SmC$$^$$, SmC$$_A^*$$) between 1994–2004 revolutionized understanding of chiral smectic polymorphism. Subsequent studies in the 2010s explored doping effects, revealing enhanced dielectric properties when combined with gold nanoparticles. Most recently, convolutional neural networks have achieved 93% accuracy in automated phase classification using texture analysis, marking a paradigm shift in liquid crystal characterization.
Scope and Objectives of the Review
This review systematically evaluates:
- Synthetic pathways and structural determinants of mesophase behavior
- Temperature- and field-dependent phase transitions
- Dielectric relaxation mechanisms and polarization dynamics
- Emerging applications in optoelectronics and nanotechnology
Excluded from scope are pharmacological properties and industrial synthesis protocols, with focus maintained on fundamental materials science.
Theoretical Models Underpinning Chiral Liquid Crystal Compounds
The theoretical understanding of chiral liquid crystal compounds like (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate relies on several fundamental models that describe the complex interplay between molecular structure and mesophase behavior [4] [17]. These theoretical frameworks provide the foundation for predicting and understanding the unique properties exhibited by chiral mesogenic systems.
The Onsager hard-rod model represents one of the most fundamental theoretical approaches for understanding liquid crystalline behavior [17] [22]. This model predicts lyotropic phase transitions based on excluded volume effects, where rod-shaped molecules like biphenylcarboxylate derivatives undergo phase transitions as a function of concentration [17]. The fundamental insight of this theory is that while parallel arrangements of anisotropic objects lead to decreased orientational entropy, there is a compensating increase in positional entropy [17]. For chiral liquid crystals, this model provides the basis for understanding how molecular shape and excluded volume interactions drive the formation of ordered phases.
McMillan's model extends the Maier-Saupe mean field theory to describe phase transitions from nematic to smectic phases [17]. This model utilizes two order parameters: one describing orientational order and another characterizing positional order [17]. The model predicts that phase transitions can be either continuous or discontinuous depending on the strength of short-range intermolecular interactions [17]. For biphenylcarboxylate compounds, this theoretical framework helps explain the temperature-dependent phase sequences observed experimentally.
The elastic continuum theory, also known as Frank theory, treats liquid crystal materials as continua and focuses on perturbations to oriented samples [17]. This formalism identifies three types of distortions: splay, twist, and bend deformations, each associated with specific elastic constants [17]. The elastic response of chiral liquid crystals is particularly important for understanding how external fields and boundary conditions affect molecular organization [17].
The Chiral-Anisotropic Ginzburg-Landau model specifically addresses chiral nematic liquid crystals near winding and unwinding transitions [8]. This model incorporates a complex order parameter and accounts for chirality effects through specific coupling terms [8]. The model has been successful in explaining the formation of branching patterns and chiral bubble structures observed in confined chiral liquid crystals [8].
Advanced computational approaches, including molecular dynamics simulations, have emerged as powerful tools for accelerating the study of liquid crystalline phase transitions [25] [26]. These methods can predict phase sequences, transition temperatures, and local molecular structures through atomistic-level modeling [26]. For complex molecules like (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate, molecular dynamics simulations provide insights into the molecular-level mechanisms governing phase behavior [25].
| Theoretical Model | Primary Application | Key Parameters | Predictive Capability |
|---|---|---|---|
| Onsager Hard-Rod Model | Predicts lyotropic phase transitions based on excluded volume effects | Excluded volume, cylinder orientation, positional entropy | Concentration-dependent phase transitions, nematic phase formation |
| McMillan Model | Describes nematic to smectic A phase transitions with orientational and positional order parameters | Orientational order S, positional order σ, interaction strength α | Continuous vs discontinuous transitions, triple critical points |
| Elastic Continuum Theory (Frank Theory) | Models elastic distortions in liquid crystals using splay, twist, and bend deformations | Elastic constants K₁ (splay), K₂ (twist), K₃ (bend) | Elastic response, boundary conditions, device properties |
| Maier-Saupe Mean Field Theory | Describes phase transitions in nematic liquid crystals using orientational order parameter | Order parameter S, temperature-dependent interactions | Phase transition temperatures, orientational ordering |
| Chiral-Anisotropic Ginzburg-Landau Model | Models chiral nematic liquid crystals near winding/unwinding transitions | Complex order parameter A, chirality parameter χ, elastic coupling δ | Branching patterns, chiral bubble formation, tip-splitting |
| Two-Phase Thermodynamic Model | Analyzes translational, rotational, and vibrational contributions to thermodynamic properties | Translational, rotational, vibrational density of states | Absolute thermodynamic parameters, diffusion anisotropy |
| Molecular Dynamics Approach | Accelerates simulation of liquid crystalline phase transitions | Intermolecular interactions, temperature scaling factors | Phase transition acceleration, mesophase formation dynamics |
Stereochemistry and Chiral Induction in Biphenylcarboxylate Derivatives
The stereochemical aspects of biphenylcarboxylate derivatives like (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate are fundamental to understanding their chiral liquid crystalline behavior [12] [16]. The mechanism of chiral induction involves complex interactions between the chiral center and the biphenyl core, leading to preferred molecular conformations that propagate into macroscopic chiral phases.
Central-to-axial chirality transfer represents the primary mechanism by which chiral centers in biphenylcarboxylate derivatives induce preferred conformations in the biphenyl moiety [16]. Due to the relatively low rotational barrier of approximately 14 kilocalories per mole in biphenyl systems, a thermodynamic equilibrium exists between different diastereoisomers at room temperature [16]. The most stable conformer becomes the predominant species, with the chiral center directing the biphenyl torsion angle [16].
Research has demonstrated that in dioxolanes derived from syn (R,R) 1,2-, 1,3-, or 1,4-chiral diols, the most stable diastereoisomer consistently exhibits an M torsion of the biphenyl moiety [16]. This occurs because in the (R,R,P) isomer, both benzylic methylene groups face bulky R substituents, while in the (R,R,M) configuration, these groups are positioned opposite to hydrogen atoms, resulting in reduced steric interactions [16]. This fundamental relationship provides a predictable framework for understanding chirality transfer in biphenylcarboxylate systems.
The stereochemical configuration has profound effects on the mesophase behavior of these compounds [14]. Computational studies reveal that stereochemical errors, such as incorrect chirality at key centers, can dramatically alter secondary structure and molecular packing [14]. In peptide systems, a flip in chirality can introduce kinks of nearly 90 degrees into helical structures, while maintaining helical character in the segments separated by the distortion [14].
Electronic circular dichroism spectroscopy provides a powerful tool for characterizing chiral induction in biphenylcarboxylate derivatives [16]. The sign of the Cotton effect at 250 nanometers, corresponding to the biphenyl A band absorption, directly indicates the sense of biphenyl twist [16]. A positive Cotton effect corresponds to M torsion, while a negative effect indicates P torsion [16]. This relationship enables rapid determination of absolute configuration without requiring extensive structural analysis.
The propagation of chirality in oligomeric systems demonstrates remarkable amplification effects [12]. Studies of oligopeptides containing biphenyl-based residues show that chiral induction can propagate through multiple residues, creating extended helical structures with enhanced optical activity [12]. This phenomenon is particularly relevant for understanding how local stereochemical features in molecules like (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate can influence bulk liquid crystalline properties.
Conformational preferences play a crucial role in determining the overall molecular shape and packing behavior [34]. Raman spectroscopic studies of related biphenylcarboxylate compounds reveal that phase transitions are accompanied by changes in the dihedral angle between benzene rings [34]. These conformational changes occur discontinuously at phase transition temperatures and are directly related to the smectic polymorphism observed in these materials [34].
| Induction Mechanism | Molecular Basis | Stereochemical Outcome | Detection Method | Design Implications |
|---|---|---|---|---|
| Central-to-Axial Chirality Transfer | Chiral center induces preferred biphenyl torsion (M or P) | M torsion from (R,R) configuration, P from (S,S) | Electronic CD at 250 nm (biphenyl A band) | Predictable chirality transfer rules |
| Conformational Preference | Bulky substituents favor specific conformational states | Extended vs bent molecular conformations | Nuclear magnetic resonance coupling constants, Nuclear Overhauser Effect measurements | Conformational control through substitution |
| Steric Interaction Control | Side chain interactions minimize unfavorable contacts | Reduced steric clashes in preferred arrangements | X-ray crystallography, molecular modeling | Steric bulk optimization for desired phases |
| Hydrogen Bonding Networks | Directional bonding creates ordered arrangements | Helical or layered chiral structures | Vibrational circular dichroism, polarized spectroscopy | Hydrogen bond donor/acceptor positioning |
| π-π Stacking Arrangements | Aromatic ring overlap patterns depend on chirality | Chiral columnar or twisted arrangements | X-ray diffraction, atomic force microscopy imaging | Aromatic core design for chiral stacking |
| Supramolecular Assembly | Non-covalent interactions organize chiral architectures | Hierarchical chiral organization | Circular dichroism, optical rotation | Building block selection for assembly |
Structure–Function Relationships in Liquid Crystal Mesogens
The structure-function relationships in liquid crystal mesogens like (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate are governed by the intricate balance between molecular shape, intermolecular interactions, and thermodynamic factors [13] [21] [24]. Understanding these relationships is essential for predicting and designing materials with specific mesomorphic properties.
The biphenyl core rigidity represents a fundamental structural feature that enhances nematic ordering and maintains molecular anisotropy [13] [21]. Rod-shaped molecules require an extended conformation maintained through the rigidity and linearity of their constituents [13]. The biphenyl system provides this rigidity through its aromatic framework, while the interconnecting groups restrict rotational freedom [13]. This structural constraint is essential for maintaining the anisotropic shape necessary for liquid crystalline behavior.
Molecular anisotropy, characterized by the length-to-width ratio, fundamentally determines the type of mesophase exhibited by a compound [27]. Computer simulations of hard cut spheres, serving as models for disklike mesogens, demonstrate that phase behavior is strongly dependent on the length-to-width ratio [27]. For rod-like molecules like biphenylcarboxylates, the elongated geometry allows for preferential alignment along one spatial direction, promoting calamitic liquid crystalline phases [13].
The chiral center configuration profoundly influences mesophase properties through its effects on molecular packing and helical pitch [32] [35]. Studies of highly chiral biphenylcarboxylate compounds demonstrate continuous supercritical evolution from isotropic phases to blue phases, with the transition characteristics dependent on chiral mole fraction [32]. The stereochemical configuration also affects the stability of specific mesophases, with certain configurations favoring antiferroelectric or anticlinic phases [33].
Alkyl chain length and branching significantly modulate mesophase behavior through their effects on molecular flexibility and packing efficiency [20] [33]. Research on biphenylcarboxylate homologues reveals that lateral alkyl chain length affects smectic layer thickness, indicating that these chains contribute to the molecular long axis dimension [33]. Terminal branching can stabilize smectic phases by filling void spaces in tilted lamellar structures, offsetting the dilution of lateral interactions between mesogenic cores [36].
The jacketing effect observed in mesogen-jacketed liquid crystalline polymers provides insights into how steric hindrance influences molecular conformation [21]. Densely packed side chains force the polymer backbone into extended-chain conformations, directly affecting the resulting mesophase structure [21]. This principle applies to small molecule mesogens where bulky substituents can similarly influence molecular shape and packing.
Linking group flexibility represents another critical design parameter [20]. The incorporation of flexible spacers, such as siloxane units, can decouple the motions of different molecular segments, allowing for almost independent behavior of rigid and flexible components [20]. This decoupling effect is particularly important for achieving desired mesophase properties while maintaining processability.
Aromatic substitution patterns influence electronic properties and intermolecular interactions [35]. Studies of chiral π-conjugated liquid crystals demonstrate that ethynyl linkers and terminal substitution can dramatically affect mesophase stability and spectral properties [35]. The substitution pattern affects not only the molecular shape but also the electronic distribution, influencing π-π stacking interactions and overall mesophase stability.
| Molecular Feature | Effect on Mesophase | Thermodynamic Impact | Molecular Packing |
|---|---|---|---|
| Biphenyl Core Rigidity | Enhances nematic order, maintains molecular rigidity | Increases clearing temperatures, enhances thermal stability | Promotes parallel alignment, reduces conformational freedom |
| Chiral Center Configuration | Induces cholesteric phases, controls helical pitch | Reduces symmetry, creates temperature-dependent pitch | Creates helical arrangements, induces axial chirality |
| Alkyl Chain Length | Modulates layer spacing, affects transition temperatures | Influences entropy-enthalpy balance in phase transitions | Determines layer thickness, affects interdigitation |
| Terminal Branching | Stabilizes smectic phases, fills void spaces in tilted structures | Increases melting point, enhances packing efficiency | Optimizes space filling, reduces void volume |
| Lateral Substitution | Disrupts packing, may destabilize liquid crystalline phases | Generally reduces transition temperatures | Introduces steric hindrance, disrupts regular packing |
| Linking Group Type | Controls molecular flexibility, affects phase sequence | Affects rotational barriers, influences dynamic properties | Controls backbone flexibility, affects chain conformations |
| Aromatic Ring Substitution | Alters electronic properties, influences intermolecular interactions | Modifies dipole moments, affects electrostatic interactions | Influences π-π stacking, affects aromatic interactions |
| Molecular Anisotropy Ratio | Determines phase type (calamitic vs discotic behavior) | Controls excluded volume effects, determines phase boundaries | Governs orientational and positional ordering tendencies |
Molecular Packing and Supramolecular Organization Theories
The molecular packing and supramolecular organization of compounds like (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate involve multiple hierarchical levels of structure, from individual molecular conformations to macroscopic mesophase organization [9] [10] [11]. Understanding these organizational principles is crucial for predicting bulk properties and designing functional materials.
Molecular packing theories are fundamentally based on hard-core repulsion and shape anisotropy effects [22] [27]. The excluded volume model provides the theoretical foundation for understanding how molecular shape influences phase behavior [22]. For anisotropic particles, large excluded volumes restrict particle movement at high concentrations, leading to entropic loss [22]. The system can achieve thermodynamic stabilization through partial orientational ordering, which increases the total entropy by recovering excluded volume for some particles while maintaining translational freedom [22].
Supramolecular assembly in liquid crystalline systems involves the spontaneous organization of molecules through non-covalent interactions [9] [10]. Hydrogen bonding represents a particularly important mechanism for controlling supramolecular organization in liquid crystalline materials [9]. These interactions can be designed to be chemically responsive (pH-responsive) or dynamically structural (temperature-responsive), enabling the creation of stimuli-responsive materials [9].
The self-assembly process in liquid crystals involves the formation of organized, discrete assemblies as well as collective behavior of molecular ensembles [10]. Recognition-induced generation of supramolecular liquid crystals occurs through the formation of specific molecular complexes [10] [15]. For example, trimeric supramolecular disks can self-organize into columnar discotic mesophases through lactim-lactam hydrogen bonding [15].
Phase transition dynamics in chiral liquid crystals involve complex nucleation and growth mechanisms [8] [23]. Molecular dynamics simulations reveal that oscillatory shear can both accelerate and suppress mesophase formation depending on the amplitude [23]. Small amplitude shear accelerates mesophase transition dynamics and results in more ordered mesomorphic structures, while large amplitude shear can destabilize mesophases [23].
The elastic properties of liquid crystalline materials are governed by Frank elastic constants, which describe the energy cost of splay, twist, and bend deformations [17] [37]. These elastic constants can be predicted from molecular simulations, providing a direct link between molecular structure and macroscopic mechanical properties [37]. For biphenylcarboxylate compounds, the elastic response is particularly important for understanding how the material responds to external fields and confinement effects.
Thermal behavior in liquid crystalline systems reflects the competition between entropy and enthalpy contributions [19] [24]. The two-phase thermodynamic model provides a framework for analyzing translational, rotational, and vibrational contributions to thermodynamic properties [19]. During phase transitions, different molecular motions contribute differently to the free energy, with rotational motion dominating in some transitions while translational motion dominates in others [19].
Amphiphilic liquid crystal formation represents another important organizational principle [24]. Molecules containing both hydrophilic and lipophilic components can form amphiphilic liquid crystals through microphase separation [24]. This separation occurs because incompatible molecular segments cannot separate macroscopically but instead organize into microscopically separated layers or other ordered structures [24].
The concept of mesogen-jacketed liquid crystalline polymers illustrates how molecular design can control supramolecular organization [21]. The jacketing effect, where densely packed side chains force extended backbone conformations, demonstrates how local molecular interactions can influence global molecular shape and assembly [21]. This principle applies to small molecule systems where similar steric effects can direct molecular organization.
| Organization Level | Theoretical Framework | Key Principles | Predictive Models | Experimental Validation |
|---|---|---|---|---|
| Molecular Packing | Hard-core repulsion, shape anisotropy effects | Excluded volume optimization, parallel alignment | Density functional theory, Monte Carlo simulations | X-ray diffraction, neutron scattering |
| Supramolecular Assembly | Hydrogen bonding, π-π interactions, van der Waals forces | Recognition-induced assembly, complementary interactions | Molecular dynamics, coarse-grained modeling | Atomic force microscopy, scanning tunneling microscopy |
| Mesophase Structure | Orientational and positional order parameters | Symmetry breaking, long-range order development | Landau-de Gennes theory, order parameter analysis | Polarized optical microscopy, differential scanning calorimetry |
| Phase Transition Dynamics | Nucleation and growth mechanisms, critical phenomena | Critical point behavior, scaling laws | Ginzburg-Landau equations, phase field methods | Time-resolved spectroscopy, dynamic light scattering |
| Elastic Properties | Frank elastic constants, mechanical response | Deformation energy minimization, director distortions | Continuum mechanics, finite element analysis | Mechanical testing, rheological measurements |
| Thermal Behavior | Entropy-enthalpy competition, thermal fluctuations | Temperature-dependent order parameter evolution | Statistical mechanics, thermodynamic modeling | Temperature-dependent property measurements |
The asymmetric synthesis of chiral biphenyl esters represents a cornerstone in the preparation of (S)-4-[(1-Methylheptyloxy)carbonyl]phenyl 4'-octyloxy-4-biphenylcarboxylate and related compounds. Several sophisticated methodologies have been developed to achieve high enantiomeric purity and synthetic efficiency.
The ester-assisted nucleophilic aromatic substitution approach has emerged as a particularly effective strategy for creating axially chiral biphenyl systems [2]. This methodology involves the treatment of 2-tert-butylphenyl 2-[(-)-menthoxy]benzoates with aryl Grignard reagents, where the chirality of the leaving (-)-menthoxy group is transferred to the newly formed biphenyl linkage with up to 94% optical yield . The practical significance of this approach lies in its ability to generate chirality directly during the bond-forming process, eliminating the need for subsequent resolution steps.
Palladium-catalyzed enantioselective C-H arylation has shown remarkable promise in the synthesis of lower carbohelicenes and related biphenyl structures [3]. The use of unique bifunctional phosphine-carboxylate ligands enables the direct catalytic enantioselective synthesis with enantiomeric ratios reaching 98:2 [3]. This methodology demonstrates exceptional versatility across a broad range of substrates, with yields consistently ranging from 84% to 95% while maintaining excellent enantioselectivity.
The development of axially chiral biphenyl ligands through central-to-axial chirality transfer represents another significant advancement [4] [5]. This approach utilizes asymmetric intramolecular Ullmann coupling or iron(III)-promoted oxidative coupling to achieve complete atropdiastereoselectivity. The resulting C2-symmetric biphenyl phosphine ligands can be obtained without requiring optical resolution steps, making this methodology particularly attractive for large-scale applications.
Organocatalytic methods have gained considerable attention for their ability to operate under mild conditions while achieving exceptional enantioselectivity [6]. The use of chiral bifunctional biphenyl-2-ylphosphine ligands in copper-catalyzed transformations has yielded products with enantiomeric excess values exceeding 96% [6]. These systems demonstrate the power of metal-ligand cooperative catalysis in achieving high levels of stereocontrol.
Multi-Step Organic Synthesis Techniques: Strategic Considerations
The synthesis of complex chiral biphenyl esters necessitates careful strategic planning to optimize both synthetic efficiency and stereochemical fidelity. Multi-step synthesis approaches require consideration of reaction sequence, protecting group strategies, and compatibility of reaction conditions.
Sequential coupling strategies represent a fundamental approach to constructing the biphenyl framework [7] [8]. The initial formation of the biphenyl core through iron(III)-catalyzed oxidative coupling provides a robust foundation for subsequent functionalization. This biomimetic approach utilizes iron(III) chloride on silica to achieve 60% yields of biphenyl esters [7]. The reaction mechanism builds on mesomeric effects arising from ortho substitution with electron-donating hydroxyl groups, where iron(III) chloride acts as both catalyst and oxidant.
The strategic implementation of protecting group chemistry plays a crucial role in multi-step synthesis [9]. The synthesis of 4'-bromomethylbiphenyl-2-carboxylates demonstrates effective use of ester protection during bromination reactions [9]. The process involves hydrolysis of 4'-methyl-2-cyanobiphenyl to obtain the corresponding carboxylic acid, followed by esterification using dicyclohexylcarbodiimide (DCC) and 4-dimethylaminopyridine (DMAP) to yield the methyl ester in 98% yield [9].
Enzymatic approaches offer environmentally benign alternatives for selective transformations [7] [10]. Lipase-catalyzed chemoselective ester hydrolysis enables the synthesis of unsymmetric biphenyl-based esters under mild conditions. The optimization of reaction parameters including temperature, pH, and organic solvent content allows for precise control over the chemoselectivity ratio between unsymmetric and symmetric products [7].
The integration of flow chemistry principles has shown promise for optimizing multi-step synthesis [11] [12]. Continuous flow reactors enable precise control over reaction parameters including temperature, residence time, and reagent stoichiometry. This approach has been successfully applied to complex multi-step transformations with improved reproducibility and scalability.
Optimization of Yield and Enantiomeric Purity: Methodological Advances
The optimization of synthetic processes for chiral biphenyl esters requires systematic investigation of reaction parameters to achieve maximum yield while maintaining high enantiomeric purity. Recent advances in optimization methodologies have provided powerful tools for achieving these dual objectives.
Design of Experiments (DoE) approaches have revolutionized the optimization of synthetic processes [13] [12]. The application of face-centered central composite designs enables comprehensive investigation of multiple variables simultaneously. Temperature, catalyst loading, reaction time, and solvent composition represent critical factors that significantly impact both yield and selectivity. Statistical analysis of experimental data provides quantitative models for predicting optimal reaction conditions.
Temperature optimization studies have revealed complex relationships between reaction conditions and product distribution [14] [15]. For biphenyl-2-carboxylic acid decomposition, increasing temperature from 340°C to 400°C resulted in improved selectivity toward ring-opened products, with the biphenyl to fluorenone ratio increasing from 0.43:1 to 0.70:1 [14]. These findings demonstrate the importance of precise temperature control in achieving desired product profiles.
Catalyst loading optimization represents another critical parameter requiring careful consideration [15]. Kinetic analysis of esterification processes has shown that catalyst concentrations follow less than first-order kinetics, suggesting partitioning between catalytically active species and inactive higher-order forms [15]. The optimal catalyst loading of 0.02 M for zirconocene triflate in esterification reactions provides turnover frequencies of approximately 3.3 h⁻¹ [15].
Solvent selection and optimization have proven crucial for achieving high enantioselectivity [8] [16]. The use of water-ethanol mixtures (1:1) in Suzuki-Miyaura cross-coupling reactions has shown superior performance compared to purely organic solvents, achieving yields up to 93% for biphenyl derivatives [8]. The choice of solvent affects not only reaction rates but also the selectivity of stereochemical outcomes.
High-throughput experimentation has become instrumental in expediting optimization processes [17]. The development of automated systems combining synthesis robots, supercritical fluid chromatography, and Bayesian optimization enables efficient exploration of vast parameter spaces. Recent implementations have achieved autonomous optimization across 192 reaction conditions, ultimately enhancing product yields to 49% through systematic parameter adjustment [18].
Comparative Analysis of Synthetic Routes in Literature
A comprehensive evaluation of synthetic methodologies for chiral biphenyl ester preparation reveals significant variations in efficiency, selectivity, and practical applicability. The comparative analysis of different approaches provides essential guidance for selecting optimal synthetic strategies.
The Suzuki-Miyaura cross-coupling methodology consistently demonstrates high yields ranging from 82% to 99% across diverse substrate combinations [19] [8]. The use of nickel ferrite-supported catalysts enables efficient coupling under ultrasonic irradiation, achieving reaction times as short as 25 minutes while maintaining excellent yields [8]. The methodology shows particular strength in its broad substrate tolerance and scalability, making it highly suitable for industrial applications.
Asymmetric C-H arylation approaches exhibit superior selectivity scores, with enantiomeric ratios reaching 98:2 [3]. The use of chiral phosphine-carboxylate ligands enables highly enantioselective synthesis of lower carbohelicenes and related biphenyl structures. While this methodology requires more specialized conditions and catalysts, it provides unmatched stereochemical control for applications requiring high enantiomeric purity.
Enzymatic resolution methods offer exceptional environmental compatibility while achieving good selectivity [7] [10]. The use of lipases from various sources including Candida rugosa, Mucor miehei, and Pseudomonas fluorescens enables chemoselective ester hydrolysis under mild conditions. The optimization of reaction parameters including temperature and dimethyl sulfoxide content allows for preferential formation of unsymmetric products with yields up to 48% after 48 hours [7].
Cost-effectiveness analysis reveals that organocatalytic methods provide the most balanced performance across multiple criteria [20]. These approaches typically require lower catalyst loadings and operate under milder conditions compared to transition metal-catalyzed systems. The development of proline-derived organocatalysts has enabled asymmetric synthesis with enantiomeric excess values exceeding 99% while maintaining reasonable reaction times and yields [21].
Recent advances in mechanochemical synthesis have opened new possibilities for environmentally sustainable biphenyl preparation [22]. Ball milling techniques enable solid-state reactions without requiring organic solvents, achieving modest to good yields while significantly reducing environmental impact. This approach represents a promising direction for green chemistry applications in biphenyl synthesis.