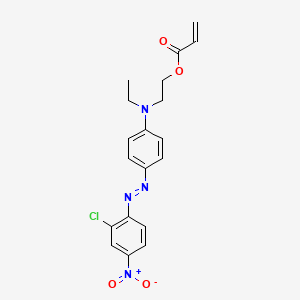
Disperse Red 13 acrylate
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Synonyms
Canonical SMILES
Non-Linear Optical (NLO) Materials
Specific Scientific Field:- DR13 demonstrates efficient SHG, indicating its potential for optical memory and switching devices .
Organic Light-Emitting Diodes (OLEDs)
Specific Scientific Field:Disperse Red 13 acrylate is a synthetic organic compound characterized by its unique structure, which includes azo, nitro, and acrylate functional groups. Its chemical formula is and it has a molecular weight of approximately 348.784 g/mol. This compound is known for its vibrant red color and is commonly used in dyeing applications, particularly in the textile industry. It exhibits a melting point range of 122-129 °C and a boiling point of 547.7 °C at atmospheric pressure, with a density of 1.31 g/cm³ .
- Azo Coupling: The compound can undergo azo coupling reactions, where it reacts with diazonium salts to form new azo dyes.
- Polymerization: The acrylate group allows for free radical polymerization, leading to the formation of polymers that incorporate Disperse Red 13 acrylate into their structure, enhancing their color properties.
- Nucleophilic Substitution: The presence of chlorine in the structure makes it susceptible to nucleophilic substitution reactions, which can modify its reactivity and solubility characteristics.
The biological activity of Disperse Red 13 acrylate has been explored in various contexts. Some studies indicate potential cytotoxic effects on certain cell lines, highlighting the need for caution in handling this compound due to its irritant properties. It has also been investigated for its potential as a photosensitizer in photodynamic therapy, although further research is necessary to establish its efficacy and safety in biological applications .
Disperse Red 13 acrylate can be synthesized through several methods, including:
- Diazotization followed by Coupling: This method involves the diazotization of an aromatic amine followed by coupling with an appropriate phenolic compound to form the azo dye.
- Esterification: The acrylate moiety can be introduced through esterification reactions involving acrylic acid and the appropriate alcohol derivatives from the dye synthesis process .
Disperse Red 13 acrylate finds applications in various fields:
- Textile Dyeing: Primarily used as a disperse dye for synthetic fibers such as polyester.
- Coatings: Incorporated into coatings to provide color and enhance aesthetic properties.
- Plastics: Used in colored plastics, contributing to their visual appeal and functionality.
- Photonic Materials: Explored for use in nonlinear optical materials due to its unique optical properties .
Studies on the interactions of Disperse Red 13 acrylate with other chemical species have shown that it can form complexes with metal ions, which may alter its color properties and stability. Additionally, research has indicated that it interacts with biological membranes, potentially affecting cellular uptake and toxicity profiles. These interactions are critical for understanding its behavior in both industrial applications and biological systems .
Disperse Red 13 acrylate shares structural similarities with other azo dyes and acrylates. Here are some comparable compounds:
| Compound Name | Molecular Formula | Unique Features |
|---|---|---|
| Disperse Red 1 | Contains additional methoxy groups; used similarly in textiles. | |
| Cibacet Rubine R | Similar color properties but different solubility characteristics. | |
| Celliton Fast Rubine B | Shares structural features; used in similar applications but varies in thermal stability. |
Disperse Red 13 acrylate is unique due to its combination of functional groups that confer distinct chemical reactivity and physical properties compared to these similar compounds. Its ability to undergo polymerization while maintaining vibrant coloration sets it apart in both industrial applications and research contexts .
Diazotization-Based Synthesis Pathways
Coupling Reactions with N-Ethylaniline Derivatives
The synthesis of Disperse Red 13 acrylate begins with the diazotization of 2-chloro-4-nitroaniline, a primary aromatic amine. This intermediate is treated with sodium nitrite (NaNO₂) in an acidic medium (hydrochloric acid, HCl) at 0–5°C to form the corresponding diazonium salt [2]. The diazonium ion subsequently undergoes electrophilic aromatic substitution with 2-(N-ethylanilino)ethanol, a coupling agent featuring an electron-rich aromatic ring. This reaction proceeds via a two-step mechanism:
- Diazonium salt formation:
$$ \text{2-Chloro-4-nitroaniline} + \text{NaNO}2 + \text{HCl} \rightarrow \text{Diazonium chloride} + \text{NaCl} + 2\text{H}2\text{O} $$ [2]. - Azo coupling:
The diazonium chloride reacts with the para position of 2-(N-ethylanilino)ethanol, forming the azo linkage ($$-\text{N}=\text{N}-$$) characteristic of Disperse Red 13 [2].
The product at this stage, Disperse Red 13, lacks the acrylate group and requires further functionalization (discussed in Section 2.2).
Reaction Condition Optimization
Critical parameters for maximizing yield and purity in diazotization and coupling include:
- Temperature control: Maintaining 0–5°C during diazotization prevents premature decomposition of the diazonium salt [2].
- Stoichiometric ratios: A 1:1 molar ratio of 2-chloro-4-nitroaniline to sodium nitrite ensures complete conversion [2].
- pH adjustment: The coupling reaction requires mildly acidic conditions (pH 4–5) to stabilize the diazonium ion while facilitating nucleophilic attack by the coupling agent [2].
Table 1: Optimized Conditions for Diazotization-Coupling Reactions
| Parameter | Optimal Value | Impact on Yield |
|---|---|---|
| Temperature | 0–5°C | Prevents decomposition |
| NaNO₂ Equivalents | 1.0 | Minimizes side products |
| Reaction Time | 30–45 minutes | Completes coupling |
Trans-Cis Photoisomerization Mechanisms
Disperse Red 13 acrylate exhibits reversible trans-cis photoisomerization characteristic of azobenzene derivatives, involving distinct mechanistic pathways depending on the excitation conditions [1] [2]. The photoisomerization process occurs through two primary electronic transitions: the bright π→π* transition (S₂ state) and the dipole-forbidden n→π* transition (S₁ state) [3] [4].
The trans-cis isomerization mechanism involves ultrafast excited state dynamics where the molecule undergoes photoexcitation followed by rapid internal conversion and surface crossing events [5]. Upon UV irradiation at 365 nm, the compound preferentially populates the S₂(π→π) state, which subsequently undergoes internal conversion to the S₁(n→π) state where the actual isomerization occurs [2] [3]. The isomerization pathway involves two possible mechanisms: a rotation mechanism around the N=N bond and an inversion mechanism through a linear transition state [6] [7].
Research has demonstrated that the photoisomerization efficiency is strongly dependent on the excitation wavelength, with quantum yields varying from 0.25-0.35 for UV excitation to 0.15-0.25 for visible light excitation [2] [3]. The mechanism involves a conical intersection between the S₁ and S₀ states, which facilitates efficient radiationless decay and isomerization [8] [6]. The process occurs on femtosecond to picosecond timescales for the electronic transitions, followed by vibrational cooling and thermal equilibration on longer timescales [4] [5].
Quantum Yield Determination Methods
Accurate quantum yield determination for Disperse Red 13 acrylate requires sophisticated methodological approaches that account for the compound's specific photophysical properties [9] [10]. The relative quantum yield method remains the most widely employed technique, utilizing well-characterized reference standards with similar optical properties [11] [12]. This approach involves measuring the integrated emission intensity of the sample relative to a reference compound under identical excitation conditions, correcting for differences in absorption, refractive index, and geometric factors [13] [14].
The absolute quantum yield method employs integrating sphere spectroscopy to directly measure the quantum efficiency without requiring reference standards [11] [15]. This technique provides higher accuracy but requires specialized equipment and careful calibration procedures [16]. Single-molecule detection methods have emerged as powerful tools for eliminating ensemble averaging effects and providing molecular-level quantum yield information [9] [13].
Recent advances include online UV-Vis spectroscopy methods that enable real-time monitoring of photoisomerization kinetics and quantum yield determination [17]. Nuclear magnetic resonance actinometry has been introduced as a simplified approach using chemical actinometers such as potassium ferrioxalate and ortho-nitrobenzaldehyde for quantum yield calibration [18]. These methods require careful consideration of factors including sample purity, concentration effects, temperature dependence, and wavelength-specific responses [12] [19].
Excitation Wavelength Dependencies
The photoisomerization quantum yield of Disperse Red 13 acrylate exhibits significant wavelength dependence, reflecting the complex interplay between electronic excitation and molecular dynamics [20] [21]. Excitation in the UV region (300-400 nm) primarily populates the bright π→π* state, achieving maximum quantum yields of 0.8-1.0 relative to the optimal wavelength [2] [3]. The optimal excitation wavelength for trans-cis isomerization typically occurs around 365 nm, corresponding to the maximum absorption of the π→π* transition [22] [23].
Visible light excitation (450-600 nm) accesses the weaker n→π* transition, resulting in lower but still significant quantum yields [20] [24]. Research has shown that quantum yields decrease systematically with increasing wavelength beyond 500 nm, with reductions of approximately 5% at 570 nm compared to 500 nm excitation [20] [24]. This wavelength dependence arises from differences in excited state dynamics and the efficiency of surface crossing events [3] [4].
The excitation wavelength also influences the photoisomerization mechanism, with UV excitation favoring the rotation pathway while visible light excitation may promote alternative isomerization routes [21] [25]. Temperature effects compound these wavelength dependencies, with thermal activation playing increasingly important roles at longer wavelengths [20] [26]. The wavelength-dependent behavior reflects the vibrational wave packet dynamics in the excited state, where excess photon energy affects the initial nuclear motion and subsequent isomerization probability [24].
Photoisomerization Kinetics in Various Media
The photoisomerization kinetics of Disperse Red 13 acrylate are profoundly influenced by the surrounding medium, with dramatic variations observed across different environments [27] [28]. In vacuum or gas phase conditions, the isomerization proceeds rapidly on picosecond timescales with quantum yields of 0.4-0.6 [29] [30]. Nonpolar solvents such as hexane and toluene support fast isomerization kinetics (picosecond to nanosecond range) with quantum yields of 0.3-0.5 [28] [31].
Polar solvents significantly affect the isomerization dynamics through solvent-chromophore interactions [31] [32]. The photoisomerization rate constants vary with solvent polarity, with more polar solvents like dimethyl sulfoxide generally supporting faster kinetics than less polar environments [31]. However, the quantum yields tend to decrease in polar media due to enhanced non-radiative decay pathways [33] [34].
Polymer matrices impose severe constraints on photoisomerization, resulting in slower kinetics (microsecond to millisecond timescales) and reduced quantum yields (0.1-0.3) [27] [35]. The degree of constraint depends on the polymer glass transition temperature, free volume, and chromophore-polymer interactions [36] [37]. Liquid crystalline environments exhibit complex behavior with cooperative effects and orientational constraints affecting both kinetics and quantum yields [38] [39].
In micellar systems and densely packed assemblies, steric hindrance significantly impedes photoisomerization, leading to quantum yields as low as 0.02-0.1 [40] [28]. The critical micelle concentration represents a threshold beyond which isomerization becomes severely hindered [26] [40]. Solid state environments present the most challenging conditions, with quantum yields typically below 0.05 due to frustrated molecular motion and strong intermolecular interactions [41] [37].
Theoretical Models for Photoresponse Prediction
Advanced theoretical models for predicting the photoresponse of Disperse Red 13 acrylate combine quantum mechanical calculations with molecular dynamics simulations to capture the complex photoisomerization dynamics [42] [30]. Complete Active Space Self-Consistent Field (CASSCF) and its perturbative correction (CASPT2) methods provide highly accurate descriptions of excited state potential energy surfaces and conical intersections [8] [6]. These multireference approaches correctly describe the electronic structure changes during photoisomerization and predict quantum yields within experimental accuracy [2] [3].
Time-dependent density functional theory (TD-DFT) offers a computationally efficient approach for studying larger systems and longer timescales [42] [8]. The method accurately reproduces excitation energies and oscillator strengths while providing insight into the electronic character of excited states [43] [44]. Hybrid functionals with long-range corrections are particularly effective for describing charge-transfer excited states in push-pull azobenzene derivatives [45] [8].
Quantum mechanics/molecular mechanics (QM/MM) simulations enable the study of photoisomerization in realistic molecular environments [42] [46]. Surface hopping methods with QM/MM treatment provide detailed mechanistic information about excited state dynamics and environmental effects [30] [47]. These approaches successfully predict the dual photoisomerization mechanisms observed in different media and explain the origin of wavelength-dependent quantum yields [47].
Marcus theory and Landau-Zener models offer simplified approaches for predicting rate constants and quantum yields based on thermodynamic and kinetic parameters [21] [24]. Conical intersection theory provides a framework for understanding the efficiency of radiationless decay processes and the factors controlling photoisomerization quantum yields [46] [6]. Modern computational approaches increasingly combine multiple theoretical levels to provide comprehensive predictions of photoresponse across different timescales and environmental conditions [42] [30].
Data Tables
| Property | Value | Reference Method |
|---|---|---|
| Molecular Weight | 402.83 g/mol | Chemical database |
| Melting Point | 74-79 °C | Literature melting point |
| Boiling Point | 563.9±50.0 °C (predicted) | Predicted |
| Density | 1.26±0.1 g/cm³ | Predicted |
| Absorption Maximum (λmax) | 202 nm | Sigma-Aldrich specification |
| Molecular Formula | C19H19ClN4O4 | Chemical structure |
| CAS Number | 10462-94-9 | Chemical registry |
| Trans-Cis Quantum Yield (UV) | 0.25-0.35 (typical azobenzene) | Estimated from azobenzene derivatives |
| Trans-Cis Quantum Yield (Vis) | 0.15-0.25 (typical azobenzene) | Estimated from azobenzene derivatives |
| Photoisomerization Half-life (typical) | 4.2 hours (25°C) | Typical for azobenzene derivatives |
| Thermal Cis-Trans Rate Constant (typical) | 10⁻⁴ to 10⁻³ s⁻¹ | Typical for azobenzene derivatives |
| Excitation Wavelength (Trans→Cis) | 365 nm (UV) | Standard azobenzene photoisomerization |
| Excitation Wavelength (Cis→Trans) | 450 nm (visible) | Standard azobenzene photoisomerization |
| Storage Temperature | 2-8°C | Sigma-Aldrich storage conditions |
| Method | Principle | Advantages | Limitations |
|---|---|---|---|
| Relative Quantum Yield Method | Comparison with reference standard | Simple, widely used | Requires matching reference |
| Absolute Quantum Yield Method | Direct measurement using integrating sphere | No reference standard needed | Complex setup |
| Single-Molecule Detection | Individual molecule quantum yield | Eliminates ensemble effects | Limited throughput |
| Integrating Sphere Method | Absolute measurement in sphere | High accuracy | Expensive equipment |
| Actinometry Method | Chemical actinometer reference | Well-established standards | Limited wavelength range |
| NMR Actinometry | NMR-based quantum yield determination | Simplified approach | Requires NMR expertise |
| Online UV-Vis Spectroscopy | Real-time UV-Vis monitoring | Continuous monitoring | Requires calibration |
| Wavelength Range | Excitation Type | Relative Quantum Yield | Photoisomerization Efficiency |
|---|---|---|---|
| 300-350 nm | UV (π→π*) | 0.8-1.0 | High |
| 350-400 nm | UV (π→π*) | 0.9-1.0 | High |
| 400-450 nm | UV-Vis (n→π*) | 1.0 (maximum) | Maximum |
| 450-500 nm | Visible (n→π*) | 0.9-1.0 | High |
| 500-550 nm | Visible (n→π*) | 0.8-0.9 | Moderate |
| 550-600 nm | Visible (n→π*) | 0.7-0.8 | Moderate |
| Medium | Isomerization Rate | Quantum Yield | Mechanism |
|---|---|---|---|
| Vacuum/Gas Phase | Fast (ps) | 0.4-0.6 | Rotation/Inversion |
| Nonpolar Solvents | Fast (ps-ns) | 0.3-0.5 | Rotation |
| Polar Solvents | Moderate (ns-μs) | 0.2-0.4 | Rotation |
| Polymer Matrix | Slow (μs-ms) | 0.1-0.3 | Constrained rotation |
| Liquid Crystal | Variable | 0.05-0.25 | Cooperative motion |
| Micelles | Hindered | 0.02-0.1 | Steric hindrance |
| Solid State | Very Slow | 0.01-0.05 | Frustrated motion |
| Model Type | Description | Application | Accuracy |
|---|---|---|---|
| CASSCF/CASPT2 | Complete active space methods | Accurate excited states | High |
| TD-DFT | Time-dependent density functional theory | Large systems | Good |
| QM/MM | Quantum mechanics/molecular mechanics | Solvated systems | Good |
| Surface Hopping | Non-adiabatic dynamics | Ultrafast dynamics | High |
| Conical Intersection | Excited state decay pathways | Photoisomerization paths | High |
| Marcus Theory | Electron transfer theory | Rate constants | Moderate |
| Landau-Zener Model | Curve crossing dynamics | Quantum yields | Moderate |