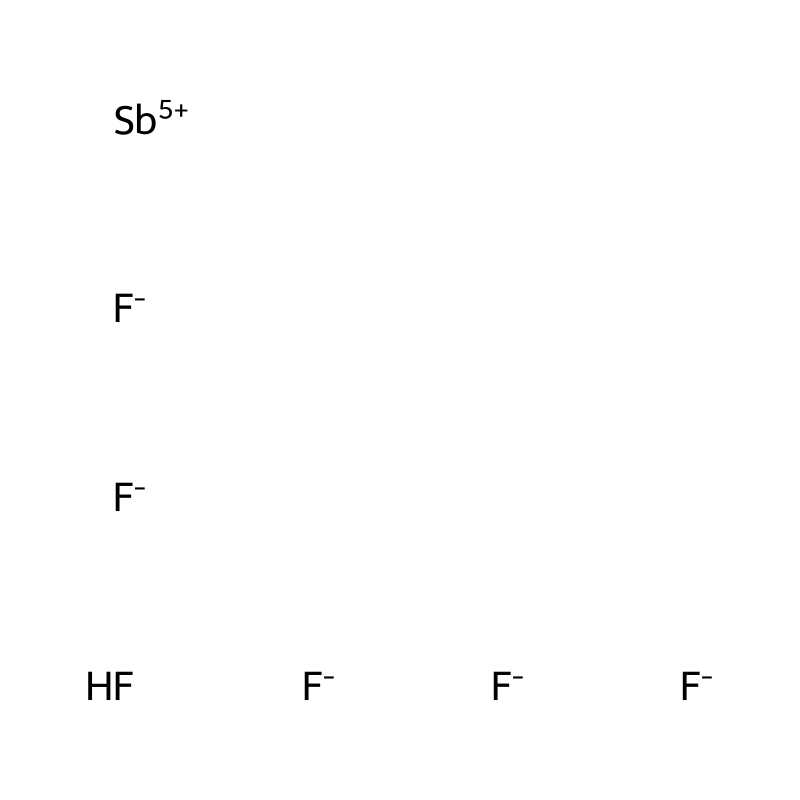
fluoroantimonic acid
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
SMILES
Synthesis of Alkylidene Oxonium Salts
Field: Organic Chemistry
Application: Fluoroantimonic acid is used as a medium for the preparation of alkylidene oxonium salts.
Method: The specific methods of application or experimental procedures would depend on the particular synthesis being performed. Generally, the acid would be carefully added to the reaction mixture containing the precursor compounds.
Results: The outcome is the formation of alkylidene oxonium salts.
Etching of Glass
Field: Materials Science
Application: Fluoroantimonic acid is used to etch glass.
Method: The acid would be applied to the glass surface and allowed to react for a certain period of time. The glass would then be thoroughly rinsed to remove the acid and stop the reaction.
Protonation of Organic Compounds
Application: Fluoroantimonic acid’s unique talent is protonation — it donates protons to organic compounds.
Method: The specific methods of application or experimental procedures would depend on the particular reaction being performed. Generally, the acid would be carefully added to the reaction mixture containing the precursor compounds.
Results: The outcome is the alteration of the compound’s properties.
Catalyst for Alkylations and Acylations in Petrochemistry
Field: Petrochemistry
Application: Fluoroantimonic acid is used as a catalyst for alkylations and acylations in petrochemistry.
Method: The acid would be added to the reaction mixture containing the precursor compounds. The reaction would then be allowed to proceed under controlled conditions.
Results: The result is the formation of alkylated or acylated products.
Fluoroantimonic acid, with the chemical formula H[SbF6], is recognized as the strongest known superacid. It is formed through the reaction of hydrogen fluoride and antimony pentafluoride, resulting in a colorless, crystalline solid that is highly corrosive and reactive. The molecular structure of fluoroantimonic acid features a trigonal bipyramidal geometry with two hydrogen atoms and five fluorine atoms surrounding a central antimony atom. This unique arrangement contributes to its extreme acidity and reactivity, making it a powerful oxidizing and fluorinating agent used in various chemical processes .
Fluoroantimonic acid's extreme acidity stems from its unique ability to generate highly reactive free protons (H+). The surrounding HF molecules stabilize this highly charged species, allowing it to protonate a vast range of compounds by accepting electrons and forming covalent bonds. This protonation process is the foundation of fluoroantimonic acid's role as a superacid catalyst in various organic reactions.
Fluoroantimonic acid is no friend to the careless chemist. Here's why:
The synthesis of fluoroantimonic acid involves several steps:
- Preparation of Ammonium Hexafluoroantimonate:
- Antimony pentafluoride reacts with anhydrous ammonia to form ammonium hexafluoroantimonate:
- Conversion to Fluoroantimonic Acid:
- The ammonium hexafluoroantimonate is treated with concentrated sulfuric acid or fluorosulfonic acid at elevated temperatures:
This process yields fluoroantimonic acid as a colorless, fuming liquid .
Fluoroantimonic acid has several important applications in both organic synthesis and materials science:
- Fluorination Reagent: It is extensively used in organic synthesis for the fluorination of various compounds.
- Catalyst: In chemical processes, fluoroantimonic acid serves as a catalyst due to its strong acidic properties.
- High-Performance Polymers: It facilitates the development of advanced materials such as phosphinated curable polyimides and fluorinated polymers with enhanced properties .
Research on fluoroantimonic acid's interactions focuses on its ability to protonate various organic substrates and its reactivity with metals. Studies have demonstrated that it can effectively protonate hydrocarbons and other organic compounds that are generally resistant to protonation under standard conditions. Furthermore, its interactions with metals highlight its capability to generate hydrogen gas rapidly upon contact
Fluoroantimonic acid stands out among superacids due to its unprecedented strength. Here are some similar compounds for comparison:
| Compound | Chemical Formula | Acidity (Hammett function) | Unique Features |
|---|---|---|---|
| Fluoroantimonic Acid | H[SbF6] | -31 | Strongest known superacid; can protonate methane |
| Magic Acid | H[FSO3] | -14 | Less strong than fluoroantimonic acid; used in organic synthesis |
| Triflic Acid | H[CF3SO3] | -14 | Strong proton donor; used in various
Dates
Modify: 2023-11-23
1. Olah, G. A. (2001). A Life of Magic Chemistry: Autobiographical Reflections of a Nobel Prize Winner. John Wiley and Sons. pp. 100–101. ISBN 978-0-471-15743-4.
2. Esteves, Pierre M.; Ramírez-Solís, Alejandro; Mota, Claudio J. A. (March 2002). "The Nature of Superacid Electrophilic Species in HF/SbF5: A Density Functional Theory Study". Journal of the American Chemical Society. 124 (11): 2672–2677. doi:10.1021/ja011151k. ISSN 0002-7863. PMID 11890818. 3. Klein, Michael L. (October 25, 2000). "Getting the Jump on Superacids" (PDF). Pittsburgh Supercomputing Center (PSC). Archived from the original (PDF) on May 31, 2012. Retrieved 2012-04-15. 4. Mootz, Dietrich; Bartmann, Klemens (March 1988). "The Fluoronium Ions H2F+ and H 3F+ 2: Characterization by Crystal Structure Analysis". Angewandte Chemie International Edition. 27 (3): 391–392. doi:10.1002/anie.198803911. 5. Olah, G. A. (2005). "Crossing Conventional Boundaries in Half a Century of Research". Journal of Organic Chemistry. 70 (7): 2413–2429. doi:10.1021/jo040285o. PMID 15787527. 6. Olah estimates that HF-SbF5 may reach H0 values as low as –28. On the other hand, in ref. 1 (2009), Olah cites one method that estimated H0 values down to –27 for FSO3H-SbF5 at 90% SbF5, but indicates that more reliable experimentally determined equilibrium constants do not support H0 values lower than about –24 for either magic acid or fluoroantimonic acid. 7. Gillespie, R. J.; Peel, T. E. (1973-08-01). "Hammett acidity function for some superacid systems. II. Systems sulfuric acid-[fsa], potassium fluorosulfate-[fsa], [fsa]-sulfur trioxide, [fsa]-arsenic pentafluoride, [sfa]-antimony pentafluoride and [fsa]-antimony pentafluoride-sulfur trioxide". Journal of the American Chemical Society. 95 (16): 5173–5178. doi:10.1021/ja00797a013. ISSN 0002-7863. 8. Koppel, Ilmar A.; Burk, Peeter; Koppel, Ivar; Leito, Ivo; Sonoda, Takaaki; Mishima, Masaaki (May 2000). "Gas-Phase Acidities of Some Neutral Brønsted Superacids: A DFT and ab Initio Study". Journal of the American Chemical Society. 122 (21): 5114–5124. doi:10.1021/ja0000753. ISSN 0002-7863. 9. Meyer, Matthew M.; Wang, Xue-bin; Reed, Christopher A.; Wang, Lai-Sheng; Kass, Steven R. (2009-12-23). "Investigating the Weak to Evaluate the Strong: An Experimental Determination of the Electron Binding Energy of Carborane Anions and the Gas phase Acidity of Carborane Acids". Journal of the American Chemical Society. 131 (50): 18050–18051. doi:10.1021/ja908964h. ISSN 0002-7863. PMID 19950932. S2CID 30532320. 10. Oelderik, Jan (December 1966). "Werkwijze ter bereiding van halogeenverbindingen van vijfwaardig antimoon". Netherlands Patent Application. NL 6508096 A. Explore Compound TypesGet ideal chemicals from 750K+ compounds
CAS No.:147568-66-9
Molecular Formula:C21H24N2O4
Molecular Weight:368.4 g/mol
Availability:
In Stock
CAS No.:5516-88-1
Molecular Formula:C16H16N2O2
Molecular Weight:268.31 g/mol
Availability:
In Stock
CAS No.:18910-65-1
Molecular Formula:C19H25NO4
Molecular Weight:331.4 g/mol
Availability:
In Stock
CAS No.:1802706-04-2
Molecular Formula:C27H35F3N4O3S
Molecular Weight:552.7 g/mol
Availability:
In Stock
CAS No.:74923-08-3
Molecular Formula:C9H12N2O3
Molecular Weight:196.2 g/mol
Availability:
In Stock
CAS No.:535-83-1
Molecular Formula:C7H7NO2
Molecular Weight:137.14 g/mol
Availability:
In Stock
CAS No.:136-69-6
Molecular Formula:C18H22ClNO5
Molecular Weight:367.8 g/mol
Availability:
In Stock
CAS No.:2355-31-9
Molecular Formula:C8F17SO2N(CH3)CH2COOH
C11H6F17NO4S
Molecular Weight:571.21 g/mol
Availability:
In Stock
© 2024 Smolecule Inc. All rights reserved.
|
