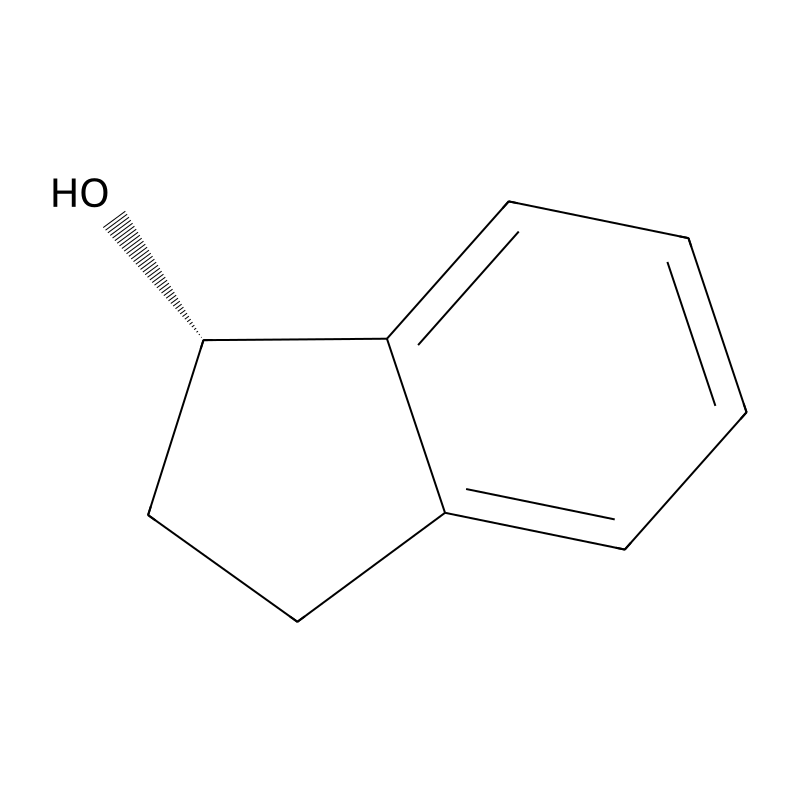
(S)-(+)-1-Indanol

(S)-(+)-1-Indanol (CAS: 25501-32-0) is a rigid, enantiopure bicyclic secondary alcohol that serves as a critical chiral building block in pharmaceutical manufacturing and asymmetric catalysis[1]. Unlike its achiral precursor, 1-indanone, or flexible aliphatic alcohols, the conformationally constrained indane ring of (S)-1-indanol provides a highly effective stereodirecting environment. In industrial procurement, its primary value lies in its high enantiomeric purity (>99% ee), which allows it to be used directly in stereospecific SN2 inversions or as a chiral ligand precursor [2]. By starting with the enantiopure (S)-form, chemists can reliably predict and control the stereochemistry of downstream active pharmaceutical ingredients (APIs) and advanced materials without the need for complex, yield-limiting late-stage resolution.

Attempting to substitute enantiopure (S)-(+)-1-Indanol with racemic 1-indanol or achiral 1-indanone fundamentally undermines process economics and product viability [1]. In pharmaceutical synthesis, such as the production of the Parkinson's drug Rasagiline, using the racemate necessitates a late-stage diastereomeric resolution (e.g., using L-tartaric acid), which mathematically caps the theoretical yield of the desired enantiomer at 50% and generates an equal volume of chemical waste [2]. Furthermore, substituting with the opposite (R)-enantiomer is not an option, as it leads to the formation of the inactive or off-target stereoisomer of the final API. Consequently, procuring the exact (S)-enantiomer is not merely a quality preference; it is a strict requirement to maintain commercial viability, avoid complex preparative chiral chromatography, and ensure the biological efficacy of the end product.

Stereoinversion Yield in API Synthesis

In the synthesis of (R)-Rasagiline, starting with (S)-1-indanol allows for a direct stereoinvertive N-alkylation (e.g., via mesylation and subsequent amine displacement), achieving high isolated yields of the correct API stereoisomer in a streamlined process [1]. Conversely, utilizing racemic 1-indanol or synthesizing from 1-indanone requires the formation of a racemic amine intermediate, which must then undergo diastereomeric resolution. This late-stage resolution limits the theoretical maximum yield to 50% and requires extensive recycling or discarding of the unwanted enantiomer[2].

Procuring the (S)-enantiomer directly eliminates the 50% yield penalty and the operational bottleneck of late-stage chiral resolution in pharmaceutical manufacturing.

Eliminating Chiral Chromatography Costs

When racemic mixtures of 1-indanol are used, separating the (S)- and (R)-enantiomers requires preparative liquid chromatography on specialized chiral stationary phases, such as cellulose tribenzoate[1]. The competitive adsorption isotherms (modeled via Bilangmuir or Toth equations) demonstrate that overloaded elution profiles suffer from significant peak overlap, restricting throughput and consuming massive volumes of high-purity solvents [1]. Procuring >99% ee (S)-1-indanol entirely bypasses this highly capital- and solvent-intensive downstream processing step.

Bypassing preparative chiral chromatography drastically reduces capital expenditure and solvent waste during process scale-up.

Chiral Ligand Stereocontrol

(S)-1-indanol is frequently utilized as a rigid scaffold for the synthesis of chiral ligands, such as indanol-derived oxazaborolidines or phosphine ligands [1]. The enantiomeric purity of the starting alcohol directly translates to the stereodirecting capability of the resulting catalyst. A catalyst derived from enantiopure (S)-1-indanol can drive asymmetric reductions or alkylations with >95% enantiomeric excess (ee)[2]. If a racemic or partially resolved indanol is used, the resulting catalyst mixture will yield a corresponding drop in product ee, rendering the downstream asymmetric transformation useless for fine chemical production.

For manufacturers of chiral catalysts, the enantiopurity of the procured (S)-1-indanol is the sole determinant of the final product's market value and functional performance.

Rasagiline & MAO-B Inhibitor Synthesis

Directly following from its high stereoinvertive yield efficiency, (S)-1-indanol is the optimal starting material for synthesizing (R)-Rasagiline, a critical Parkinson's disease medication. By converting the (S)-hydroxyl group to a leaving group (such as a mesylate) and performing an SN2 displacement with propargylamine, manufacturers achieve the required (R)-stereocenter in high yield while completely avoiding the 50% waste penalty of late-stage racemic resolution [1].

Chiral Ligands for Asymmetric Catalysis

Leveraging its rigid indane framework and defined stereochemistry, (S)-1-indanol is utilized to synthesize high-performance chiral ligands, including oxazaborolidines and specialized phosphine ligands. Procuring the enantiopure (S)-form ensures that the resulting catalysts deliver maximum enantiomeric excess (>95% ee) in downstream asymmetric reductions and carbon-carbon bond-forming reactions [2].

Chiral Intermediates for Antiviral APIs

The strict stereochemical requirements of HIV protease inhibitors, such as Indinavir analogs, rely on the precise spatial arrangement of the indane ring. (S)-1-indanol serves as a reliable, enantiopure building block to construct these complex multi-chiral-center APIs, ensuring that the final drug molecules possess the exact 3D conformation required for optimal biological target binding and therapeutic efficacy [3].