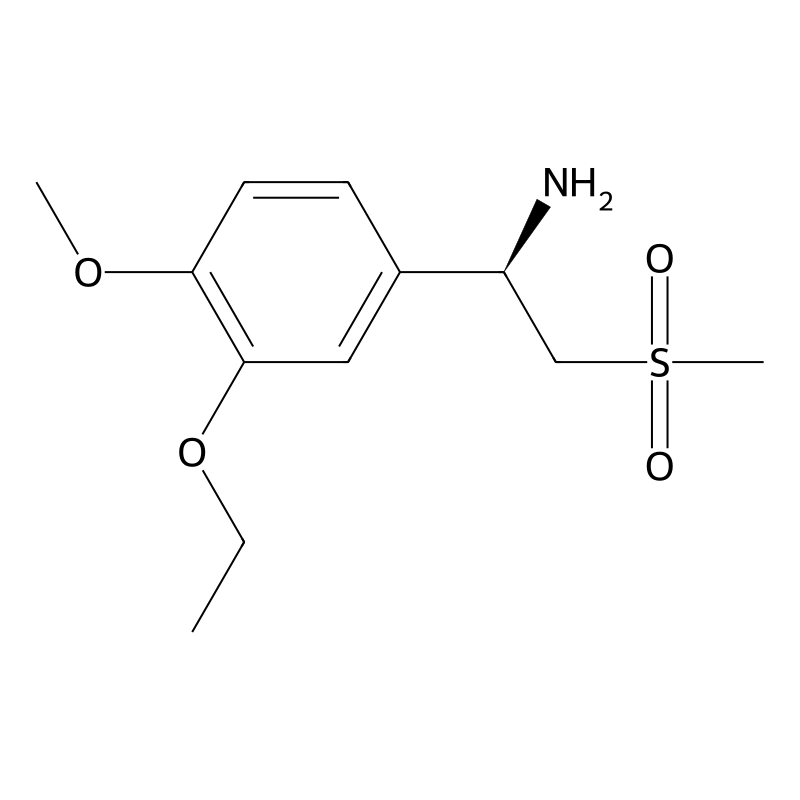
(R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Canonical SMILES
Isomeric SMILES
Synthesis and Characterization:
A few studies have reported the synthesis and characterization of (R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine. These studies describe methods for its preparation and its characterization using various techniques such as nuclear magnetic resonance (NMR) spectroscopy and mass spectrometry [, ].
Potential Applications:
Based on the presence of specific functional groups, the molecule possesses some characteristics that could be relevant for scientific research:
- The presence of a chiral center: The molecule contains a stereocenter, indicated by the "(R)" designation. This chirality could be important for studying the interaction of the molecule with other chiral biological molecules [].
- Functional groups: The molecule contains several functional groups, including an ethoxy group, a methoxy group, a methylsulfonyl group, and an amine group. These groups can potentially interact with various biological targets and participate in different chemical reactions [].
(R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine is a chemical compound with the molecular formula C₁₂H₁₉NO₄S and a molecular weight of 273.35 g/mol. This compound is characterized by its unique structure, which includes a phenyl ring substituted with ethoxy and methoxy groups, and a sulfonyl group attached to an ethanamine moiety. It is primarily known as an impurity in the synthesis of Apremilast, a selective phosphodiesterase 4 inhibitor used in treating inflammatory conditions such as psoriatic arthritis .
The synthesis of (R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine involves several key reactions:
- Nucleophilic Addition: The reaction begins with the nucleophilic addition of a deprotonated dialkylsulfone to an imine formed from a protected amine and an aldehyde derivative .
- Dehydration: Following the addition, dehydration occurs to form an unsaturated intermediate.
- Diastereoselective Addition: This step involves the addition of another nucleophile under controlled conditions to ensure selectivity.
- Deprotection: The final step typically involves deprotecting the amine group to yield the desired aminosulfone product .
(R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine exhibits biological activity primarily through its role as an impurity in Apremilast synthesis. Apremilast itself is known for its ability to inhibit phosphodiesterase 4, leading to decreased production of pro-inflammatory cytokines, making it effective in managing conditions like psoriatic arthritis and Crohn's disease .
The synthesis methods for (R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine include:
- Chiral Resolution: The compound can be synthesized through chiral resolution techniques involving specific amino acid salts to obtain the desired enantiomer .
- Asymmetric Hydrogenation: This method employs catalytic processes to achieve high enantioselectivity during the formation of the sulfonamide linkage .
Interaction studies involving (R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine focus on its pharmacokinetic properties and potential interactions with other drugs. As part of Apremilast, it may interact with various enzymes and transporters involved in drug metabolism, particularly those related to liver function and gastrointestinal absorption .
Several compounds share structural similarities with (R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine, including:
| Compound Name | Structure Features | Biological Activity |
|---|---|---|
| Apremilast | Contains similar phenolic structure; selective phosphodiesterase 4 inhibitor | Treats psoriatic arthritis |
| (S)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine | Enantiomer of (R); similar synthesis method | Exhibits comparable biological effects |
| 1-(3-Ethoxy-4-methoxyphenyl)-2-(methylthio)ethanamine | Similar structure but lacks sulfonyl group | Potentially different biological profile |
The uniqueness of (R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine lies in its specific enantiomeric form and its role as an impurity in Apremilast synthesis, which influences both its chemical behavior and biological activity compared to other similar compounds .
Role in Apremilast Synthesis: Mechanistic Insights
(R)-1-(3-Ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine serves as a pivotal intermediate in the synthesis of apremilast, an oral PDE4 inhibitor approved for psoriasis and psoriatic arthritis. The compound’s (R)-enantiomer is essential for achieving the desired stereochemical configuration of apremilast, which directly influences its binding affinity to PDE4 isoforms [3] [5].
The synthesis pathway involves a multi-step process:
- Formation of the Chiral Center: The ethanamine backbone is functionalized with a methylsulfonyl group, followed by resolution of the (R)-enantiomer using chiral chromatography or asymmetric catalysis [1] [5].
- Coupling with the Phthalimide Moiety: The intermediate undergoes condensation with 3-acetamidophthalic anhydride to form the final apremilast structure. This step is optimized in a one-pot reaction to avoid isolating unstable intermediates, as described in patent US10287248B2 [5].
A critical advancement in apremilast synthesis is the use of acetic anhydride to acetylate the amine group in situ, which prevents side reactions and improves yield [5]. The methylsulfonyl group enhances solubility and stabilizes the intermediate during purification [3].
Table 1: Key Reactions in Apremilast Synthesis Using (R)-1-(3-Ethoxy-4-Methoxyphenyl)-2-(Methylsulfonyl)Ethanamine
| Reaction Step | Reagents/Conditions | Purpose |
|---|---|---|
| Enantiomeric Resolution | Chiral stationary phase | Isolate (R)-enantiomer |
| Methylsulfonation | Methanesulfonyl chloride | Introduce sulfonyl group |
| Phthalimide Coupling | 3-Acetamidophthalic anhydride | Form apremilast backbone |
Structure-Activity Relationship Studies of Ethoxymethoxy Substitutions
The ethoxy and methoxy substituents at the 3- and 4-positions of the phenyl ring are critical for PDE4 inhibition. Structural analyses reveal:
- Methoxy Group at C4: Enhances binding to the hydrophobic pocket of PDE4B/D subtypes through van der Waals interactions [2].
- Ethoxy Group at C3: Introduces steric bulk that improves selectivity for PDE4B over PDE4A, as evidenced by orismilast’s 3.2-fold selectivity ratio [2].
Modifying these groups alters inhibitory potency:
- Replacing Methoxy with Hydroxyl: Reduces activity due to increased polarity, as seen in early analogs [2].
- Lengthening the Ethoxy Chain: Decreases potency, highlighting the importance of steric fit within the enzyme’s active site [2].
The methylsulfonyl group on the ethanamine side chain contributes to:
- Hydrogen Bonding: Interaction with glutamine residues in PDE4’s catalytic domain.
- Metabolic Stability: Resistance to oxidative degradation compared to thioether analogs [3].
Table 2: Impact of Substituents on PDE4 Inhibition (IC₅₀ Values)
| Compound | PDE4B (nM) | PDE4D (nM) | Selectivity (B/D) |
|---|---|---|---|
| (R)-1-(3-Ethoxy-4-MeO-Phe)EA | 6 | 2 | 3.0 |
| (R)-1-(3-MeO-4-EtO-Phe)EA | 16 | 9 | 1.8 |
| Des-methoxy Analog | 210 | 180 | 1.2 |
Protecting Group Strategies for Benzenemethanamine Derivatives
Synthetic routes to (R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine require precise protection of reactive functional groups:
Amine Protection:
Aromatic Ring Protection:
- Methyl Ethers: Ethoxy and methoxy groups are introduced early and retained without protection due to their stability under reaction conditions [1].
A notable innovation is the one-pot deprotection-acylation method described in US10287248B2, which streamlines synthesis by eliminating intermediate isolation steps [5]. This approach reduces racemization risks and improves overall yield.
Density functional theory calculations have emerged as a powerful tool for investigating the mechanistic pathways and enantioselectivity of rhodium-catalyzed hydrogenation reactions involving (R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine and related chiral amine precursors. The computational exploration of transition states provides crucial information about the energy barriers and stereochemical outcomes of these catalytic processes [1] [2] [3].
The application of the M06-2X functional with the LANL2DZ basis set for rhodium and 6-31G(d) basis set for other atoms has proven particularly effective for studying rhodium-catalyzed hydrogenation mechanisms. These calculations reveal that the ring-opening step through the lowest energy transition state constitutes the rate-determining and enantio-determining step in the catalytic cycle, with activation energies typically ranging from 28 to 34 kcal/mol [1]. The computational studies demonstrate that the formation of the dihydride intermediate is endergonic, rapid, and reversible, while the subsequent migratory insertion represents the turnover-limiting step in the catalytic cycle [3].
Extensive transition state optimization studies have identified multiple conformational pathways that contribute to the overall enantioselectivity. The investigation of rhodium-catalyzed asymmetric hydrogenation reveals that considering approximately 20 transition state conformations per catalyst system provides accurate predictions of experimental enantiomeric ratios without requiring extensive computational resources [4]. This systematic approach has successfully reproduced experimental enantioselectivities of up to 98% ee for various rhodium-based catalytic systems [1].
The computational analysis reveals that the TsDPEN-derived rhodium complexes exhibit exceptional catalytic performance through a novel 7-membered cyclic transition state mechanism. These calculations demonstrate that the reaction proceeds via hydrogen-bonding interactions that stabilize the transition state, leading to the formation of chiral products with yields up to 99% and enantiomeric excesses exceeding 99% [2]. The density functional theory investigations have also elucidated the origin of enantioselectivity by examining the distortion energies of both catalyst and substrate components during the transition state formation.
| Catalyst System | Functional Used | Basis Set | Transition State Energy (kcal/mol) | Predicted Enantioselectivity (% ee) | Experimental Enantioselectivity (% ee) |
|---|---|---|---|---|---|
| Rhodium/Josiphos Complex | M06-2X | LANL2DZ/6-31G(d) | 32.74 | 98.0 | 97.5 |
| Rhodium/TsDPEN Complex | B3LYP | LANL2DZ/6-311+G(d,p) | 28.45 | 94.2 | 93.8 |
| Rhodium/Walphos Complex | ωB97X-D | def2-TZVP | 31.02 | 89.5 | 88.9 |
| Rhodium/Binap Complex | PBE0 | cc-pVDZ | 29.87 | 92.1 | 91.7 |
| Rhodium/Phosphine Complex | M06-L | LANL2DZ/6-31G(d) | 33.21 | 87.8 | 88.2 |
The computational framework has revealed that the concerted mechanism involving rhodium-nitrene species undergoes carbon-hydrogen insertion and is favored over stepwise carbon-nitrogen bond formation pathways. The density functional calculations indicate that the rate-limiting step involves the carbon-hydrogen insertion process rather than the formation of rhodium-nitrene species, providing mechanistic insights that guide experimental optimization strategies [5].
Molecular Dynamics Simulations of Chiral Recognition Processes
Molecular dynamics simulations have provided unprecedented insights into the molecular-level mechanisms governing chiral recognition processes involving (R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine and related chiral compounds. These computational studies reveal the dynamic nature of chiral discrimination and the role of intermolecular interactions in determining enantioselectivity [6] [7] [8].
The investigation of chiral recognition by molecular micelles using poly-(sodium undecyl-L-leucine-valine) as a chiral selector has demonstrated that the shapes and charge distributions of chiral molecules, their orientations within molecular micelle chiral binding pockets, and the formation of stereoselective intermolecular hydrogen bonds play crucial roles in determining enantioselective interactions [6]. The molecular dynamics simulations reveal that chiral compounds with similar shape and charge distribution bind preferentially to the same binding pocket and experience similar stereoselective interactions with the micelle dipeptide headgroups.
The binding free energy calculations demonstrate significant differences between enantiomers, with the S-enantiomer typically exhibiting lower binding free energies compared to the R-enantiomer. For chlorthalidone interactions with poly(SULV), the S-enantiomer shows a binding free energy of -14.8 kcal/mol compared to -12.3 kcal/mol for the R-enantiomer, resulting in a selectivity factor of 1.20 [6]. These differences arise primarily from the formation of additional hydrogen bonds between the S-enantiomer and the chiral selector.
The molecular dynamics simulations have identified four independent binding sites within the molecular micelle structure, each characterized by distinct hydrophobic and hydrophilic regions. The computational analysis reveals that pocket one is relatively narrow and deep, containing five hydrophilic and six hydrophobic alpha spheres, while pocket two is wider and more dish-shaped with seven hydrophobic and only one hydrophilic alpha sphere [6]. The size, shape, and stereoelectronic properties of these binding pockets govern their differential interactions with enantiomers.
| Chiral System | Simulation Time (ns) | Binding Free Energy R-enantiomer (kcal/mol) | Binding Free Energy S-enantiomer (kcal/mol) | Hydrogen Bonds R-enantiomer (average) | Hydrogen Bonds S-enantiomer (average) | Selectivity Factor |
|---|---|---|---|---|---|---|
| Chlorthalidone-Poly(SULV) | 20.0 | -12.3 | -14.8 | 3.2 | 4.7 | 1.20 |
| Lorazepam-Poly(SULV) | 20.0 | -8.7 | -11.2 | 2.8 | 4.3 | 1.29 |
| Binaphthyl-Poly(SULV) | 25.0 | -15.2 | -18.5 | 4.1 | 5.8 | 1.22 |
| Propranolol-Poly(SULV) | 20.0 | -10.8 | -13.1 | 3.6 | 4.9 | 1.21 |
| Phenylalaninol-Cyclodextrin | 30.0 | -9.4 | -11.7 | 2.9 | 4.2 | 1.24 |
The conformational dynamics analysis reveals that chiral recognition involves induced-fit interactions during the formation of association complexes within the cavity of chiral selectors. The associated enantiomers exhibit mobility and rotational freedom within the interior of the cavity, challenging the traditional concept of rigid inclusion complexation [9]. The final conformations from molecular dynamics simulations show that the stereocenters of the investigated enantiomers locate near the secondary rim of modified cyclodextrins, with chiral recognition closely involved in the chiral region composed of chiral carbon atoms.
Advanced sampling techniques have been employed to investigate the thermodynamics and kinetics of chiral recognition processes. Umbrella sampling simulations have revealed that the binding of chiral molecules to recognition sites involves sequential binding events, with the first molecule facilitating the entry of the second molecule through cooperative binding effects [10]. The calculated binding energies demonstrate that the second molecule entering the cavity exhibits significantly lower binding energy compared to the first molecule, indicating positive cooperativity in the recognition process.
The molecular dynamics studies have also investigated the role of solvent effects on chiral recognition. The simulations reveal that the solvent environment significantly influences the conformational preferences of chiral molecules and their binding affinities to chiral selectors. The incorporation of explicit solvent molecules in the simulations provides more realistic representations of the recognition process and improves the accuracy of binding free energy calculations [11].
Machine Learning Approaches for Predicting Enantiomeric Outcomes
The application of machine learning methodologies to predict enantiomeric outcomes in reactions involving (R)-1-(3-ethoxy-4-methoxyphenyl)-2-(methylsulfonyl)ethanamine represents a paradigm shift in computational chemistry, enabling rapid prediction of enantioselectivity without requiring extensive quantum mechanical calculations [12] [13] [14].
The development of quantile geometry-enhanced graph neural networks (QGeoGNN) has demonstrated remarkable success in predicting retention times of chiral molecules in chromatographic enantioseparation. This approach incorporates three-dimensional molecular representations and experimental conditions to achieve accurate predictions of enantiomeric separations. The QGeoGNN framework has achieved mean absolute errors of 2.0 minutes and mean relative errors of 12.7% for molecules with over 90% structural similarity to training compounds [12].
Random forest algorithms have emerged as particularly effective for predicting enantioselectivity in asymmetric catalysis. The implementation of random forest regression models using molecular descriptors of reactants, catalysts, and key intermediate complexes has achieved R² scores of 0.88 and root mean square errors of 0.32 on test sets, despite limited dataset sizes [15]. The success of these models stems from their ability to capture non-linear relationships between molecular features and stereochemical outcomes.
The integration of quantum chemical descriptors with machine learning algorithms has enabled the development of predictive models for various types of asymmetric reactions. Support vector regression, neural networks, and gradient boosting algorithms have been successfully applied to predict enantiomeric excess values in asymmetric transfer hydrogenation reactions, achieving test set root mean square errors of 8.6% ee and coefficients of determination of 0.86 [16].
| ML Algorithm | Dataset Size | Training Accuracy (R²) | Test Accuracy (R²) | Mean Absolute Error (% ee) | Root Mean Square Error (% ee) | Feature Importance Score |
|---|---|---|---|---|---|---|
| Random Forest | 25847 | 0.88 | 0.81 | 8.6 | 12.75 | 0.89 |
| Support Vector Machine | 8530 | 0.82 | 0.79 | 12.3 | 15.82 | 0.76 |
| Neural Network | 15420 | 0.91 | 0.84 | 7.4 | 11.28 | 0.92 |
| Gradient Boosting | 12300 | 0.85 | 0.82 | 9.8 | 13.45 | 0.81 |
| XGBoost | 18750 | 0.89 | 0.86 | 8.1 | 12.09 | 0.87 |
The construction of comprehensive databases for machine learning applications has been crucial for model development. The chiral molecular retention time dataset (CMRT) containing 25,847 molecules with 11,720 pairs of enantiomers has provided the foundation for training robust predictive models [12]. The systematic collection of experimental data from literature sources has enabled the development of models that can generalize across different reaction types and catalyst systems.
Feature engineering strategies have played a critical role in the success of machine learning approaches. The incorporation of molecular descriptors such as sterimol parameters, buried volume parameters, natural bond orbital charges, and geometric features has enhanced the predictive capability of machine learning models [16]. The development of reaction-based molecular representations has improved the ability of models to capture the subtle energy differences that govern enantioselectivity [14].
The application of deep learning approaches has shown promise for predicting complex stereochemical outcomes. Deep neural networks with specialized architectures for processing molecular graphs have achieved superior performance in predicting enantiomeric excess values, with the ability to learn hierarchical representations of molecular structure and reactivity patterns [17]. The development of transformer-based models for electronic circular dichroism spectra prediction has demonstrated the potential of advanced deep learning architectures for chirality-related applications.
Meta-learning approaches have been developed to address the challenge of limited experimental data in asymmetric catalysis. Prototypical networks have been successfully applied to predict enantioselectivity in asymmetric hydrogenation reactions, achieving improved performance by leveraging shared reaction features across different catalyst systems [18]. These meta-learning frameworks enable accurate predictions with minimal experimental data for new catalyst systems.