Cupric ion
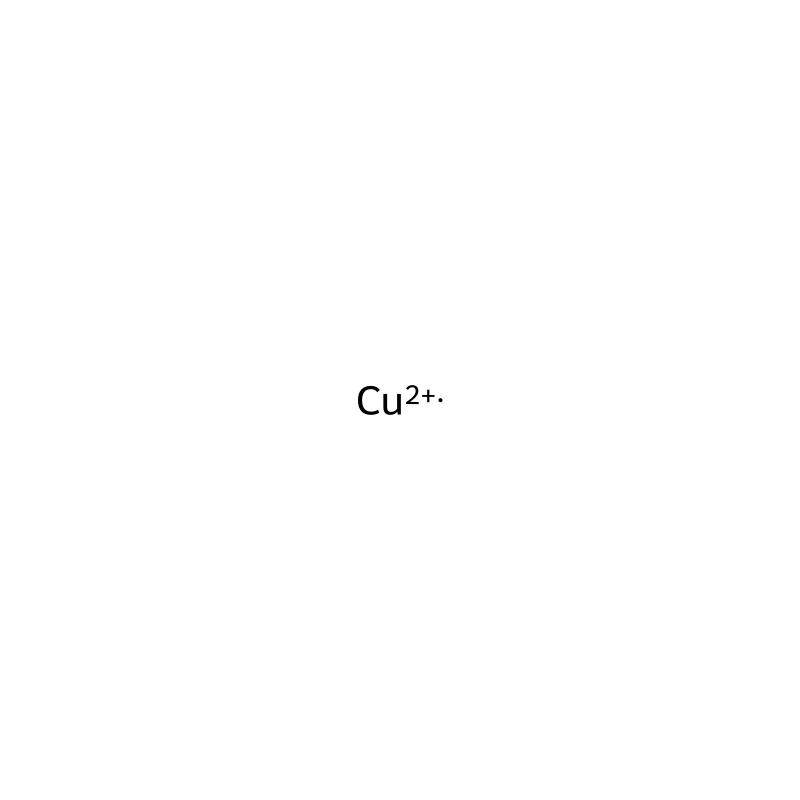
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Canonical SMILES
Copper(2+) is a metabolite found in or produced by Saccharomyces cerevisiae.
See also: Cupric Sulfate (active moiety of); Cupric Chloride (active moiety of); Copper Gluconate (is active moiety of) ... View More ...
The cupric ion, denoted as Cu, is a divalent cation of copper, which is a transition metal with atomic number 29. It plays a crucial role in various chemical processes due to its ability to exist in multiple oxidation states, primarily +1 and +2. The cupric ion is characterized by its blue color in aqueous solutions, resulting from its interaction with water molecules, forming the hexaqua complex . This ion is essential in biological systems and industrial applications due to its catalytic properties and participation in redox reactions.
- Reaction with Acids: When copper metal reacts with concentrated sulfuric acid, it forms cupric ions along with hydrogen gas:Cu(s)+2H_2SO_4(aq)\rightarrow Cu^{2+}(aq)+SO_4^{2-}(aq)+H_2(g)+SO_2(g)+2H_2O(l)$$[2].
- Formation of Complexes: Cupric ions can form complexes with ammonia and hydroxide ions. For example, when mixed with ammonia, the following reaction occurs:[Cu(H_2O)_6]^{2+}(aq)+2NH_3(aq)\rightarrow [Cu(NH_3)_4]^{2+}(aq)+6H_2O(l)$$[2].
- Precipitation Reactions: Cupric ions react with carbonate ions to form copper(II) carbonate:[Cu(H_2O)_6]^{2+}(aq)+CO_3^{2-}(aq)\rightarrow CuCO_3(s)+6H_2O(l)$$[2].
The synthesis of cupric ions can be achieved through several methods:
- Dissolution of Copper Salts: Cupric ions can be obtained by dissolving copper(II) sulfate or copper(II) chloride in water.
- Electrochemical Methods: Electrochemical reduction of copper(II) salts can produce cupric ions in controlled environments.
- Chemical Reduction: Copper(II) oxide can be reduced using reducing agents like hydrogen or carbon monoxide to yield cupric ions .
Cupric ions have diverse applications across various fields:
- Catalysts: They are used as catalysts in organic synthesis and industrial processes.
- Antimicrobial Agents: Due to their ability to disrupt microbial cell membranes, cupric ions are utilized in antimicrobial coatings and treatments .
- Agriculture: They play a role in fertilizers and fungicides due to their essentiality for plant growth.
Research indicates that cupric ions interact with various biological molecules, influencing their behavior. For instance, studies show that cupric ions can enhance the efficacy of certain antibiotics while potentially reducing the effectiveness of others . Furthermore, they have been studied for their role in modulating immune responses and their potential therapeutic applications against cancer due to their ability to induce oxidative stress in tumor cells .
Several compounds exhibit similarities to cupric ions based on their chemical properties and biological activities:
| Compound Name | Chemical Formula | Oxidation State | Unique Characteristics |
|---|---|---|---|
| Cuprous ion | Cu^{+} | +1 | Less stable than cupric; often oxidized to cupric. |
| Silver ion | Ag^{+} | +1 | Similar antimicrobial properties but less versatile. |
| Nickel ion | Ni^{2+} | +2 | Commonly used in batteries; less toxic than cupric. |
| Zinc ion | Zn^{2+} | +2 | Essential trace element; participates in enzyme function. |
| Manganese ion | Mn^{2+}, Mn^{7+} | +2, +7 | Versatile oxidation states; used as catalysts. |
Cupric ions are unique due to their strong redox potential and ability to form stable complexes with various ligands, making them crucial for both biological processes and industrial applications. Their role as both a nutrient and a potential toxin underscores the importance of maintaining balanced levels within biological systems.
The cupric ion, with its d9 electronic configuration, exhibits one of the most pronounced examples of Jahn-Teller distortion among transition metal complexes [1] [2]. The electronic configuration of Cu2+ is [Ar]3d9, which in an octahedral ligand field becomes t2g6eg3 [2]. This configuration places three electrons in the doubly degenerate eg orbitals (dx2-y2 and dz2), resulting in an electronically degenerate ground state that is subject to Jahn-Teller stabilization [1] [3].
The Jahn-Teller theorem predicts that any non-linear molecule in an electronically degenerate state will undergo distortion to remove the degeneracy and lower the overall energy [3] [2]. For cupric ion complexes, this distortion typically manifests as a tetragonal elongation along one axis of the octahedron, creating a (4+2) coordination environment with four shorter equatorial bonds and two longer axial bonds [3] [4] [5].
Structural Characteristics of Jahn-Teller Distortion
Extended X-ray Absorption Fine Structure (EXAFS) studies have provided detailed structural parameters for Jahn-Teller distorted cupric complexes [3] [4] [5]. In aqueous solution, the hexaaquacopper(II) ion exhibits mean equatorial Cu-O bond distances of 1.95-1.96 Å and axial Cu-O bond distances ranging from 2.14 to 2.32 Å [3] [4] [5]. This represents a distortion parameter (difference between axial and equatorial bond lengths) of approximately 0.33-0.37 Å [3].
The magnitude of Jahn-Teller distortion varies significantly depending on the ligand environment [6] [7]. In solid-state compounds such as Cu(H2O)62, the equatorial Cu-O distances are 1.967 Å while the axial distances extend to 2.21 and 2.42 Å [3] [4]. More dramatic distortions are observed in complexes with chelating ligands, where [Cu(en)3]2+ exhibits axial Cu-N bonds of 2.70 Å compared to equatorial bonds of 2.07 Å [8].
Dynamic versus Static Jahn-Teller Effects
Cupric complexes can exhibit either static or dynamic Jahn-Teller distortion depending on the energy barrier between different distorted geometries [2] [9]. Static distortion occurs when the energy difference between the elongated and compressed forms is large compared to thermal energy, resulting in a fixed distorted structure [2]. Dynamic distortion, observed in complexes like K2Pb[Cu(NO2)6], involves rapid interconversion between different distorted forms on a timescale faster than typical spectroscopic measurements [2].
Nuclear magnetic resonance studies have revealed that the inversion time for Jahn-Teller distortion in aqueous cupric solutions is approximately 5.1 × 10-12 seconds [10]. However, recent quantum mechanical/molecular mechanical (QM/MM) molecular dynamics calculations suggest this value may be overestimated by more than an order of magnitude, with actual inversion times closer to 200 femtoseconds [10].
Electronic Origins of Distortion
The driving force for Jahn-Teller distortion in cupric complexes arises from the electronic structure of the d9 configuration [2] [11]. In an ideal octahedral field, the eg orbitals are degenerate, but distortion lifts this degeneracy. Tetragonal elongation lowers the energy of the dz2 orbital while raising the dx2-y2 orbital energy [2]. Since the unpaired electron preferentially occupies the lower-energy dz2 orbital, the overall electronic energy decreases despite the increase in nuclear repulsion energy [2].
Crystal field stabilization energy calculations demonstrate that both z-out (elongation) and z-in (compression) distortions provide equal stabilization energy of -δ1/2, where δ represents the tetragonal splitting parameter [2]. However, z-out distortion predominates due to reduced ligand-ligand repulsion in the elongated geometry [2] [12].
The relationship between electronic structure and distortion is further evidenced by the fact that d9 configuration consistently shows tetragonal elongation across different cupric complexes, from simple aqua complexes to elaborate coordination polymers [13] [7] [14]. This universality underscores the fundamental electronic origin of the Jahn-Teller effect in cupric chemistry.
Ligand Field Stabilization Energies
Ligand Field Stabilization Energy (LFSE) represents a critical parameter for understanding the thermodynamic stability and electronic properties of cupric ion complexes [15] [16] [17]. For the d9 electronic configuration of Cu2+, LFSE calculations provide insights into preferred coordination geometries and the energetic consequences of Jahn-Teller distortion [18] [19].
Theoretical Framework of LFSE Calculations
The calculation of LFSE involves determining the energy difference between the d electron configuration in a ligand field compared to a spherical field reference state [16] [17]. For octahedral complexes, each electron in the t2g orbitals contributes -0.4Δo to the stabilization energy, while electrons in eg orbitals contribute +0.6Δo [16] [17]. The overall LFSE is expressed as:
LFSE = (-0.4 × n(t2g) + 0.6 × n(eg))Δo + mP
where n(t2g) and n(eg) represent the number of electrons in respective orbital sets, Δo is the octahedral crystal field splitting energy, and mP accounts for electron pairing energy [16] [18].
LFSE in Different Coordination Geometries
For the d9 cupric ion in an ideal octahedral field (t2g6eg3), the LFSE equals -0.6Δo [16] [17]. However, Jahn-Teller distortion significantly modifies this value. In a tetragonally elongated octahedral geometry, the d orbital splitting pattern changes, typically resulting in an LFSE of approximately -1.2Δo [2] [17]. This enhanced stabilization energy explains why cupric complexes invariably adopt distorted rather than regular octahedral geometries [1] [19].
Square planar coordination, representing the extreme limit of tetragonal distortion, provides the highest LFSE of approximately -2.4Δo for d9 configuration [17]. This substantial stabilization accounts for the prevalence of square planar geometry in cupric complexes with strong-field ligands such as cyanide or certain nitrogen donors [1] [19].
Tetrahedral coordination yields a significantly lower LFSE of approximately -0.53Δt (where Δt ≈ 4/9Δo), making this geometry less favorable for cupric ions despite reduced ligand-ligand repulsion [18] [17]. The relationship Δt = (4/9)Δo means that tetrahedral LFSE for d9 configuration is approximately -0.24Δo, substantially less than octahedral or square planar alternatives [18].
Factors Influencing LFSE Magnitude
The magnitude of LFSE in cupric complexes depends critically on the ligand field strength, as quantified by the spectrochemical series [18] [20]. Strong-field ligands such as CN-, CO, and en (ethylenediamine) produce large Δo values, resulting in substantial LFSE and favoring low-spin configurations [18]. Weak-field ligands like I-, Br-, and H2O generate smaller splitting energies and correspondingly lower LFSE values [18] [20].
The oxidation state of the metal center also influences LFSE calculations [20]. Higher oxidation states increase the effective nuclear charge, enhancing metal-ligand orbital overlap and increasing ligand field splitting [20]. This relationship explains why Cu3+ complexes, when stabilized, exhibit even greater preference for square planar geometry than Cu2+ analogs [21].
Correlation with Experimental Observables
LFSE calculations correlate well with experimental thermodynamic parameters such as hydration energies and formation constants [19] [17]. The double-humped pattern observed in hydration energies across the first transition series, with minima at d0, d5, and d10 configurations, directly reflects LFSE contributions [17]. Cupric ion, with its moderate LFSE of -0.6Δo in octahedral coordination, falls on the descending portion of this trend [17].
Kinetic properties also reflect LFSE considerations [19] [22]. Cupric complexes exhibit exceptionally fast ligand exchange rates (k ≈ 4.4 × 109 s-1 for water exchange) compared to other divalent first-row transition metals [23] [10] [22]. This lability arises from the reduced LFSE penalty associated with forming five-coordinate intermediates during ligand substitution, as the d9 configuration maintains significant stabilization even in reduced coordination environments [22].
Temperature Dependence and Dynamic Effects
LFSE contributions show temperature dependence through thermal population of higher electronic states and vibrational coupling [24] [25]. In cupric complexes, temperature-dependent coordination number changes have been observed, with higher temperatures favoring geometries with reduced LFSE but greater entropy contributions [24] [25]. This balance between enthalpic (LFSE) and entropic terms determines the predominant coordination geometry under specific conditions [24].
The dynamic nature of cupric coordination, exemplified by rapid water exchange and Jahn-Teller inversion, reflects the relatively small energy differences between alternative coordination modes [10] [26]. LFSE calculations predict these small energy barriers, consistent with the observed fluxional behavior of cupric complexes in solution [24] [10].
Solvation Effects and Hydration Sphere Dynamics
The solvation behavior of cupric ion in aqueous media represents one of the most extensively studied yet debated topics in coordination chemistry [3] [27] [28]. The combination of d9 electronic configuration, Jahn-Teller distortion, and strong electrostatic interactions creates a complex solvation environment characterized by dynamic coordination number changes and rapid ligand exchange [5] [10] [29].
Primary Hydration Shell Structure
High-resolution X-ray Absorption Spectroscopy (XAS) and Extended X-ray Absorption Fine Structure (EXAFS) studies have established that the cupric ion in aqueous solution predominantly adopts a five-coordinate square pyramidal geometry rather than the six-coordinate octahedral structure initially proposed [28] [30]. Frank et al. demonstrated through MXAN (Multiple-scattering X-ray Absorption Near-edge) analysis that [Cu(H2O)5]2+ dominates the solution structure, with the core square pyramidal arrangement exhibiting Cu-O bond distances of approximately 1.96 Å for the four equatorial water molecules [28] [30].
The axial position in the square pyramidal structure shows remarkable dynamic behavior [28] [30]. MXAN analysis revealed that approximately half the time in liquid solution, [Cu(H2O)5]2+ associates with an axially non-bonding water molecule at 2.9 Å [28]. This distant water molecule apparently organizes the second hydration shell and may facilitate the rapid water exchange mechanism observed experimentally [28] [30].
Neutron scattering studies combined with isotopic substitution (H/D) have provided complementary evidence for a mixed coordination environment [31] [32]. Bowron et al. reported average coordination numbers of 4.1 ± 0.3 and 4.5 ± 0.6 water molecules for 0.5 M and 2.0 M cupric perchlorate solutions, respectively [31] [32]. The distribution analysis showed that four-coordinate species predominate in dilute solutions, while five-coordinate forms become more prevalent at higher concentrations [31].
Second Hydration Shell Organization
The second hydration shell of cupric ion exhibits distinct structural features that reflect the influence of the Jahn-Teller distorted primary coordination sphere [5] [33]. LAXS (Large Angle X-ray Scattering) studies reveal a well-defined second shell containing approximately eight water molecules at a mean Cu···O distance of 4.17 Å [3] [4]. This structured second shell contrasts with the more diffuse solvation observed for many other divalent metal ions [5].
The organization of the second hydration shell shows sensitivity to the axial coordination state of the primary shell [28] [30]. When the distant 2.9 Å axial water molecule is present, a complete second shell forms with characteristic Cu···O separations of 3.6-3.8 Å [28]. In the absence of this organizing water molecule, the second shell becomes undetectable to structural probes, indicating significant disorder [28] [30].
Dielectric relaxation spectroscopy studies have provided insights into the effective hydration numbers of cupric ion [34] [35]. These measurements indicate that both Cu2+ and associated anions influence water molecules beyond the first coordination sphere, with effective hydration numbers substantially higher than the primary coordination number [34] [35].
Water Exchange Dynamics and Mechanisms
The cupric ion exhibits the fastest water exchange kinetics among divalent first-row transition metal ions, with rate constants of (4.4 ± 0.1) × 109 s-1 at 298 K determined by 17O nuclear magnetic resonance spectroscopy [23] [10]. Incoherent quasielastic neutron scattering (IQUENS) experiments suggest even faster exchange rates approaching 1010 s-1 [10].
The rapid exchange kinetics arise from the dynamic Jahn-Teller effect, which creates labile axial positions in the coordination sphere [10] [26]. QM/MM molecular dynamics simulations have revealed that water exchange occurs preferentially at the elongated axial positions, with all water molecules changing positions multiple times before an actual exchange event takes place [10].
The water exchange mechanism appears to follow an interchange pathway (I) rather than purely dissociative or associative mechanisms [36] [37]. Variable temperature and pressure studies on related five-coordinate cupric complexes provide activation parameters consistent with an interchange mechanism: ΔH‡ values of 25-43 kJ/mol and ΔV‡ values of -3 to -5 cm3/mol [36] [37].
Solvent Effects and Coordination Number Variation
The coordination behavior of cupric ion shows remarkable sensitivity to solvent properties and concentration effects [38] [39]. Density functional theory calculations using continuum solvation models predict that four-coordinate structures dominate in the gas phase, while five-coordinate geometries become favored in aqueous solution [27] [40] [38].
The small energetic difference (approximately 1.4 kcal/mol) between five- and six-coordinate models suggests that both forms may coexist in solution [27] [40]. Temperature-dependent studies indicate that the dominant coordination number can vary with thermal conditions, reflecting the delicate balance between enthalpic and entropic contributions [24] [25].
In mixed-ligand environments, the hydration sphere dynamics become even more complex [10] [41]. The presence of coordinating anions or nitrogen-donor ligands dramatically accelerates water exchange rates, with mean residence times decreasing from approximately 230 ps in pure water to 35 ps in the presence of ammonia ligands [10]. This enhanced lability reflects the trans effect of heteroligands on the water molecules in axial positions [10].
Temperature and Pressure Dependencies
The hydration sphere structure and dynamics show significant temperature dependence [24] [25] [42]. Freezing aqueous cupric solutions produces characteristic changes in XAS spectra, including the appearance of a shoulder at 8989.6 eV on the rising edge and altered EXAFS patterns [28]. However, the core square pyramidal [Cu(H2O)5]2+ structure persists in frozen solution, although with modified second shell organization [28].
Pressure effects on water exchange kinetics have been studied for model five-coordinate cupric complexes [36] [37]. The negative activation volumes (ΔV‡ = -3 to -5 cm3/mol) support an interchange mechanism involving partial bond formation with incoming water molecules before complete dissociation of departing ligands [36] [37].
Physical Description
Exact Mass
Monoisotopic Mass
Heavy Atom Count
Melting Point
UNII
Other CAS
7440-50-8








