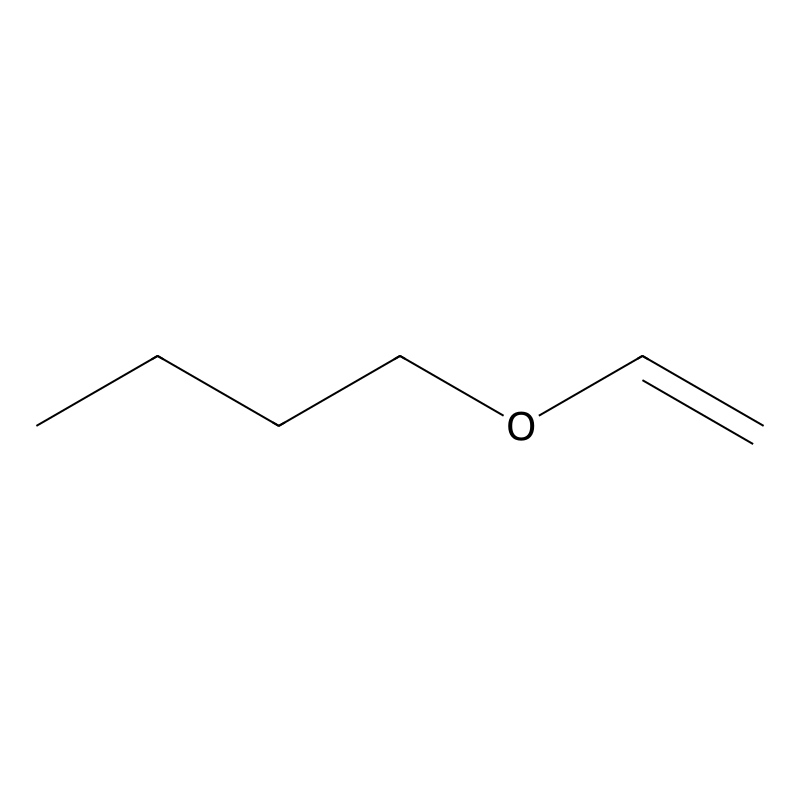
Butyl vinyl ether

Synthesis of Pharmaceutical Compounds:

• Anticancer Drugs: Butyl vinyl ether serves as a valuable building block in the synthesis of specific anticancer agents. Its unique reactivity allows for the creation of complex molecules with potential therapeutic benefits [].
• PDE5 Inhibitors: Research explores the use of butyl vinyl ether in the synthesis of potent inhibitors for phosphodiesterase type 5 (PDE5) enzymes. These inhibitors hold promise for treating various conditions like erectile dysfunction and pulmonary arterial hypertension [].

Polymer Chemistry:

• Copolymer Formation: Butyl vinyl ether readily participates in copolymerization reactions with other monomers, leading to the formation of novel copolymers with diverse properties. These copolymers hold potential applications in various fields, including drug delivery and material science [].
• Comonomer in Resins: Butyl vinyl ether acts as a comonomer in the production of acrylic/vinyl acetate resins. These resins find use in diverse applications, such as paints, coatings, and adhesives [].

Other Research Applications:

Beyond the specific examples mentioned above, butyl vinyl ether's unique chemical properties are explored in various other research areas. These include:

• Organic synthesis: As a versatile reagent, butyl vinyl ether participates in various organic reactions, enabling the creation of complex molecules for diverse research purposes [].
• Material science: Research explores the potential of incorporating butyl vinyl ether into novel materials with specific properties, such as improved strength or conductivity [].

N-Butyl vinyl ether, also known as butyl vinyl ether or butoxyethene, is a highly reactive monomer with the chemical formula $C_6H_{12}O$. It appears as a colorless, transparent liquid that is extremely flammable and irritating to the eyes and respiratory system. Its solubility in water is limited, around 0.10% by weight at 20 °C, but it is miscible with various organic solvents such as benzene and diethyl ether . The compound features a carbon-carbon double bond that is chemically active due to the influence of an alkoxy group, allowing it to undergo various addition reactions to form derivatives .

N-Butyl vinyl ether does not undergo homogeneous polymerization on its own but can be polymerized in the presence of catalysts like aluminum trichloride or boron trifluoride. Under acidic conditions, it hydrolyzes to produce n-butanol and acetaldehyde . The compound can also react with hydroxyl radicals in the vapor phase, with a measured rate constant of $4.3\times 10^{-11}\,\text{cm}^3/\text{s}$ for such reactions .

The primary method for synthesizing n-butyl vinyl ether involves the vinylation of n-butanol with acetylene in the presence of catalysts. A notable superbase catalyst system comprising cesium fluoride, sodium hydroxide, and dimethyl sulfoxide has been developed for this reaction, achieving a conversion rate of 99% for n-butanol with a selectivity of 79% towards isobutyl vinyl ether when conducted at 100 °C under atmospheric pressure .

N-Butyl vinyl ether serves multiple roles in industrial applications:

• Polymer Production: It acts as a monomer for homopolymerization and copolymerization to create polyvinyl ethers, which are utilized in coatings, adhesives, and plasticizers.
• Modifier: The homopolymer of n-butyl vinyl ether is used to enhance properties such as aging resistance and gloss retention in synthetic resin materials.
• Reactive Diluent: It functions as a reactive diluent in ultraviolet curing processes .

N-Butyl vinyl ether shares similarities with several other compounds in terms of structure and reactivity. Here are some comparable compounds:

Uniqueness of N-Butyl Vinyl Ether

N-Butyl vinyl ether stands out due to its high reactivity and versatility as a monomer in polymer chemistry. Its ability to form stable polymers while also being useful in copolymerization processes makes it particularly valuable in industrial applications. Additionally, its specific interactions under acidic conditions differentiate it from similar compounds like ethyl or methyl vinyl ethers.

Impacts of Mixed Gaseous and Particulate Pollutants on Secondary Particle Formation during Ozonolysis of Butyl Vinyl Ether

Peng Zhang, Tianzeng Chen, Jun Liu, Biwu Chu, Qingxin Ma, Jinzhu Ma, Hong He
PMID: 32108486   DOI: 10.1021/acs.est.9b07650

Abstract

To clarify how coexisting atmospheric pollutants affect secondary organic aerosol (SOA) formation, we investigated the effects of mixed gaseous pollutants (CO and SO
) and mixed organic-inorganic (MOI) particles on SOA formation during
-butyl vinyl ether (BVE) ozonolysis. Higher CO levels (90 ppm) were found to significantly change the chemical composition of SOA (prompting monomers while reducing oligomer formation) without causing much change in the overall SOA mass. Based on the positive matrix factorization (PMF) analysis, heterogeneous chemical conversions between preformed and newly formed SOA were the major pathways of SOA formation in the presence of MOI particles. Furthermore, MOI particles had an enhancing effect on SOA formation at 1% relative humidity (RH) but a negligible effect at higher RH (10 and 55%). The enhancing effect was attributed to the formation of multifunctional products resulting from high functionalization of preformed and newly formed SOA. The negligible effect observed was ascribed to the cleavage of unstable oligomers as a result of the reversible oligomerization of preformed and newly formed SOA. Even so, MOI particles could still affect the composition of newly formed SOA. These results highlight the need to account for the significant effect of mixed gaseous and particulate pollutants on both SOA constituents and their evolution.

Chemiluminescence-Induced Free Radical-Promoted Cationic Polymerization

Junzhe Zhu, Ye Zhu, Zhiquan Li, Zihang Yu, Xin Guan, Ren Liu, Yusuf Yagci
PMID: 32100902   DOI: 10.1002/marc.202000004

Abstract

Chemiluminescence (CL) has recently been featured as a new external light source for various photoinduced reactions with attractive features such as eliminating continuous energy supply and advanced light source setups. In the present study, the free-radical-promoted cationic polymerization of cyclohexene oxide, n-butyl vinyl ether, and N-vinyl carbazole under CL irradiation is described. The method is based on the visible-light-induced generation of electron donor radicals from bis-(4-methoxybenzoyl)diethyl germane (BAG), bis(2,4,6-trimethylbenzoyl) phenyl phosphinate, and camphorquinone by CL illumination followed by electron transfer to diphenyl iodonium hexafluorophosphate (Ph
I
PF
) to form corresponding cations capable of initiating cationic polymerization. The applicability of the process to network formation is also demonstrated by using a bifunctional monomer, tri(ethylene glycol) divinyl ether.

Impacts of SO

Peng Zhang, Tianzeng Chen, Jun Liu, Changgeng Liu, Jinzhu Ma, Qingxin Ma, Biwu Chu, Hong He
PMID: 31298843   DOI: 10.1021/acs.est.9b02702

Abstract

Alkyl vinyl ethers are widely used as fuel additives. Despite this, their atmospheric chemistry and secondary organic aerosol (SOA) formation potentials are still not well-known under complex pollution conditions. In this work, we examined the impact of SO
, relative humidity (RH), and particle acidity on the formation and oxidation state (OSc) of SOA from butyl vinyl ether (BVE) ozonolysis. Increasing SO
concentration produced a notable promotion of SOA formation and OSc due to the significant increase in H
SO
particles and formation of more highly oxidized components. Increased RH in the presence of SO
appeared to promote, suppress, and dominate the formation and OSc of SOA in the dry range (1-10%), low RH range (10-42%), and moderate RH range (42-64%), respectively. This highlights the importance of competition between H
O and SO
in reacting with the stabilized Criegee intermediate in BVE ozonolysis at ambient RH. Increased particle acidity mainly contributed to the change in chemical composition of BVE-dominated SOA but not to SOA formation. The results presented here extend previous analysis of BVE-derived SOA and further aid our understanding of SOA formation potential of BVE ozonolysis under highly complex pollution conditions.

Magnetism and spin dynamics of novel encapsulated iron oxide superparamagnetic nanoparticles

Paolo Arosio, Giovanni Baldi, Federica Chiellini, Maurizio Corti, Alberto Dessy, Pietro Galinetto, Matteo Gazzarri, Marco Simone Grandi, Claudia Innocenti, Alessandro Lascialfari, Giada Lorenzi, Francesco Orsini, Anna Maria Piras, Costanza Ravagli, Claudio Sangregorio
PMID: 23736525   DOI: 10.1039/c3dt32805h

Abstract

Encapsulated Fe3O4 nanoparticles of average diameters d = 12 nm are obtained by coprecipitation, in the presence of 2-methoxyethanol hemiester of poly(maleic anhydride-alt-butyl vinyl ether) 5% grafted with poly(ethylene glycol) (VP-MAG nanoparticles). A complete characterization of nude and encapsulated nanoparticles through structural techniques (namely XRD, TEM, SEM), Raman spectroscopy and magnetic measurements has been performed. These nanoparticles compared with commercial compounds (ENDOREM®) present superparamagnetic behavior and nuclear relaxivities that make them promising as magnetic resonance imaging (MRI) contrast agents (CAs). We found that our nanostructures exhibit r2 relaxivity higher than those of commercial CAs over the whole frequency range. The MRI efficiency of our samples was related to their microstructural and magnetic properties.

Mechanistic and kinetic study on the ozonolysis of n-butyl vinyl ether, i-butyl vinyl ether and t-butyl vinyl ether

Dandan Han, Haijie Cao, Yanhui Sun, Ruilian Sun, Maoxia He
PMID: 22534197   DOI: 10.1016/j.chemosphere.2012.03.078

Abstract

Density functional theory (DFT) and ab initio method are employed to elucidate the mechanisms for O(3)-initiated oxidation of n-butyl vinyl ether (n-BVE) and its isomers (i-BVE and t-BVE). For each BVE, the reactions proceed via O(3) cycloaddition resulting in the formation of primary ozonides (POZs) and then two self-decomposition pathways of POZs are followed. Major products are identified to be formaldehyde and butyl formates (CH(3)CH(2)CH(2)CH(2)OCHO for n-BVE, (CH(3))(2)CHCH(2)OCHO for i-BVE and (CH(3))(3)COCHO for t-BVE). The total and individual rate constants for main product channels have been calculated using the modified multichannel Rice-Ramsperger-Kassel-Marcus (RRKM) approach. At 298 K and 101 kPa, the calculated total rate constants are 2.50×10(-16), 3.41×10(-16) and 4.17×10(-16) cm(3) molecule(-1) s(-1) for n-BVE+O(3), i-BVE+O(3) and t-BVE+O(3), respectively, which are in perfect agreement with experimental results. The total rate coefficients are almost pressure independent in the range of 0.001-101 kPa but obviously positive temperature dependent over the whole study temperature range (200-400 K). Also, the favorable reaction pathways have been determined through the estimation of branching ratios. Moreover, the influence of alkoxy group structure on the reactivity of vinyl ethers was examined.

Hemoglobin loaded polymeric nanoparticles: preparation and characterizations

Alberto Dessy, Anna M Piras, Giorgio Schirò, Matteo Levantino, Antonio Cupane, Federica Chiellini
PMID: 21443949   DOI: 10.1016/j.ejps.2011.03.010

Abstract

In the present work polymeric nanoparticles based on Poly (maleic anhydride-alt-butyl vinyl ether) 5% grafted with m-PEG (2000) and 95% grafted with 2-methoxyethanol (VAM41-PEG) were loaded with human hemoglobin (Hb) and characterized from a physicochemical point of view. The assessment of structural and functional features of the loaded Hb was performed and the effect of the introduction of different reducing agents as aimed at minimizing Hb oxidation during the nanoparticles formulation process, was also investigated. Nanoparticles possessing an average diameter of 138±10 nm and physicochemical features suitable for this kind of application were successfully obtained. Although the oxidation of the protein was not avoided during its loading into nanoparticles, the presence of acidic moieties in the polymeric structure is proposed to be directly involved in the protein inactivation mechanism.

Bioactive polymeric materials for targeted administration of active agents: synthesis and evaluation

Federica Chiellini, Anna Maria Piras, Matteo Gazzarri, Cristina Bartoli, Marcella Ferri, Laura Paolini, Emo Chiellini
PMID: 18273833   DOI: 10.1002/mabi.200700228

Abstract

Bioerodible polymers displaying both stealth and targeting properties for the preparation of nanosystems for targeted and controlled delivery of fibrinolytic drugs to the thrombus were prepared by straightforward synthetic routes and characterized. Poly[(maleic anhydride)-alt-(butylvinyl ether)]s were synthesized in the presence of dodecyl mercaptan as chain transfer agent allowing for the preparation of copolymers with tunable molecular weight. 2-Methoxyethanol hemiesters containing antiopsonizing molecules of poly(ethylene glycol) were prepared and further biofunctionalized with a Fab fragment by a two-step reaction. In vitro biocompatibility investigation of the prepared materials supported their suitability for biomedical applications.

Kinetic study of the gas-phase reactions of OH and NO3 radicals and O3 with selected vinyl ethers

Shouming Zhou, Ian Barnes, Tong Zhu, Iustinian Bejan, Thorsten Benter
PMID: 16759126   DOI: 10.1021/jp061431s

Abstract

Kinetic studies on the gas-phase reactions of OH and NO3 radicals and ozone with ethyl vinyl ether (EVE), propyl vinyl ether (PVE) and butyl vinyl ether (BVE) have been performed in a 405 L borosilicate glass chamber at 298 +/- 3 K in synthetic air using in situ FTIR spectroscopy to monitor the reactants. Using a relative kinetic method rate coefficients (in units of cm3 molecule(-1) s(-1)) of (7.79 +/- 1.71) x 10(-11), (9.73 +/- 1.94) x 10(-11) and (1.13 +/- 0.31) x 10(-10) have been obtained for the reaction of OH with EVE, PVE and BVE, respectively, (1.40 +/- 0.35) x 10(-12), (1.85 +/- 0.53) x 10(-12) and (2.10 +/- 0.54) x 10(-12) for the reaction of NO3 with EVE, PVE and BVE, respectively, and (2.06 +/- 0.42) x 10(-16), (2.34 +/- 0.48) x 10(-16) and (2.59 +/- 0.52) x 10(-16) for the ozonolysis of EVE, PVE and BVE, respectively. Tropospheric lifetimes of EVE, PVE and BVE with respect to the reactions with reactive tropospheric species (OH, NO3 and O3) have been estimated for typical OH and NO3 radical and ozone concentrations.

A novel method for the preparation of retinoic acid-loaded nanoparticles

Cesare Errico, Matteo Gazzarri, Federica Chiellini
PMID: 19564952   DOI: 10.3390/ijms10052336

Abstract

The goal of present work was to investigate the use of bioerodible polymeric nanoparticles as carriers of retinoic acid (RA), which is known to induce differentiation of several cell lines into neurons. A novel method, named "Colloidal-Coating", has been developed for the preparation of nanoparticles based on a copolymer of maleic anhydride and butyl vinyl ether (VAM41) loaded with RA. Nanoparticles with an average diameter size of 70 nm and good morphology were prepared. The activity of the encapsulated RA was evaluated on SK-N-SH human neuroblastoma cells, which are known to undergo inhibition of proliferation and neuronal differentiation upon treatment with RA. The activity of RA was not affected by the encapsulation and purification processes.

Novel chlorhexidine releasing system developed from thermosensitive vinyl ether-based hydrogels

Arlin S Kiremitçi, Arzu Ciftçi, Meral Ozalp, Menemşe Gümüşderelioğlu
PMID: 17471518   DOI: 10.1002/jbm.b.30834

Abstract

The aim of this study is to determine the effective concentrations of chlorhexidine on the release for prolonged periods of time from a novel hydrogel system. A hydrogel that exhibits a volume phase transition in response to temperature was synthesized by radiation copolymerization of ethylene glycol vinyl ether and butyl vinyl ether in the presence of crosslinking agent, diethylene glycol divinyl ether. Hydrogel samples in the disc form (diameter, 10 mm and height, 1.5 mm) were utilized as a matrix for the release of an antimicrobial agent, chlorhexidine diacetate. Chlorhexidine loading into the hydrogel was performed by water sorption at 4 degrees C, which allows high swelling and thus high loading capacity, i.e., approximately 36 mg drug per gram of dry gel. Chlorhexidine release was examined as short-term (24 h) and long-term (27 days) by UV spectrophotometer. Microbial studies were carried out by micro-dilution method in order to determine the effectiveness of the drug release. Minimum inhibitory concentration values for the pathogens of Streptococcus mutans and Lactobacillus casei were determined. The long-term chlorhexidine release is initially very fast. After that, the drug release reaches a slow but a steady rate. Such a release pattern provides an effective drug release. The prolonged release of chlorhexidine is continued up to the 27th day. MIC values for the two pathogens have been shown that the release rate from disc is effective to inhibit the growth of pathogens. These in vitro drug release results suggested that the thermosensitive hydrogel system developed in this study can be evaluated as a delivery system for the release of chlorhexidine.