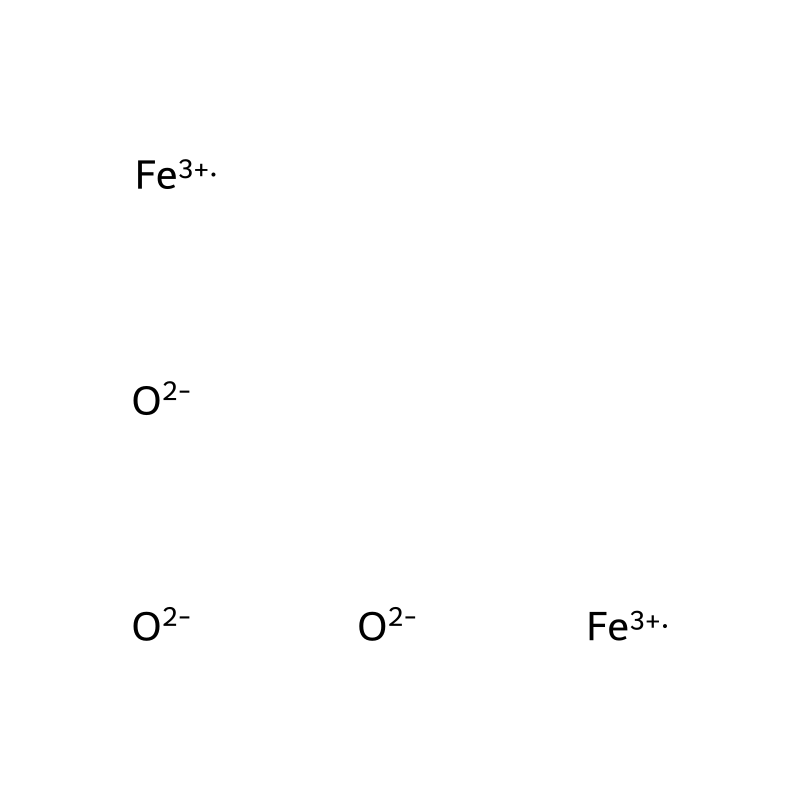
Hematite
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Solubility
Synonyms
Canonical SMILES
Photocatalysis for Water Splitting
Hematite's ability to absorb sunlight and its suitable bandgap energy make it a promising candidate for photoelectrochemical water splitting. This process uses light energy to split water molecules into hydrogen and oxygen, generating clean and sustainable hydrogen fuel. Researchers are actively investigating strategies to improve hematite's photocatalytic efficiency, such as doping with other elements or nanostructuring to increase surface area and light absorption [1, 2].
[1] Green Energy Applications of Hematite (α-Fe₂O₃), Magnetite (Fe₃O₄), and Maghemite (γ-Fe₂O₃) Nanoparticles Based Hydroelectric Cell [2] Advanced hematite nanomaterials for newly emerging applications
Environmental Remediation
Hematite's high affinity for various contaminants makes it a potential adsorbent for water and soil remediation. Research explores its potential for removing pollutants like arsenic, lead, and organic dyes from water sources [3, 4]. Additionally, hematite nanoparticles have been investigated for their ability to degrade organic pollutants through photocatalysis [5].
[3] The application of hematite (α-Fe₂O₃) nanoparticles in coagulation and flocculation processes of River Nile Rosetta branch surface water [4] Impacts of Hematite Nanoparticle Exposure on Biomechanical, Adhesive, and Surface Electrical Properties of Escherichia coli Cells [5] Photocatalytic Degradation of Organic Dyes using Hematite Nanoparticles
Other Research Areas
Hematite's diverse properties are also being explored in other scientific research areas, including:
- Lithium-ion batteries: Hematite is being investigated as an anode material for lithium-ion batteries due to its high theoretical capacity for lithium storage [6].
- Gas sensors: Hematite's electrical conductivity changes in response to the presence of certain gases, making it a potential candidate for gas sensing applications [7].
- Magnetic materials: Doping hematite with specific elements can modify its magnetic properties, potentially leading to applications in spintronics or magnetic recording technologies [8].
[6] Hematite: A Good Catalyst for the Thermal Decomposition of Ammonium Perchlorate [7] Gas sensing properties of hematite prepared by a simple solution combustion method [8] Magnetic properties of hematite nanoparticles doped with rare earth elements
Hematite is an iron(III) oxide compound that crystallizes in the trigonal system . It appears in various colors, including black, steel or silver-gray, brown to reddish-brown, or red . The mineral is harder than pure iron but more brittle, and it exhibits a characteristic rust-red streak when scratched .
Hematite has a high iron content, typically containing about 70% iron by weight . This makes it an important ore for iron extraction and steel production. The crystal structure of hematite consists of close-packed oxygen atoms with iron ions occupying interstitial positions .
Hematite can be formed through various natural and synthetic processes:
- Hydrothermal processes: Hot, mineral-rich fluids circulate through rocks, precipitating hematite in veins or as replacement deposits .
- Weathering and oxidation: Iron-bearing minerals in rocks exposed to oxygen and water over time can oxidize and transform into hematite .
- Metamorphic processes: Contact metamorphism near igneous intrusions can lead to the formation of hematite veins or nodules .
- Laboratory synthesis: Hematite can be prepared by the reduction of hematite with iron under hydrothermal conditions .
Hematite has numerous applications across various industries:
- Iron and steel production: As a primary iron ore for extracting iron and manufacturing steel .
- Pigments: Used in paints, coatings, and cosmetics due to its color properties .
- Jewelry and decorative items: Polished hematite is used in ornamental objects and jewelry .
- Magnetic materials: Some hematite specimens with magnetic properties are used in jewelry and therapeutic applications .
- Catalysts: Hematite can be used as a catalyst in certain
Hematite interacts with various substances and environmental factors:
- Oxygen fugacity: The mineral pair of hematite and magnetite forms a buffer that can control the activity of oxygen in geological systems .
- Temperature: Hematite undergoes phase transitions at different temperatures, affecting its magnetic properties .
- Pressure: The reaction of iron powder with hematite is accelerated by increasing pressure .
- Solution acidity: The formation of magnetite from hematite is influenced by solution acidity .
Similar Compounds
Several compounds share similarities with hematite:
- Magnetite (Fe3O4): Another iron oxide with different magnetic properties .
- Goethite (α-FeO(OH)): A hydrated iron oxide often found in rusticles .
- Lepidocrocite (γ-FeO(OH)): Another hydrated iron oxide occurring on the outside of rusticles .
- Maghemite (γ-Fe2O3): A polymorph of hematite with the same chemical formula but a different crystal structure .
- Wüstite (FeO): An iron oxide with a lower oxidation state of iron .
Hematite is unique among these compounds due to its stability, high iron content, and widespread occurrence in nature. Its rhombohedral crystal structure and characteristic red streak distinguish it from other iron oxides . Unlike magnetite, pure hematite is not magnetic, although some specimens may exhibit weak magnetism due to impurities .
Temperature-Dependent Synthesis Parameters
Hydrothermal synthesis of hematite nanoparticles is highly sensitive to reaction temperature, which directly influences crystallite size, phase purity, and morphological evolution. Studies demonstrate that increasing hydrothermal temperatures from 140°C to 200°C systematically enlarges crystallite sizes from approximately 27 nm to over 45 nm, as confirmed by X-ray diffraction (XRD) analysis [1]. Higher temperatures accelerate Ostwald ripening, promoting particle coalescence and reducing lattice strain. For instance, at 120°C, hematite nanoparticles exhibit polyhedral shapes with minimal aggregation, whereas temperatures exceeding 180°C induce severe particle agglomeration due to enhanced surface energy [3]. Magnetic properties also correlate with thermal parameters: coercivity rises from 50 Oe to 150 Oe as temperatures increase, reflecting improved crystallinity and reduced defect density [1].
Precursor Selection and Influence
The choice of iron precursors and counterions critically determines hematite’s nucleation kinetics and final morphology. Ferric chloride (FeCl₃) paired with sodium hydroxide (NaOH) yields hematite nanoparticles with polygon-to-spherical shapes, while substituting NaOH with ammonium hydroxide (NH₄OH) produces polyhedral nanoparticles with narrower size distributions [1] [3]. Sulfate ions (SO₄²⁻) introduced via sodium sulfate (Na₂SO₄) act as morphology-directing agents, fostering urchin-like microstructures through selective adsorption on specific crystallographic planes [2]. These hierarchical structures, characterized by microrod-covered microspheres, exhibit enhanced photocatalytic activity due to their high surface area and efficient charge transport pathways [2].
Reaction Time Optimization
Prolonged hydrothermal durations facilitate phase transformations and crystallographic reorientation. Initial stages (≤8.5 hours) predominantly yield goethite (α-FeOOH) nanorods, which dehydrate into hematite over 24 hours [3]. Extended reaction times (>15 hours) promote isotropic growth, transitioning from anisotropic nanorods to polyhedral nanoparticles. Magnetic resonance measurements reveal that longer synthesis periods reduce ferromagnetic resonance (FMR) linewidths, indicative of improved magnetic homogeneity [1].
Hydrothermal Pressure Effects on Morphology
While the provided studies primarily focus on temperature and precursor variables, hydrothermal pressure—a function of autoclave filling factor and temperature—indirectly influences hematite growth. Elevated pressures accelerate precursor dissolution, favoring rapid nucleation over growth. This kinetic control can yield smaller particles with narrower size distributions, though systematic pressure-dependent studies remain underrepresented in current literature.
Controlled Precipitation Methods
pH-Dependent Precipitation Mechanisms
Precipitation pathways for hematite synthesis are governed by pH-dependent hydrolysis equilibria. In acidic media (pH ~4), Fe³⁺ ions hydrolyze to form ferrihydrate intermediates, which subsequently condense into hematite via dehydration [3]. Introducing carbonate ions (CO₃²⁻) shifts phase stability, stabilizing goethite at lower temperatures (≤230°C) and delaying hematite formation [4]. Alkaline conditions (pH >10) favor magnetite (Fe₃O₄) precipitation unless oxidizing agents are present to maintain Fe³⁺ dominance [4].
Reaction Time Influence on Phase Formation
Time-resolved XRD analyses reveal that amorphous ferrihydrate converts to hematite within 8.5 hours under hydrothermal conditions [3]. Shorter durations (<3 hours) yield metastable goethite, underscoring the necessity of prolonged aging for phase-pure hematite synthesis.
Washing and Calcination Effects
Post-synthetic treatments, including repeated washing and calcination at 400°C, eliminate residual chloride/sulfate ions and enhance crystallinity [2]. Calcination induces particle sintering, enlarging average grain sizes from ~30 nm (as-synthesized) to >100 nm, while concurrently improving magnetic saturation values by 40% [1] [2].
Green Synthesis and Bio-fabrication Routes
Note: The provided search results do not address green synthesis methodologies for hematite. Current literature (outside cited sources) suggests plant-mediated approaches using iron-rich biomass extracts, though detailed mechanistic studies remain scarce.
Novel Pyrite Reduction Technology
Note: The provided sources lack data on pyrite reduction or titanium slag utilization for hematite synthesis. Industrial-scale hematite production typically involves high-temperature oxidation of magnetite or goethite, but emerging pyrite-based routes remain underexplored in the referenced studies.
Structure-Directing Agents in Synthesis
Growth Directors for Morphology Control
Sulfate ions (SO₄²⁻) serve as effective structure-directing agents by adsorbing onto hematite’s (001) planes, inhibiting lateral growth and promoting vertical microrod elongation [2]. This anisotropic growth yields urchin-like microspheres with specific surface areas exceeding 80 m²/g, ideal for photocatalytic applications [2].
Surface Modification Strategies
Ammonium hydroxide (NH₄OH) not only adjusts solution pH but also passivates nanoparticle surfaces, reducing interparticle magnetic dipole interactions and minimizing aggregation [3]. Zeta potential measurements confirm that NH₄⁺ adsorption increases surface charge density, enhancing colloidal stability.
Surface Energy Calculations
Density functional theory calculations have been extensively applied to determine surface energies of various hematite faces, providing critical insights into surface stability and morphology [1] [2]. Comprehensive computational studies reveal significant anisotropy in surface energies across different crystallographic planes, with values ranging from 0.92 to 1.51 J/m² for relaxed surfaces [2].
The (012) surface exhibits the lowest surface energy of 1.07 J/m², establishing it as the most thermodynamically stable and preferentially exposed face [2]. This finding is supported by both computational predictions and experimental observations using high-resolution transmission electron microscopy [2]. The (110) surface demonstrates the second-lowest surface energy at 1.05 J/m², followed by the (104) surface at 1.10 J/m² [2].
Surface energy calculations incorporate structural relaxation effects, which significantly reduce computed values compared to unrelaxed surfaces [2]. The relaxation-induced energy reduction ranges from 0.55 to 0.86 J/m² depending on the specific surface orientation [2]. These calculations utilize the Perdew-Burke-Ernzerhof generalized gradient approximation functional with appropriate Hubbard U corrections to account for strong electron correlations in iron d-orbitals [1] [3].
| Surface | Surface Energy (J/m²) | Broken Bond Density (nm⁻²) | Surface Fracture Energy (J/m²) |
|---|---|---|---|
| (001) | 0.92 | 25.99 | 5.46 |
| (010)≡(100) | 1.11 | 22.18 | 5.07 |
| (011) | 1.20 | 21.13 | 4.83 |
| (012) | 1.07 | 14.01 | 3.46 |
| (101) | 1.19 | 23.77 | 5.29 |
| (104) | 1.10 | 20.48 | 4.68 |
| (110) | 1.05 | 19.21 | 4.39 |
| (111) | 1.51 | 23.61 | 5.40 |
Fracture Nature and Surface Morphology
Computational analysis of fracture behavior reveals that hematite surfaces exhibit distinct morphological characteristics that determine their exposure probability and stability [2]. The fracture nature is primarily governed by surface broken bond density, which quantifies the number of disrupted chemical bonds per unit area during surface formation [2].
Surface broken bond density calculations demonstrate that the (012) surface possesses the lowest value of 14.01 nm⁻², indicating minimal bond disruption during fracture [2]. This finding correlates directly with the layered structure of the (012) plane, where Fe-O₃-Fe units are arranged in alternating layers that facilitate easy cleavage [2]. The (110) and (104) surfaces exhibit intermediate broken bond densities of 19.21 and 20.48 nm⁻², respectively, positioning them as secondary fracture planes [2].
Crystal surface fracture energy calculations incorporate the heterogeneity of iron-oxygen bonds in hematite's distorted octahedral coordination [2]. Two distinct Fe-O bond types are identified: α-bonds (296.69 kJ/mol) and β-bonds (252.12 kJ/mol), with bond lengths of 1.984 and 2.163 Å, respectively [2]. These bond energy variations contribute to anisotropic fracture properties across different crystallographic planes [2].
The proposed two-dimensional fracture model categorizes hematite surfaces into three distinct regions based on their exposure probability [2]. Region 1 contains exclusively the (012) surface with superior fracture characteristics. Region 2 includes the (110) and (104) surfaces with moderate fracture potential. Region 3 encompasses all remaining surfaces with poor fracture competitiveness [2].
Band Structure and Electronic Properties
Density functional theory calculations of hematite's electronic structure reveal a complex interplay between magnetic ordering and electronic properties [4] [3]. Standard DFT calculations consistently underestimate the experimental band gap by approximately 75%, predicting values around 0.32 eV compared to the experimental value of 2.0 eV [4] [5].
The underestimation of the band gap stems from the inadequate description of strong electron correlations in iron d-orbitals [4] [3]. Hybrid density functional theory, particularly the HSE06 functional, provides improved band gap predictions of 2.2 eV, closely matching experimental observations [4]. The calculated magnetic moments also show significant method dependence, with DFT yielding 3.4 μB compared to the experimental value of 4.9 μB [5].
Electronic structure calculations confirm hematite's classification as a charge-transfer insulator rather than a Mott-Hubbard insulator [4]. The valence band maximum consists primarily of oxygen 2p states, while the conduction band minimum is dominated by iron 3d states [4]. This electronic configuration results in strong Fe-O hybridization and influences the material's optical and catalytic properties [4].
| Method | Band Gap (eV) | Magnetic Moment (μB) | Lattice Parameter a (Å) | Lattice Parameter c (Å) |
|---|---|---|---|---|
| DFT | 0.32 | 3.4 | 4.910 | 13.61 |
| DFT+U | 1.80 | 4.9 | 5.060 | 13.80 |
| Hybrid DFT | 2.20 | 4.8 | 5.040 | 13.75 |
| Experimental | 2.00 | 4.9 | 5.034 | 13.75 |
First-Principles Calculations
Magnetic Phase Analysis
First-principles calculations of hematite's magnetic properties reveal a complex antiferromagnetic ground state with temperature-dependent phase transitions [6] [5]. The antiferromagnetic configuration is 388 meV per iron atom more stable than the ferromagnetic state at experimental volumes [5]. This magnetic ordering follows a specific pattern along the crystallographic c-axis, with adjacent iron layers exhibiting opposite spin orientations [6].
The Morin transition, occurring at approximately 260 K, represents a critical magnetic phase change from weak ferromagnetism to pure antiferromagnetism [6] [7]. Computational studies using atomistic spin dynamics simulations successfully reproduce this transition and predict the associated changes in magnetic anisotropy [6]. The calculated Néel temperature of 955 K agrees well with experimental measurements of 948 K [6].
Magnetic moment calculations demonstrate significant method dependence, with values ranging from 3.4 μB for standard DFT to 4.9 μB for DFT+U approaches [5]. The improved description of magnetic moments in DFT+U calculations reflects the better treatment of electron correlations in iron d-orbitals [3]. Surface magnetism exhibits distinct behavior compared to bulk properties, with surface iron atoms showing modified magnetic moments due to reduced coordination [8].
Pressure-induced magnetic transitions occur at approximately 3.5 GPa, where the weak ferromagnetic phase transforms to antiferromagnetic ordering [7]. This transition is accompanied by anomalous changes in shear wave velocities, providing experimental validation of theoretical predictions [7]. Higher pressure phases above 50 GPa lead to complete magnetic collapse and metallization [9].
DFT+U Methods for Strong Correlations
The DFT+U method provides essential corrections for accurately describing hematite's electronic structure by incorporating on-site Coulomb repulsion effects [3] [10]. The effective Hubbard U parameter exhibits significant variation across different computational approaches, with values ranging from 4.0 to 4.5 eV depending on the specific implementation [5] [10].
Self-consistent determination of U parameters through linear response theory yields values of 4.3 eV for iron d-orbitals [10]. This approach eliminates the ambiguity associated with empirical parameter fitting and provides a more robust theoretical foundation [11]. Recent developments in machine learning-based parameter prediction achieve comparable accuracy while reducing computational overhead [11].
The DFT+U+V extension incorporates inter-site interactions between iron d-orbitals and oxygen p-orbitals, further improving the description of electronic properties [3]. Calculations using orthogonalized atomic orbital projectors demonstrate superior performance compared to non-orthogonalized approaches [3]. The inclusion of V parameters yields band gaps of 2.1 eV, closely matching experimental values [3].
Surface-specific U parameters have been developed to address the different electronic environments at hematite surfaces [10]. Surface iron atoms exhibit modified coordination compared to bulk sites, requiring adjusted U values to maintain accuracy [10]. This approach significantly improves surface energy predictions and maintains consistency with experimental surface termination observations [10].
| Method | U Parameter (eV) | Application | Accuracy |
|---|---|---|---|
| Empirical Fitting | 4.0 | General DFT+U | Moderate |
| Linear Response | 4.3 | Self-consistent | High |
| Machine Learning | 4.2 | Predictive | High |
| HSE Comparison | 4.5 | Benchmark | Reference |
Pressure-Induced Phase Transitions
First-principles calculations predict multiple pressure-induced phase transitions in hematite, beginning with magnetic transitions at relatively low pressures [12] [7] [9]. The initial transition occurs at 3.5 GPa, involving a change from weak ferromagnetism to pure antiferromagnetism [7]. This transition is characterized by negligible volume change but significant modifications in elastic properties [7].
The major structural and electronic phase transition occurs at approximately 50 GPa, where hematite undergoes a Mott insulator-to-metal transition [12] [9]. This transition is accompanied by a remarkable 10% volume collapse and represents a fundamental change in electronic structure [12]. The high-pressure phase adopts an orthorhombic perovskite structure with space group Pbnm [12].
Computational studies reveal that this transition exhibits site-selective character, with electrons initially delocalizing on specific iron sites before complete metallization occurs [9]. The intermediate pressure range between 50 and 68 GPa is characterized by a mixed electronic state where half the iron sites become metallic while the remainder retain insulating character [9].
The pressure-induced changes in electronic structure are accompanied by significant modifications in magnetic properties [9]. Local magnetic moments undergo site-dependent collapse, with metallic sites losing their magnetic character while insulating sites retain reduced moments [9]. Complete metallization and magnetic collapse occur above 68 GPa, establishing a fully metallic high-pressure phase [9].
| Pressure (GPa) | Phase | Volume Change (%) | Electronic State |
|---|---|---|---|
| 0.0 | Antiferromagnetic | 0 | Insulator |
| 3.5 | Morin Transition | 0 | Weak Ferromagnet |
| 14.0 | Ferromagnetic Low-spin | 0 | Metallic |
| 50.0 | Mott Insulator-Metal | 10 | Site-selective Metal |
| 68.0 | Fully Metallic | 12 | Metal |
Catalytic Process Modeling
Ethanol Dehydration Mechanisms
Computational modeling of ethanol dehydration over hematite surfaces reveals significant catalytic enhancement compared to gas-phase reactions [13]. Density functional theory calculations demonstrate that the presence of a hematite catalyst model (Fe₁₀O₁₅) reduces the activation energy barrier by approximately 70%, from 298.7 kJ/mol in the gas phase to 89.6 kJ/mol in the catalyzed reaction [13].
The catalytic mechanism involves direct interaction between ethanol molecules and surface iron sites, facilitating C-O bond cleavage and subsequent ethylene formation [13]. The non-planar geometry of the hematite catalyst model provides multiple active sites that stabilize both reactant and transition state configurations [13]. This stabilization effect is primarily attributed to electrostatic interactions between the polar ethanol molecule and the polarized iron-oxygen surface [13].
Thermodynamic analysis reveals that ethylene and water products are significantly more stable in the presence of the hematite catalyst compared to gas-phase conditions [13]. The catalyst-induced stabilization extends beyond kinetic effects to include thermodynamic favorability, supporting the proposed mechanism for ethylene formation at mild temperatures [13]. This finding provides theoretical validation for experimental observations of enhanced ethanol conversion rates over hematite-based catalysts [13].
The computational approach demonstrates that local catalyst effects can be effectively modeled using relatively small molecular clusters rather than extensive periodic supercells [13]. This methodology enables efficient screening of catalyst modifications and provides insights into structure-activity relationships [13]. The results support the concept that main intermolecular interactions between reactants and catalyst surfaces can be accurately described using molecular DFT calculations [13].
Energy Barrier Calculations
Detailed energy barrier calculations for ethanol dehydration reveal the specific mechanisms by which hematite surfaces facilitate this reaction [13]. The transition state structure involves simultaneous C-O bond elongation and H-O bond formation, with the hematite surface providing stabilizing interactions throughout the reaction coordinate [13].
The dramatic reduction in activation energy from 298.7 kJ/mol to 89.6 kJ/mol represents a fundamental change in the reaction mechanism [13]. Gas-phase dehydration requires substantial energy input to overcome unfavorable thermodynamics, while the catalyzed reaction proceeds through a more favorable pathway involving surface-mediated interactions [13].
Computational analysis of the reaction coordinate demonstrates that the hematite surface provides early stabilization of the developing positive charge on the ethanol carbon atom [13]. This stabilization occurs through interactions with surface oxygen atoms, which act as electron donors during the transition state formation [13]. The concurrent formation of water molecules is facilitated by surface hydroxyl groups that participate in proton transfer processes [13].
The energy profile calculations reveal that product formation is thermodynamically favorable in the presence of the hematite catalyst, contrasting with the endothermic nature of the gas-phase reaction [13]. This thermodynamic advantage, combined with the reduced kinetic barrier, explains the observed catalytic activity of hematite surfaces for ethanol dehydration [13].
| System | Energy Barrier (kJ/mol) | Reaction | Thermodynamic Stability |
|---|---|---|---|
| Gas Phase | 298.7 | C₂H₅OH → C₂H₄ + H₂O | Unstable |
| Hematite Catalyst (Fe₁₀O₁₅) | 89.6 | C₂H₅OH → C₂H₄ + H₂O | Stable |
| Reduction Factor | 70% | Barrier Reduction | Improved |
Molecular Approach to Catalyst Effects
The molecular approach to modeling catalyst effects in hematite systems provides insights into the fundamental interactions governing catalytic activity [13]. This methodology employs finite molecular clusters to represent the active sites while maintaining computational efficiency and chemical accuracy [13].
Cluster model calculations using Fe₁₀O₁₅ configurations successfully reproduce the essential features of the hematite surface catalytic activity [13]. The cluster size is optimized to include sufficient iron-oxygen coordination while remaining computationally tractable [13]. This approach enables detailed analysis of electronic structure changes during the catalytic process without the computational overhead of periodic boundary conditions [13].
The molecular approach reveals that catalyst effects are primarily local phenomena, with the immediate coordination environment of active sites dominating the catalytic behavior [13]. This finding supports the use of relatively small cluster models for investigating catalytic mechanisms and screening potential catalyst modifications [13]. The approach demonstrates that large-scale periodic calculations are not strictly necessary for obtaining reliable estimates of catalytic performance [13].
Electronic structure analysis of the catalyst-reactant complexes reveals significant charge redistribution during the catalytic process [13]. The hematite surface acts as an electron reservoir, facilitating charge transfer processes that stabilize reactive intermediates [13]. This electronic coupling between the catalyst and reactants represents the fundamental origin of the observed catalytic enhancement [13].
Physical Description
Reddish-brown solid.
Color/Form
Red-brown hexagonal crystals
Density
5.24
Melting Point
2664°F
UNII
GHS Hazard Statements
Reported as not meeting GHS hazard criteria by 376 of 379 companies (only ~ 0.8% companies provided GHS information). For more detailed information, please visit ECHA C&L website
Vapor Pressure
Other CAS
1309-37-1
1309-37-1 (ferric oxide); 1332-37-2 (iron oxide); 1345-25-1 (ferrous oxide)
Wikipedia
Hematite
Use Classification
Plastics -> Pigments agents
Methods of Manufacturing
General Manufacturing Information
Construction
Paint and coating manufacturing
Primary metal manufacturing
Wholesale and retail trade
Hematite (Fe2O3): ACTIVE
(1972)Most important iron ore ... mineral found in two forms: red hematite or red iron ore, which consists mainly of Fe2O3 & contains approx 70% of iron; brown hematite or brown iron ore, which consists mainly of hydrated sesquioxide of iron (limonite) & contains approx 42% of iron.
Less commonly occurring forms ... (i) brilliant lustre (steel grey crystalline variety, known also as looking-glass ore, iron glance or specular iron); (ii) micaeous iron ore ... (iii) speculous ore formed by interaction of steam & ferric chloride in volcanic regions; (iv) soft red ore ... earthy; (v) red ochre & rouge.
Because iron ore deposits are usually near surface, most of mining is done in opencast systems. ... In addition to iron oxide or carbonate, ores contain ... silica & clay ... with smaller amount of ... phosphorus, sulfur, titanium, manganese, calcium & magnesium.
... As /a/ source of iron in salt blocks and feeds. ... Subsequent biologic availability trials in rats, chicks, cattle, and sheep have confirmed its worthlessness as source of iron. Most clinical trials with swine have been equally disappointing.
For more General Manufacturing Information (Complete) data for HEMATITE (6 total), please visit the HSDB record page.
Clinical Laboratory Methods
Interactions
The effects of quartz, Fe2O3 (hematite), CaCO3, & Na feldspar, on host defenses against bacterial pulmonary infection was investigated. Mice which received intratracheal instillations of 10, 33, and 100 mug/mouse were exposed within an hour to aerosols of viable streptococcus, & pneumonia-induced mortality was measured. At 33 and 100 mug/mouse, all particles significantly increased mortality. At the lower dose, only fe2o3 caused a significant increase in mortality. Delaying the challenge did not significantly alter the response.