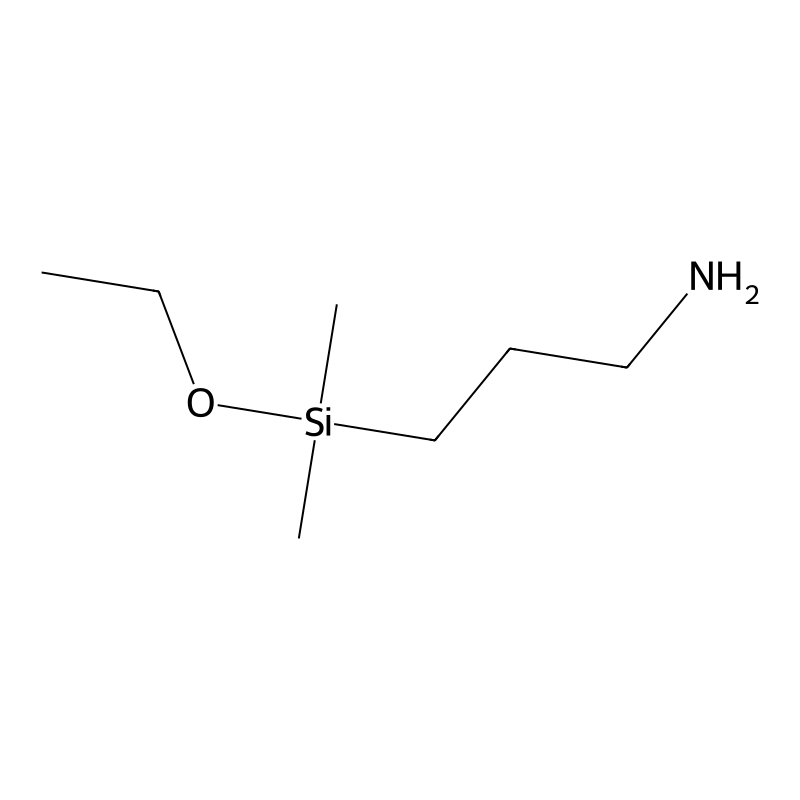
1-Propanamine, 3-(ethoxydimethylsilyl)-

1-Propanamine, 3-(ethoxydimethylsilyl)- (CAS 18306-79-1) is a monofunctional aminosilane used for creating well-defined, amine-terminated surfaces on substrates like glass, silica, and metal oxides. Unlike the more common trifunctional analogs such as (3-Aminopropyl)triethoxysilane (APTES), its single ethoxy group provides a critical point of control over the silanization process. This structural difference is fundamental to its value proposition, as it prevents the uncontrolled, three-dimensional polymerization that often complicates processes using trialkoxysilanes, instead favoring the formation of a true self-assembled monolayer (SAM). This makes it a key material for applications requiring high reproducibility and a well-defined surface architecture, including microelectronics, biosensors, and nanoparticle functionalization.

Direct substitution of monofunctional 1-Propanamine, 3-(ethoxydimethylsilyl)- with trifunctional aminosilanes like (3-Aminopropyl)triethoxysilane (APTES) or (3-Aminopropyl)trimethoxysilane (APTMS) often leads to process failure and poor device performance. The three alkoxy groups on APTES/APTMS can hydrolyze and cross-link uncontrollably in the presence of trace moisture, leading to the formation of thick, rough, and poorly defined polymeric films instead of a uniform monolayer. This tendency for self-condensation complicates solution stability, bath lifetime, and deposition reproducibility. For applications where surface morphology, layer thickness, and binding site density must be precisely controlled, such as in biosensors or high-performance composites, the monofunctional nature of CAS 18306-79-1 is a non-negotiable processing and performance requirement.

Solution Stability

The rate of silane hydrolysis is a critical parameter for process control, directly impacting the stability and working life of treatment solutions. The molecular structure significantly affects this rate, with fewer alkoxy groups leading to slower hydrolysis. Trifunctional aminosilanes like APTES are known to hydrolyze and self-condense almost instantaneously in aqueous solutions due to intramolecular catalysis by the amine group, often forming oligomers and gels. In contrast, monofunctional silanes lack the capacity for cross-linking, which dramatically improves the stability of the treating solution by preventing premature polymerization and precipitation. This allows for more controlled, reproducible surface reactions and significantly extends the usable lifetime of processing baths.

This ensures batch-to-batch consistency, reduces material waste from expired solutions, and enables more reliable manufacturing and research processes.

Monolayer vs. Multilayer Control

The number of reactive alkoxy groups directly dictates the final structure of the deposited film. Monoalkoxysilanes are explicitly noted to deposit as monolayers or incomplete monolayers. In contrast, trialkoxysilanes like APTES readily form multilayers, with reported thicknesses ranging from 1.8 nm (2-2.5 layers) up to several nanometers, indicating uncontrolled vertical polymerization. This difference is critical, as a true monolayer provides a well-defined surface with predictable properties, whereas a rough, polymeric multilayer introduces variability in surface energy, thickness, and functional group accessibility.

For applications like biosensors or nanoelectronics, a defined monolayer is essential for reproducible device fabrication and predictable performance.

Biosensor Surface Fabrication

The ability to form a well-defined monolayer with a controlled density of amine groups is critical for the consistent immobilization of bioreceptors (e.g., antibodies, enzymes). By preventing the formation of uncontrolled polymeric multilayers common with APTES, this compound ensures that each device has a comparable surface architecture, leading to lower device-to-device variability and more reliable analytical results.

Nanoparticle Functionalization

When modifying nanoparticles, the high reactivity of trifunctional silanes can cause irreversible aggregation due to inter-particle cross-linking. The monofunctional nature of 1-Propanamine, 3-(ethoxydimethylsilyl)- provides a more controlled reaction limited to the nanoparticle surface, improving the stability and monodispersity of the final functionalized nanomaterial suspension.

Microelectronics Passivation Layers

In microelectronics, thin, uniform, and defect-free organic layers are used for surface passivation and adhesion promotion. The controlled monolayer formation associated with this monofunctional silane prevents the creation of thick, irregular films that could compromise device performance, ensuring a uniform and structurally sound interface.