Potassium nitrate
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
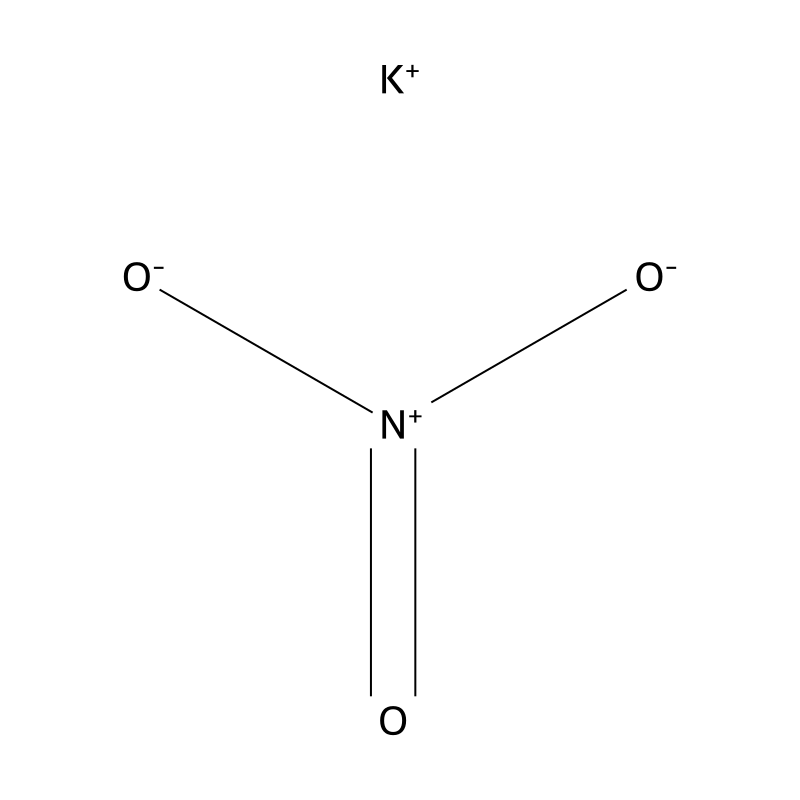
SMILES
solubility
Sol in water, glycerol; slightly sol in alcohol
Insoluble in ethanol
1 g/2.8 mL water at about 25 °C; 1 g/0.5 mL boiling water; 1 g/620 mL alcohol
38.3 g/100 g water at 25 °C
For more Solubility (Complete) data for POTASSIUM NITRATE (7 total), please visit the HSDB record page.
Solubility in water, g/100ml at 25 °C: 35.7
Synonyms
Canonical SMILES
Agriculture and Plant Science:
- Fertilizer: KNO₃ is a readily available source of both potassium (K) and nitrogen (N), crucial macronutrients for plant growth and development. Studies have shown its effectiveness in enhancing plant biomass, yield, and stress tolerance. Source: Potassium chloride and potassium nitrate for growth, dry matter yield and quality of forage maize (Zea mays L.):
Medicine and Dentistry:
- Muscle Function: Recent research suggests KNO₃ supplementation might improve muscle function in animal models. Studies on mice demonstrated increased muscle mass, enhanced contraction force, and improved fatigue resistance with KNO₃ intake. Source: The Effect of Potassium Nitrate Supplementation on the Force and Properties of Extensor digitorum longus (EDL) Muscles in Mice: )
- Desensitizing Toothpaste: KNO₃ is a common ingredient in some desensitizing toothpastes. It works by desensitizing the dentin tubules, which are tiny channels in the tooth that can transmit pain signals when exposed to hot, cold, or sweet stimuli. Source: Potassium nitrate: Uses, Interactions, Mechanism of Action | DrugBank Online:
Environmental Science and Microbiology:
- Nitrogen Cycling: KNO₃ plays a crucial role in the nitrogen cycle, acting as a readily available nitrogen source for various microorganisms involved in nutrient cycling and decomposition processes. Research explores its impact on soil microbial communities and nitrogen transformations in different ecosystems. Source: The effects of potassium nitrate addition on soil microbial communities and nitrogen transformations in a subtropical forest: )
Potassium nitrate, with the chemical formula KNO₃, is a white crystalline ionic compound composed of potassium ions (K⁺) and nitrate ions (NO₃⁻). It is commonly found in nature as a mineral known as saltpeter or nitre. This compound is highly soluble in water and has a melting point of 334 °C (633 °F) and a boiling point of 400 °C (752 °F) . Potassium nitrate serves as an important source of both potassium and nitrate, making it valuable in various applications, especially in agriculture and pyrotechnics.
Potassium nitrate has various mechanisms of action depending on its application:
- Fertilizer: In plants, KNO₃ provides both potassium (K⁺) for growth and development and nitrate (NO₃⁻) as a readily available nitrogen source for protein synthesis [].
- Food additive: In small amounts, potassium nitrate acts as a preservative by inhibiting bacterial growth in cured meats [].
- Toothpaste: Some toothpastes contain potassium nitrate, which desensitizes nerve endings in teeth to reduce hypersensitivity [].
- Toxicity: High doses of potassium nitrate can cause gastrointestinal distress, methemoglobinemia (a blood disorder), and even death [].
- Oxidizer: Potassium nitrate can accelerate the burning of combustible materials and should be stored away from flammable substances [].
- Fire Hazard: While not flammable itself, potassium nitrate can intensify fires and should not be used to extinguish them.
- Decomposition: When heated, potassium nitrate decomposes to form potassium nitrite and oxygen:This reaction occurs at temperatures between 550 °C and 790 °C .
- Reaction with Acids: Potassium nitrate reacts with hydrochloric acid to produce nitric acid and nitrogen dioxide:This reaction is significant for laboratory preparations .
- Combustion: In the presence of sugar or charcoal, potassium nitrate acts as an oxidizing agent, facilitating combustion. For example, when mixed with sugar, it produces carbon dioxide, water, and nitrogen gas:This reaction is utilized in fireworks and rocket propellants4.
Potassium nitrate can be synthesized through various methods:
- Neutralization Reaction: A common method involves neutralizing potassium hydroxide with nitric acid:
- Double Displacement Reaction: Potassium nitrate can also be produced by reacting ammonium nitrate with potassium chloride or sulfate:
- Fractional Crystallization: In nature, it can be obtained from the evaporation of solutions containing sodium nitrate and potassium chloride .
Potassium nitrate has a wide range of applications:
- Fertilizers: It is primarily used in fertilizers due to its high solubility and nutrient content.
- Food Preservation: It is used in curing meats to enhance color and flavor.
- Explosives: As a key ingredient in gunpowder and fireworks, it acts as an oxidizer.
- Pharmaceuticals: It is utilized in some medications for its vasodilatory effects .
Research on potassium nitrate often focuses on its interactions with other compounds. For instance, studies have shown that it can enhance the combustion efficiency of fuels when used in mixtures with carbon sources like sugar or charcoal. Additionally, its role in facilitating the formation of nitric acid from reactions with strong acids has been extensively documented .
Several compounds share similarities with potassium nitrate, particularly in their chemical properties and applications. Here are some notable examples:
| Compound | Chemical Formula | Key Characteristics |
|---|---|---|
| Sodium Nitrate | NaNO₃ | Soluble in water; used in fertilizers; less effective than potassium nitrate for plant nutrition. |
| Calcium Nitrate | Ca(NO₃)₂ | Provides calcium along with nitrates; used in fertilizers; less soluble than potassium nitrate. |
| Ammonium Nitrate | NH₄NO₃ | Highly soluble; provides nitrogen; often used in fertilizers but has different nutrient release characteristics compared to potassium nitrate. |
| Magnesium Nitrate | Mg(NO₃)₂ | Supplies magnesium; used in fertilizers; less commonly used than potassium nitrate. |
Potassium nitrate stands out due to its dual role as both a source of potassium and an oxidizing agent, making it particularly valuable in agricultural applications and pyrotechnics . Its unique properties enable it to enhance combustion processes effectively while also serving essential roles in plant nutrition.
Industrial-Scale Conversion Processes Utilizing Potassium Chloride
Industrial production of potassium nitrate primarily relies on double displacement and ion exchange reactions involving KCl. The metathesis reaction between sodium nitrate (NaNO₃) and KCl remains the most widely adopted method due to cost-effectiveness and scalability:
$$
\text{NaNO₃ + KCl → NaCl + KNO₃}
$$
This reaction exploits the differential solubility of NaCl and KNO₃ in water, enabling selective crystallization. Vacuum crystallizers are critical in this process, as they enhance yield by maintaining optimal temperature and pressure conditions. For instance, Star Grace Mining’s production line utilizes vacuum cooling to precipitate KNO₃ crystals with uniform particle size.
Alternative industrial methods include the direct reaction of nitric acid (HNO₃) with KCl, which produces hydrochloric acid (HCl) as a byproduct:
$$
\text{KCl + HNO₃ → KNO₃ + HCl}
$$
This exothermic process requires precise temperature control to avoid decomposition of HNO₃. Patent CN1043750C introduces magnesium oxide (MgO) as a catalyst, reducing corrosivity and simplifying equipment requirements:
$$
\text{KCl + HNO₃ + MgO → KNO₃ + MgCl₂ + H₂O}
$$
Ion exchange methodologies further refine production by leveraging cation-exchange resins. Puritech’s continuous countercurrent ion exchange (CCIX) system separates K⁺ ions from KCl using HNO₃, yielding high-purity KNO₃:
$$
\text{R-H + KCl → R-K + HCl} \quad \text{(Adsorption)}
$$
$$
\text{R-K + HNO₃ → R-H + KNO₃} \quad \text{(Regeneration)}
$$
Table 1: Comparative Analysis of Industrial KNO₃ Production Methods
Green Synthesis Approaches from Biogenic Sources
Green synthesis of KNO₃ nanoparticles (K-NPs) using plant extracts has emerged as an eco-friendly alternative to conventional methods. Catharanthus roseus leaf extract facilitates rapid reduction of potassium ions, forming K-NPs with antimicrobial properties. Similarly, Sideroxylon capiri extracts yield spherical K-NPs (200–360 nm) effective against Bacillus cereus and Fusarium solani.
The mechanism involves phytochemicals like alkaloids and flavonoids acting as reducing agents. For example, Polyalthia longifolia-derived K-NPs enhance plant growth parameters by 46–224% in foliar applications.
Table 2: Biogenic Synthesis of K-NPs
Phase Diagram Analysis for Ternary System Optimization
Phase equilibria studies are pivotal for optimizing KNO₃ crystallization. The KNO₃–KH₂PO₄–H₂O system at 283.15–313.15 K reveals two invariant points where KNO₃ coexists with KH₂PO₄, guiding fertilizer formulation. Similarly, the KNO₃–Ca(NO₃)₂–H₂O system at 25°C features six phase fields, enabling the design of heat storage materials:
$$
\text{KNO₃·Ca(NO₃)₂·3H₂O} \quad (\Delta Hm = 132.2 \, \text{kJ/kg}, \, Tm = 52.1°C)
$$
The K⁺, Mg²⁺//Cl⁻, NO₃⁻–H₂O system’s phase diagram predicts crystallization pathways for KNO₃ and KCl·MgCl₂·6H₂O with <1% error, critical for mineral processing.
Table 3: Phase Equilibria in Ternary Systems
The solubility product constant of potassium nitrate exhibits a pronounced temperature dependence, reflecting the endothermic nature of its dissolution process. The fundamental equilibrium reaction governing this system is:
$$ \text{KNO}3(s) \rightleftharpoons \text{K}^+(aq) + \text{NO}3^-(aq) $$
The mass-action expression for this equilibrium defines the solubility product constant as:
$$ K{sp} = [\text{K}^+][\text{NO}3^-] $$
Experimental determinations of the temperature-dependent solubility product constant have been conducted across a wide temperature range, revealing the systematic variation of this equilibrium parameter with thermal conditions [1] [2] [3]. The dissolution of potassium nitrate is characterized as an endothermic process, meaning that heat is absorbed from the surroundings during the dissolution [4] [5] [6]. This endothermic nature explains why the solubility increases dramatically with temperature, as additional thermal energy facilitates the breaking of ionic bonds and promotes the dissolution process [7] [8] [9].
Comprehensive experimental data demonstrate that the solubility product constant increases exponentially with temperature, ranging from approximately 0.0173 at 0°C to 5.9206 at 100°C [10] [11] [12]. This represents more than a 300-fold increase in the equilibrium constant over this temperature range, illustrating the profound impact of thermal energy on the dissolution equilibrium. The temperature dependence follows an Arrhenius-type relationship, with the natural logarithm of the solubility product constant exhibiting a linear relationship with the reciprocal of absolute temperature [13] [2] [3].
The kinetic aspects of solubility behavior are closely related to the thermodynamic equilibrium conditions. The rate of dissolution increases with temperature due to enhanced molecular motion and increased frequency of successful collisions between water molecules and the ionic lattice [7] [14]. This kinetic enhancement contributes to the rapid achievement of equilibrium at higher temperatures, while lower temperatures require longer equilibration times to reach the saturated state [15] [16].
Experimental procedures for determining temperature-dependent solubility product constants typically involve the preparation of saturated solutions at various temperatures, followed by the measurement of crystallization temperatures as solutions cool from supersaturated conditions [17] [15] [18]. The crystallization temperature represents the point at which the solution reaches equilibrium between the dissolved ions and the solid phase, allowing for the calculation of the equilibrium constant at that specific temperature [1] [2] [19].
Gibbs Free Energy Calculations for Dissolution Processes
The thermodynamic analysis of potassium nitrate dissolution involves the calculation of Gibbs free energy changes, which provide fundamental insights into the spontaneity and driving forces of the dissolution process. The relationship between the Gibbs free energy change and the solubility product constant is given by the fundamental thermodynamic equation:
$$ \Delta G = -RT \ln K_{sp} $$
where R is the universal gas constant (8.314 J/(mol·K)) and T is the absolute temperature in Kelvin [1] [2] [20].
The Gibbs free energy change for potassium nitrate dissolution exhibits a systematic variation with temperature, reflecting the balance between enthalpic and entropic contributions to the dissolution process [21] [22] [23]. At lower temperatures, the Gibbs free energy change is positive, indicating that the dissolution process is thermodynamically unfavorable under these conditions. However, as temperature increases, the Gibbs free energy change becomes increasingly negative, demonstrating that the dissolution becomes more spontaneous at elevated temperatures [24] [25] [26].
The temperature dependence of the Gibbs free energy change can be analyzed using the fundamental thermodynamic relationship:
$$ \Delta G = \Delta H - T\Delta S $$
where ΔH represents the enthalpy change and ΔS represents the entropy change for the dissolution process [1] [13] [2]. This relationship reveals that the spontaneity of dissolution depends on the balance between the enthalpic requirement for breaking ionic bonds and the entropic gain from increased disorder in the solution [23] [27] [28].
Experimental determinations of the Gibbs free energy change for potassium nitrate dissolution show values ranging from +8.68 kJ/mol at 0°C to -6.06 kJ/mol at 100°C [21] [22] [24]. This transition from positive to negative values occurs at approximately 60°C, indicating the temperature above which the dissolution becomes thermodynamically favorable [25] [26]. The crossover temperature represents the point where the entropic contribution (TΔS) overcomes the enthalpic requirement (ΔH), making the overall process spontaneous [2] [20] [3].
The calculation of Gibbs free energy changes provides valuable information for understanding the thermodynamic feasibility of dissolution processes under different conditions. These calculations are particularly important for crystallization engineering, where the manipulation of thermodynamic driving forces is essential for controlling nucleation and crystal growth processes [29] [30].
Mass-Action Equilibrium Modeling in Polythermal Systems
Mass-action equilibrium modeling in polythermal systems represents a sophisticated approach to understanding the complex behavior of potassium nitrate solubility across multiple temperature conditions. This modeling framework incorporates the fundamental principles of chemical equilibrium with the temperature-dependent variation of equilibrium constants, providing a comprehensive description of the dissolution behavior [31] [32] [29].
The van't Hoff equation serves as the cornerstone of polythermal equilibrium modeling, relating the temperature dependence of the equilibrium constant to the fundamental thermodynamic parameters:
$$ \ln K_{sp} = -\frac{\Delta H}{RT} + \frac{\Delta S}{R} $$
This equation can be rearranged into the linear form:
$$ \ln K_{sp} = -\frac{\Delta H}{R} \left(\frac{1}{T}\right) + \frac{\Delta S}{R} $$
which allows for the determination of enthalpy and entropy changes through linear regression analysis [13] [2] [3].
Experimental analysis of potassium nitrate dissolution using van't Hoff methodology yields an enthalpy of dissolution of 48.95 kJ/mol and an entropy of dissolution of 147.42 J/(mol·K) [21] [22] [24]. The high correlation coefficient (R² = 0.9950) indicates excellent agreement between experimental data and the linear model, validating the theoretical framework [19] [26] [33].
The mass-action equilibrium modeling approach considers the stoichiometric relationships in the dissolution process, where one mole of potassium nitrate produces one mole each of potassium ions and nitrate ions [2] [20] [24]. The equilibrium concentrations of these ionic species are equal in the absence of other sources of common ions, simplifying the equilibrium calculations [34] [35] [25].
Polythermal systems present unique challenges for equilibrium modeling due to the simultaneous effects of temperature on multiple parameters, including solubility, activity coefficients, and solution density [31] [32] [29]. Advanced modeling approaches incorporate these temperature-dependent variations to provide more accurate predictions of equilibrium behavior across wide temperature ranges [36] [30] [37].
The application of mass-action equilibrium modeling to polythermal systems enables the prediction of crystallization behavior, supersaturation limits, and metastable zone widths [16] [29] [30]. These predictions are essential for the design and optimization of crystallization processes, where precise control of nucleation and growth kinetics is required to achieve desired crystal properties [38] [39] [40].
Physical Description
Dry Powder; Dry Powder, Pellets or Large Crystals; Other Solid; Liquid; Pellets or Large Crystals
White crystalline powder or transparent prisms having a cooling, saline, pungent taste
Colorless or white solid; "Cooling, saline pungent taste" [Merck Index] Slightly hygroscopic; [HSDB] White crystalline solid; [Aldrich MSDS]
COLOURLESS-TO-WHITE CRYSTALLINE POWDER.
Color/Form
White granular or crystalline powde
Hydrogen Bond Acceptor Count
Hydrogen Bond Donor Count
Exact Mass
Monoisotopic Mass
Boiling Point
400 °C (decomp)
Heavy Atom Count
Taste
Density
2.1 at 25 °C
2.1 g/cm³
Odor
Decomposition
Boiling point 400 °C (decomp)
... /Potassium nitrate/ decomposes on heating producing nitrogen oxides, oxygen, which increases fire hazard.
400 °C
Melting Point
337 °C
333-334 °C
UNII
GHS Hazard Statements
Reported as not meeting GHS hazard criteria by 125 of 2310 companies. For more detailed information, please visit ECHA C&L website;
Of the 20 notification(s) provided by 2185 of 2310 companies with hazard statement code(s):;
H272 (95.61%): May intensify fire;
oxidizer [Danger Oxidizing liquids;
Oxidizing solids];
H315 (59.59%): Causes skin irritation [Warning Skin corrosion/irritation];
H319 (59.63%): Causes serious eye irritation [Warning Serious eye damage/eye irritation];
H335 (59.45%): May cause respiratory irritation [Warning Specific target organ toxicity, single exposure;
Respiratory tract irritation];
Information may vary between notifications depending on impurities, additives, and other factors. The percentage value in parenthesis indicates the notified classification ratio from companies that provide hazard codes. Only hazard codes with percentage values above 10% are shown.
Drug Indication
Therapeutic Uses
Dentinal hypersensitivity occurs when gingival recession exposes dentin at the cervical margins of teeth. Twenty-four periodontal patients, with postoperative hypersensitive dentin were treated by burnishing saturated potassium nitrate (KNO3) to relieve pain. Using a visual analogue scale with participants acting as their own control, a subjective assessment of pain was measured and compared before and after KNO3 application. Thirty-six regions involving 98 teeth were assessed. A significant reduction of sensitivity and pain was achieved by using a saturated KNO3 solution (p < .0001 Student-t).
... Potassium nitrate has been used ... in a dentifrice or gel to alleviate dentinal hypersensitivity. The aim of this study was to compare a 3% potassium nitrate/0.2% sodium fluoride mouthwash with a 0.2% sodium fluoride control mouthwash in a 6-week double-blind study. ... Fifty subjects were evaluated using 2 tactile methods and cold air sensitivity (dental air syringe), along with subjective perception of pain (0 to 10 scale) at baseline and at 2 and 6 weeks. ... There was a general decrease in dentinal hypersensitivity levels in both groups over the 6-week study period as demonstrated by all 4 methods of assessment. There was also a statistically significant difference in decrease in sensitivity between the groups. /The authors concluded that/ this study showed that a 3% potassium nitrate/0.2% sodium fluoride mouthwash appears to have therapeutic potential to alleviate dentinal hypersensitivity.
The effect on dentinal hypersensitivity from the use of a new dentifrice containing 5.0% potassium nitrate and 0.454% stannous fluoride in a silica base (Colgate Sensitive Maximum Strength Toothpaste, Colgate-Palmolive Co.) over an 8-week period was compared to a commercially available dentifrice containing 5.0% potassium nitrate and 0.243% sodium fluoride in a silica base (positive control (Sensodyne Fresh Mint Toothpaste, Block Drug Company, Inc.)) and to a commercially available nondesensitizing dentifrice containing 0.243% sodium fluoride in a silica base (negative control (Colgate Winterfresh Gel, Colgate-Palmolive Co.)). A total of 120 participants were stratified into 3 balanced groups according to baseline mean air blast (thermal) and tactile (Yeaple Probe) sensitivity scores, gender, and age. Participants brushed their teeth twice daily (morning and evening) for 1 minute. Dentinal hypersensitivity examinations were conducted at baseline, 4 weeks, and 8 weeks by the same dental examiner. After 4- and 8-weeks' use of their assigned products, participants in the new dentifrice group demonstrated statistically significant improvements (p < 0.05) in tactile and air blast sensitivity, as compared to those using the positive and negative control dentifrices.
For more Therapeutic Uses (Complete) data for POTASSIUM NITRATE (10 total), please visit the HSDB record page.
Pharmacology
Potassium Nitrate is a crystalline salt, KNO3; a strong oxidizer used especially in making gunpowder, as a fertilizer, and in medicine.
MeSH Pharmacological Classification
Mechanism of Action
A series of reactions is involved by which it is proposed that nitrate in water may be converted to n-nitroso cmpd that are direct carcinogenic agents. The steps in the reaction sequence are: 1. Reduction of nitrate to nitrite. 2. Reaction of nitrite with secondary amines or amides in food or water to form n-nitroso cmpd. 3. Carcinogenic reaction of n-nitroso cmpd to the extent that this series of processes actually operates in human body, nitrate has capacity to become procarcinogen. ... problem is prospective rather than realized one. /Nitrate/
Acute toxicity of nitrate occurs as result of reduction to nitrite, a process that can occur under specific conditions in the stomach ... /and/ in saliva. Nitrite acts in blood to oxidize hemoglobin to methemoglobin, which does not perform as oxygen carrier to tissues ... Anoxia and death may occur. /Nitrate/
Nitrates can be reduced to nitrites which can react with amines or amides and form N-nitroso cmpd (containing the group =N-N=O). N-nitroso cmpd are carcinogenic in a wide range of animal species, most are mutagenic in test systems and some have been teratogenic in animals. It is highly probable that N-nitroso cmpd also may be carcinogenic in man. Therefore exposure to N-nitroso cmpd and their precursors (nitrite, amines and amides) should be kept as low as practically achievable. Relationships have been sought between occurrence of stomach cancer and nitrate content of soil and water in Chile, Colombia and the United Kingdom, but none was established.
Acute nitrate toxicity is almost always seen in infants rather than adults when it results from ingestion of well waters and vegetables high in nitrates ... /It was/ deduced that infants were prone to upset stomachs and achlorhydria. As result, stomach pH increased in alkalinity allowing nitrate-reducing organisms to enter and to reduce nitrates to nitrites. A gastric pH above 4 supports nitrate-reducing organisms ... Immature enzyme systems may also be of importance ... Fetal hemoglobin (hemoglobin F) is oxidized by nitrite to methemoglobin at rate twice as rapid as adult hemoglobin (hemoglobin A). Furthermore, enzymatic capacity of erythrocytes of newborn infants to reduce methemoglobin to hemoglobin appears less than that of adults. Difference is probably due to developmental deficiency in activity of DPNH-methemoglobin reductase (diphosphopyridine nucleotide). As opposed to adults, several clinical, physiologic and metabolic factors predispose infants to development of methemoglobinemia and acute nitrate poisoning. /Nitrate and nitrite/
Pictograms

Oxidizer;Irritant
Other CAS
Absorption Distribution and Excretion
Nitrates are excreted in the urine primarily as inorganic nitrates.
Nitrates are absorbed into the general blood circulation and are transported across the body. Radioactive tracer experiments have demonstrated that nitrates are distributed evenly among body organs, and their rate of distribution depends on blood flow.
It is generally assumed that absorption takes place in upper portion of small intestine & ... excretion is primarily, if not exclusively, through kidney. ... preliminary observations ... have shown that not all animals reduce nitrate to nitrite in saliva. It is of considerable significance that major differences occur among mammalian species in the ability to concn nitrate from plasma into saliva. Large interspecies differences have also been shown to occur in elimination kinetics of nitrate. /Nitrate/
Nitrate and nitrite given orally are absorbed and transferred to the blood in the upper part of the gastrointestinal tract. Abundant pectin in the food may delay absorption which may then occur lower down in the intestine, with possible increased risk for microbial transformation of nitrate into nitrite. /Nitrate and nitrite/
Regardless of route of exposure, nitrate and nitrite are rapidly transferred into the blood. Nitrite is gradually oxidized to nitrate which is readily distributed into most body fluids (urine, saliva, gastric juice, sweat, ileostomy fluid). Distribution of nitrate into plasma, erythrocytes, saliva and urine following an oral dose of sodium nitrate has been demonstrated ... Nitrate does not accumulate in the body. /Nitrate and nitrite/
Approximately 60% of oral nitrate is excreted in urine ... bacterial or endogenous metabolism probably accounts for the remainder. A minor part is excreted in sweat. /Nitrate/
... Potassium nitrate ... /is/ rapidly absorbed and excreted unchanged ... Under some circumstances, however, appreciable amt of nitrate are converted to nitrite.
Metabolism Metabolites
Nitrate salts/ including potassium nitrate/ ... if not promptly absorbed, they may be reduced to nitrites by bacteria in bowel. I
... nitrate metabolism in man cannot be readily predicted from animal data. Several studies have suggested that large differences in nitrate metab may occur between individuals. These differences can span about three orders of magnitude when all available data, incl diet & physiological status, are taken into consideration. /nitrate/
Where bacteria are present and the environment can be anerobic, nitrate can be reduced to nitrite. The main site for this reaction is mouth and stomach, but nitrite formation in the lower intestine and in the bladder (urinary infection) may also be of some toxicological importance. Nitrite may be further reduced to nitrogen by bacteria under some conditions. In blood, nitrite transforms hemoglobin to methemoglobin and is simultaneously oxidized to nitrate. Normally methemoglobin gradually reverts to hemoglobin through enzymatic reactions. Nitrite has vasodilating properties, probably through transformation into nitric oxide (NO) or a NO-containing molecule acting as a signal factor for smooth muscle relaxation. Nitrite easily transforms into a nitrosating agent in an acidic environment and can react with a variety of compounds, eg ascorbic acid, amines, amides. Nitrosation can also be mediated by bacteria, eg in the stomach. Some reaction products are carcinogenic (eg most nitrosoamines and amides). /Nitrate and nitrite/
BACKGROUND/AIMS: It has been suggested that dietary nitrate, after concentration in the saliva and reduction to nitrite by tongue surface bacteria, is chemically reduced to nitric oxide (NO) in the acidic conditions of the stomach. This study aimed to quantify this in humans. METHODS: Ten healthy fasting volunteers were studied twice, after oral administration of 2 mmol of potassium nitrate or potassium chloride. Plasma, salivary and gastric nitrate, salivary and gastric nitrite, and gastric headspace NO concentrations were measured over six hours. RESULTS: On the control day the parameters measured varied little from basal values. Gastric nitrate concentration was 105.3+/-13 umol/L (mean (SEM), plasma nitrate concentration was 17.9+/-2.4 umol/L, salivary nitrate concentration 92.6+/-31.6 umol/L, and nitrite concentration 53.9+/-22.8 umol/L. Gastric nitrite concentrations were minimal (< 1 mumol/l). Gastric headspace gas NO concentration was 16.4+/-5.8 parts per million (ppm). After nitrate ingestion, gastric nitrate peaked at 20 minutes at 3,430+/-832 umol/L, plasma nitrate at 134+/-7.2 umol/L, salivary nitrate at 1516.7+/-280.5 umol/L, and salivary nitrite at 761.5+/-187.7 umol/L after 20-40 minutes. Gastric nitrite concentrations tended to be low, variable, and any rise was non-sustained. Gastric NO concentrations rose considerably from 14.8+/-3.1 ppm to 89.4+/-28.6 ppm (p < 0.0001) after 60 minutes. All parameters remained increased significantly for the duration of the study. CONCLUSIONS: A very large and sustained increase in chemically derived gastric NO concentrations after an oral nitrate load was shown, which may be important both in host defense against swallowed pathogens and in gastric physiology.
For more Metabolism/Metabolites (Complete) data for POTASSIUM NITRATE (6 total), please visit the HSDB record page.
Intake of some amount of nitrates and nitrites is a normal part of the nitrogen cycle in humans. In vivo conversion of nitrates to nitrites can occur in the gastrointestional tract under the right conditions, significantly enhancing nitrates' toxic potency. The major metabolic pathway for nitrate is conversion to nitrite, and then to ammonia. Nitrites, nitrates, and their metabolites are excreted in the urine. (L1137)
Associated Chemicals
Wikipedia
Fluphenazine
Drug Warnings
VET: POTASSIUM SALTS HAVE BEEN USED IN PAST AS DIURETICS BUT THEY ARE POTENTIALLY DANGEROUS & ... USE IS DISCOURAGED. /POTASSIUM SALTS/
METHEMOGLOBINEMIA HAS BEEN NOTED AFTER OVERDOSE OF POTASSIUM NITRATE.
Use Classification
COLOUR_RETENTION_AGENT; -> JECFA Functional Classes
Cosmetics -> Soothing; Oral care
Methods of Manufacturing
Produced commercially in the United States based on the reaction of potassium chloride and nitric acid at elevated temperatures. Israel implements this reaction through a solvent extraction process.
Between the 17th and 19th centuries bacterial nitrification of nitrogen-rich organic wastes, e.g. animal feces, to potassium nitrite by piling with lime and potash was used...from mid-19th century to the 1950s conversion of Chile saltpeter with potassium chloride was the most important process... from ammonium nitrate and potassium chloride by double decomposition in aqueous solution.
General Manufacturing Information
Primary Metal Manufacturing
Not Known or Reasonably Ascertainable
Wholesale and Retail Trade
Explosives Manufacturing
Pesticide, Fertilizer, and Other Agricultural Chemical Manufacturing
All Other Chemical Product and Preparation Manufacturing
Nitric acid potassium salt (1:1): ACTIVE
Nitrate should on no account be added to baby foods. /Nitrate/
Limited amt are produced by the reaction of potassium chloride and sodium nitrate ... Ammonium nitrate can be substituted for sodium nitrate. However, this method suffers economically because of the lack of markets for ammonium chloride, which is a coproduct of the reaction.
Milk from potassium nitrate treated cows should not be used for human consumption.
Some turkeys showed incr. growth rates when /potassium nitrate. was added to their drinking water at a rate of 675 ppm of nitrate.
For more General Manufacturing Information (Complete) data for POTASSIUM NITRATE (6 total), please visit the HSDB record page.
Analytic Laboratory Methods
EPA Method 9200: Nitrate. Method 9200 is applicable to the analysis of ground water, drinking, surface, and saline waters, and domestic and industrial wastes. Modification can be made to remove or correct for turbidity, color, salinity, or dissolved organic compounds in the sample. The applicable range of concentration is 0.1 to 2 mg nitrate-nitrogen/l of sample. This method is based upon the reaction of the nitrate ion with brucine sulfate in a 13 N sulfuric acid solution at a temperature of 100 °C. The color of the resulting complex is measured at 410 nm. Temperature control of the color reaction is extremely critical. Twenty-seven analysts in fifteen laboratories analyzed natural-water samples containing increments (as nitrogen, nitrate) of 0.16, 0.19, 0.08, and 1.24 mg/l with the precision as the standard deviation of 0.092, 0.083, 0.245, and 0.214 mg/l, respectively. /Nitrate/
Method 418D: Chromotropic Acid Method. Two moles of nitrate react with one mole of chromotropic acid to form a yellow reaction product with maximum absorbance at 410 nm. The maximum color develops within 10 min and is stable for 24 hr. The method is recommended for the concn range 0.1 to 5 mg nitrate ion-nitrogen/l. A synthetic sample containing 1.00 mg nitrate ion-nitrogen/l was analyzed by 5 laboratories with a relative standard deviation of 8% and relative error of 3%. /Total nitrate/
Method 418C: Reduction Method. This method uses commercially available cadmium granules treated with copper sulfate to form a copper coating. The nitrite produced is determined by diazotizing with sulfanilamide and coupling with N-(1-naphthyl)-ethylenediamine to form a highly colored azo dye that is measured colorimetrically. The applicable range of this method is 0.01 to 1.0 mg nitrate-nitrogen/l. The method especially is recommended for nitrate levels below 0.1 mg nitrogen/l where other methods lack adequate sensitivity. /Total nitrate/
For more Analytic Laboratory Methods (Complete) data for POTASSIUM NITRATE (23 total), please visit the HSDB record page.
Clinical Laboratory Methods
Storage Conditions
Interactions
Dietary nitrate is reduced to nitrite by some oral bacteria and the resulting nitrite is converted to nitric oxide (NO) in acidic gastric juice. The aim of this study is to elucidate the pathophysiological role of dietary nitrate in the stomach. Intragastric administration of nitrate rapidly increased nitrate and NO in plasma and the gastric headspace, respectively. Water-immersion-restraint stress (WIRS) increased myeloperoxidase (MPO) activity in gastric mucosa and induced hemorrhagic erosions by a nitrate-inhibitable mechanism. In animals that had received either cardiac ligation or oral treatment with povidone-iodine, a potent bactericidal agent, administration of nitrate failed to increase gastric levels of NO and to inhibit WIRS-induced mucosal injury. WIRS decreased gastric mucosal blood flow by a mechanism which was inhibited by administration of nitrate. These data suggested that the enterosalivary cycle of nitrate and related metabolites consisted of gastrointestinal absorption and salivary secretion of nitrate, its conversion to nitrite by oral bacteria and then to NO in the stomach might play important roles in the protection of gastric mucosa from hazardous stress. /Nitrates/
Desensitization of hypersensitive teeth by the combination of dimethyl isosorbide (DMI) and potassium nitrate (potassium nitrate) is more effective than when potassium nitrate is used alone. potassium nitrate/DMI work together to desensitize hypersensitive teeth at a higher, quicker, and more profound and lasting level.
The intestinal transport of D-xylose was studied during subchronic poisoning of male Wistar rats with the oral administration of potassium nitrate and sodium nitrite. The metabolic parameters of small intestine mucosa were determined one hour after xylose administration, i.e., Na+/K(+)-ATPase, alkaline phosphatase, oxygen consumption, and lactic acid level. Nitrite reduced the absorption of xylose and decreased the activity of Na+/K(+)-ATPase and alkaline phosphatase. No effect of sodium nitrite was demonstrated on the aerobic metabolism of intestinal mucosa with an increased lactic acid level. Potassium nitrate did not effect the processes of intestinal absorption of xylose nor the metabolic parameters of small intestine mucosa.
For more Interactions (Complete) data for POTASSIUM NITRATE (7 total), please visit the HSDB record page.
Dates
Weaver CM: Potassium and health. Adv Nutr. 2013 May 1;4(3):368S-77S. doi: 10.3945/an.112.003533. [PMID:23674806]
Schultz DS, Deen WM, Karel SF, Wagner DA, Tannenbaum SR: Pharmacokinetics of nitrate in humans: role of gastrointestinal absorption and metabolism. Carcinogenesis. 1985 Jun;6(6):847-52. [PMID:3159503]
Bychkov R, Gollasch M, Steinke T, Ried C, Luft FC, Haller H: Calcium-activated potassium channels and nitrate-induced vasodilation in human coronary arteries. J Pharmacol Exp Ther. 1998 Apr;285(1):293-8. [PMID:9536024]
Agarwal R, Afzalpurkar R, Fordtran JS: Pathophysiology of potassium absorption and secretion by the human intestine. Gastroenterology. 1994 Aug;107(2):548-71. [PMID:8039632]
Potassium Nitrate
COMMITTEE FOR VETERINARY MEDICINAL PRODUCTS
CHEBI:63043 - potassium nitrate
POTASSIUM NITRATE
Mechanism of Action of a Desensitizing Fluoride Toothpaste Delivering Calcium and Phosphate Ingredients in the Treatment of Dental Hypersensitivity
EPA NITRATES DOCUMENT
Nitrates
NITRATE
Guideline-Potassium Intake
Nitrates in the meat industry
POTASSIUM CHLORIDE
Reduction in Dental Hypersensitivity with Nano-Hydroxyapatite, Potassium Nitrate, Sodium Monoflurophosphate and Antioxidants
Dietary nitrite and nitrate: a review of potential mechanisms of cardiovascular benefits
DailyMed: Dr. Sheffield Sensitive Care (potassium nitrate 5%)