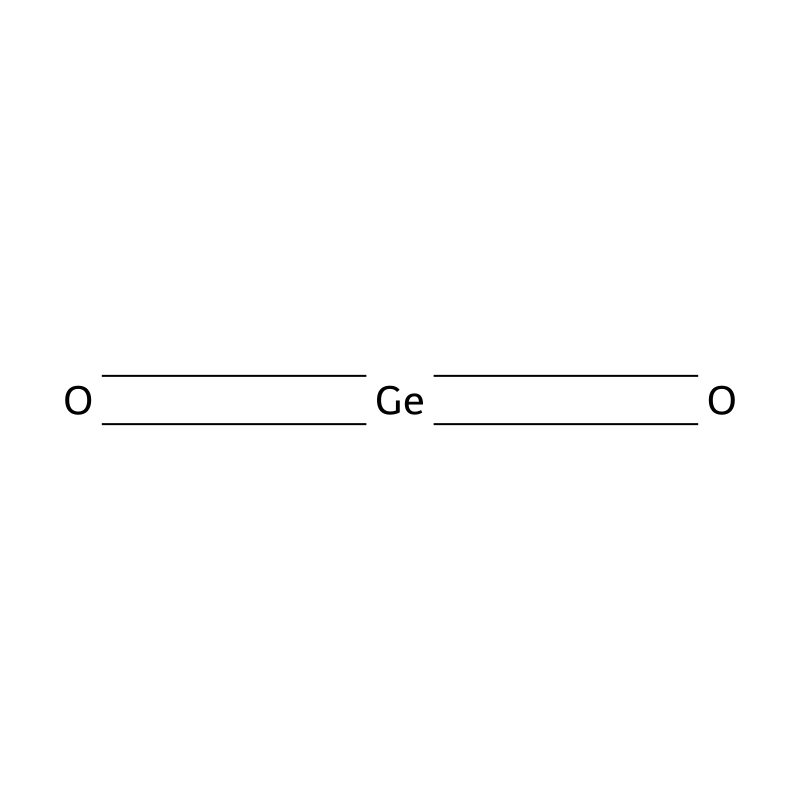
Germanium dioxide

Optics:

• High Refractive Index: GeO₂ possesses a high refractive index, making it ideal for creating lenses and other optical components. This property allows for efficient light manipulation and focusing capabilities.
• Infrared Transparency: GeO₂ is transparent to infrared radiation, making it suitable for windows and lenses in instruments like night vision goggles and infrared cameras.

Electronics:

• Substrate Material: Due to its stability and excellent electrical properties, GeO₂ is used as a substrate material for growing thin films of various semiconductors. These thin films are crucial components in transistors, solar cells, and other electronic devices.
• Gas Sensors: GeO₂ exhibits unique electrical conductivity changes upon exposure to specific gases. This makes it a promising material for developing gas sensors capable of detecting various pollutants and environmental markers.

Biomaterials:

• Antimicrobial Properties: Recent research suggests that GeO₂ nanoparticles may possess antimicrobial properties, potentially inhibiting the growth of certain bacteria and fungi.
• Biocompatibility and Potential Biomedical Applications: Studies exploring the biocompatibility of GeO₂ show promising results, indicating its potential for use in dental implants, bone repair materials, and drug delivery systems.

Neuroscience Research:

• Potential Role in Neurodegenerative Diseases: Pre-clinical studies using GeO₂ nanoparticles reveal their potential to mitigate Alzheimer's disease (AD) by reducing oxidative stress and regulating specific biomarkers associated with the disease.
• Further Research Needed: While these findings are encouraging, further research is necessary to fully understand the mechanisms of action and potential long-term effects before considering GeO₂ nanoparticles for therapeutic applications in AD.

Germanium dioxide, with the chemical formula $\text{GeO}_2$, is an oxide of germanium, a metalloid with atomic number 32. It exists in two primary forms: crystalline and amorphous. The crystalline form is typically found in nature as the mineral argyrodite, while the amorphous form can be produced through rapid cooling of molten germanium dioxide or by

Germanium dioxide is generally considered to be a low-hazard material []. However, some safety precautions should still be considered:

• Inhalation: Inhalation of germanium dioxide dust can irritate the respiratory tract [].
• Skin and eye contact: Direct contact can cause skin and eye irritation [].
• Chronic exposure: Animal studies suggest potential reproductive effects from chronic exposure to germanium dioxide dust [].

Germanium dioxide can be synthesized through various methods:

• Direct Oxidation: Heating elemental germanium in the presence of oxygen.
• Hydrolysis of Germanium Compounds: For example, hydrolyzing germanium tetrachloride.
• Thermal Decomposition: Heating germanium sulfide or other germanium compounds to produce germanium dioxide .

Studies on the interactions of germanium dioxide with various substances reveal its reactivity profile:

• It reacts with strong acids and bases but is generally stable under normal conditions.
• Incompatibility with strong oxidizing agents has been noted, leading to potential hazards during handling .
• Research into its ecological impact shows that it can be toxic to certain aquatic life forms, particularly diatoms, indicating environmental considerations for its use .

Several compounds share similarities with germanium dioxide. Here are some notable comparisons:

Germanium dioxide stands out due to its unique optical properties and applications in semiconductor technology, which differentiate it from these similar compounds. Its ability to function effectively at infrared wavelengths makes it particularly valuable in specialized optical applications not typically served by silicon or titanium dioxides .