Home / Products / Electronic Materials / Self Assembly & Contact Printing

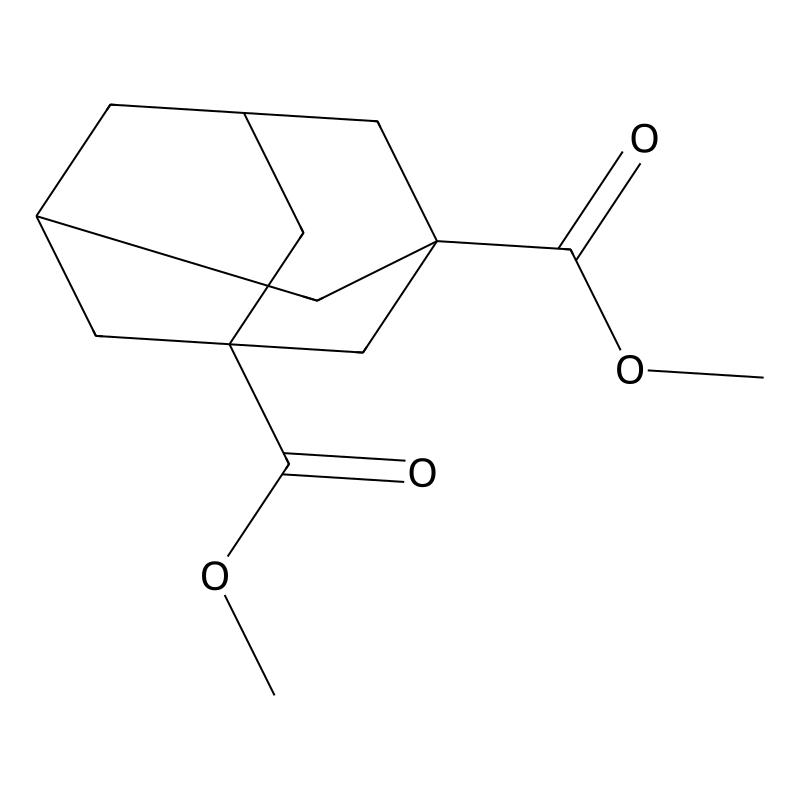
Dimethyl 1,3-adamantanedicarboxylate

Name: Dimethyl 1,3-adamantanedicarboxylate
Brand: Smolecule
SKU: S707799
Rating: 5 (9 reviews)

Catalog No.

S707799

CAS No.

1459-95-6

M.F

C14H20O4

M. Wt

252.31 g/mol

Availability

In Stock

* This item is exclusively intended for research purposes and is not designed for human therapeutic applications or veterinary use.

3. Specification
4. Others

General Information

CAS Number

1459-95-6

Product Name

Dimethyl 1,3-adamantanedicarboxylate

IUPAC Name

dimethyl adamantane-1,3-dicarboxylate

Molecular Formula

C14H20O4

Molecular Weight

252.31 g/mol

InChI

InChI=1S/C14H20O4/c1-17-11(15)13-4-9-3-10(5-13)7-14(6-9,8-13)12(16)18-2/h9-10H,3-8H2,1-2H3

InChI Key

YXMDGBXGJKYMQL-UHFFFAOYSA-N

SMILES

COC(=O)C12CC3CC(C1)CC(C3)(C2)C(=O)OC

Canonical SMILES

COC(=O)C12CC3CC(C1)CC(C3)(C2)C(=O)OC

Scientific Research Applications

Organic Synthesis:

Dimethyl 1,3-adamantanedicarboxylate (DMAD) serves as a valuable building block in organic synthesis due to its unique structure and chemical properties. The presence of the two ester groups allows for various chemical transformations, including:

Hydrolysis: Cleavage of the ester bonds using water or a base can generate 1,3-adamantanedicarboxylic acid, a versatile intermediate for further functionalization [].
Decarboxylation: Removal of the carboxyl groups under specific conditions can lead to the formation of 1,3-dimethyladamantane, a useful precursor for the synthesis of other adamantane derivatives [].
Alkylation: The ester groups can be alkylated using various reagents, enabling the introduction of desired functional groups onto the adamantine core [].

These transformations make DMAD a versatile building block for the synthesis of complex organic molecules, including pharmaceuticals, fine chemicals, and functional materials.

Medicinal Chemistry:

Limited research suggests the potential application of DMAD in medicinal chemistry. Studies have explored its:

Antiviral activity: DMAD exhibited antiviral activity against certain viruses, including the influenza virus, in preliminary studies []. However, further research is needed to determine its effectiveness and potential mechanisms of action.
Antibacterial activity: Some studies have reported antibacterial activity of DMAD against specific bacterial strains []. However, similar to antiviral activity, further investigation is necessary to assess its potential and develop effective therapeutic strategies.

Material Science:

Recent research indicates potential applications of DMAD in material science. Studies have investigated its use in the development of:

Organic light-emitting diodes (OLEDs): DMAD derivatives have been explored as potential host materials for OLEDs due to their desirable photophysical properties [].
Liquid crystals: Research suggests that DMAD can be used as a precursor for the synthesis of novel liquid crystals with specific properties [].