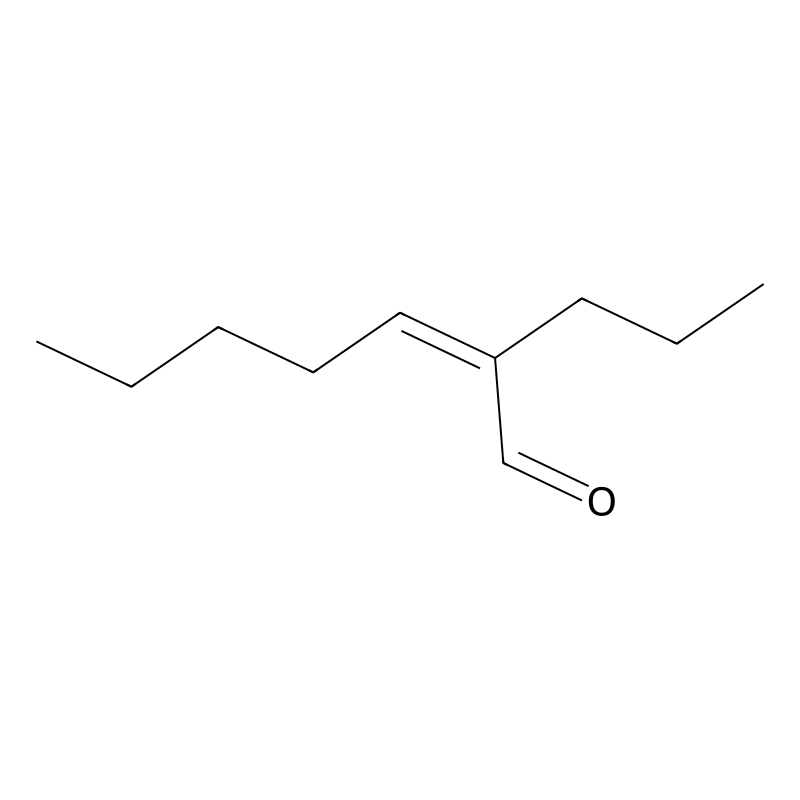
2-Propylhept-2-enal
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Synonyms
Canonical SMILES
Isomeric SMILES
Potential Source for Bioactive Compounds
One area of research focuses on the presence of 2-Propyl-2-heptenal as a natural product found in the plant Plectranthus glabratus. This suggests the possibility that it plays a role in the plant's biological processes or defense mechanisms. Further research into its isolation and potential bioactivity could lead to the discovery of new therapeutic agents [PubChem: 2-Propyl-2-heptenal, National Institutes of Health, ].
2-Propylhept-2-enal is an organic compound with the molecular formula and a molecular weight of approximately 154.25 g/mol. It is classified as an unsaturated aldehyde, characterized by the presence of both a double bond and an aldehyde functional group. The compound appears as a colorless to pale yellow liquid with a waxy texture and has a distinctive odor, which makes it valuable in the fragrance industry. Its structure includes a propyl group attached to a heptenal backbone, specifically at the second carbon position, which contributes to its unique chemical properties and reactivity .
- Information on the safety hazards of 2-Propyl-2-heptenal is limited. As with most organic compounds, it is advisable to handle it with care using appropriate personal protective equipment in a well-ventilated laboratory environment.
- Oxidation: The aldehyde group can be oxidized to form corresponding carboxylic acids.
- Reduction: It can be reduced to form alcohols, such as 2-propylheptanol.
- Aldol Condensation: It can undergo aldol condensation reactions, leading to the formation of larger carbon chains and various derivatives .
- Addition Reactions: The double bond in 2-propylhept-2-enal can undergo electrophilic addition reactions, allowing for the introduction of various functional groups .
The synthesis of 2-propylhept-2-enal typically involves the following methods:
- Aldol Condensation: A common synthetic route involves the self-condensation of valeraldehyde under basic conditions, often using sodium hydroxide or titanium dioxide as catalysts. This reaction leads to the formation of 2-propylhept-2-enal through dehydration of intermediates .
- Hydroformylation: Another method includes hydroformylation of alkenes followed by reduction, which can yield various aldehydes including 2-propylhept-2-enal .
- Oxo Process: The oxo process, involving the reaction of alkenes with carbon monoxide and hydrogen in the presence of a catalyst, can also be utilized for producing this compound .
Due to its unique properties, 2-propylhept-2-enal finds applications in several industries:
- Fragrance Industry: It is used as an intermediate in the production of perfumes due to its pleasant aroma.
- Plasticizers: The compound serves as an intermediate for producing plasticizers that enhance the flexibility and durability of plastics.
- Chemical Synthesis: It is utilized in organic synthesis for creating other chemical compounds and intermediates .
Interaction studies involving 2-propylhept-2-enal primarily focus on its reactivity with other chemical species. For instance, its behavior in aldol condensation reactions has been extensively studied to optimize conditions for higher yields and selectivity towards desired products. Furthermore, investigations into its interactions with biological systems are ongoing to explore potential therapeutic applications or toxicological effects .
When comparing 2-propylhept-2-enal with similar compounds, several notable compounds emerge:
| Compound Name | Structure Type | Key Features |
|---|---|---|
| 2-Ethylhexenal | Unsaturated Aldehyde | Similar chain length; used in fragrances |
| 3-Methylhexenal | Unsaturated Aldehyde | Different position of double bond; flavoring agent |
| 4-Methylpentenal | Unsaturated Aldehyde | Shorter chain; used in synthetic pathways |
Uniqueness
What sets 2-propylhept-2-enal apart from these similar compounds is its specific structural configuration that allows for distinct reactivity patterns and applications, particularly in fragrance formulation and plasticizer production. Its unique odor profile also contributes to its desirability in perfumery compared to other aldehydes.
Aldol Condensation Strategies
Aldol condensation remains the primary route for synthesizing 2-propylhept-2-enal, leveraging both homogeneous and heterogeneous catalytic systems.
Homogeneous Catalysis Systems (NaOH, NaOEt)
Homogeneous bases like NaOH and NaOEt facilitate aldol condensation of aldehydes (e.g., pentanal) via enolate formation. Key steps include:
- Deprotonation: NaOH generates enolate ions from aldehydes at 80–120°C.
- Nucleophilic Attack: Enolates attack electrophilic carbonyl carbons, forming β-hydroxyaldehyde intermediates.
- Dehydration: Elimination of water yields α,β-unsaturated aldehydes like 2-propylhept-2-enal.
Table 1: Performance of Homogeneous Catalysts
| Parameter | NaOH (80–120°C) | NaOEt (Ethanol Solvent) |
|---|---|---|
| Conversion (%) | >90 | 85–92 |
| Selectivity (%) | 75–88 | 78–90 |
| Byproduct Formation | <10% (branched isomers) | <8% (oligomers) |
Drawbacks include catalyst neutralization requirements and poor recyclability, driving interest in heterogeneous alternatives.
Heterogeneous Catalysis Systems (Na₂O/Al₂O₃)
Solid bases like Na₂O/Al₂O₃ enhance sustainability and selectivity:
- Mechanism: Surface basic sites deprotonate aldehydes, while Al₂O₃’s mesoporous structure stabilizes transition states.
- Optimized Conditions: 120°C, N₂ atmosphere, and 10 h reaction time achieve >95% conversion with <5% byproducts.
Table 2: Heterogeneous vs. Homogeneous Catalysts
| Metric | Na₂O/Al₂O₃ | NaOH |
|---|---|---|
| Temperature (°C) | 120 | 80–120 |
| Reaction Time (h) | 10 | 4–6 |
| Catalyst Reuse (%) | >90 | Not feasible |
| Energy Efficiency | High | Moderate |
Mixed oxides (e.g., Mg–Al, Zn–Al) further improve selectivity by tuning acid-base site ratios.
Hydroformylation-Oxo Synthesis
Hydroformylation of alkenes provides an alternative route to 2-propylhept-2-enal precursors.
Rhodium-Catalyzed Alkene Hydroformylation
Rhodium complexes (e.g., Rh(acac)(CO)₂) convert 1-butene to pentanal under syngas (H₂/CO):
- Conditions: 70–100°C, 1–3 MPa, ligand-to-Rh ratios of 10:1.
- Mechanism: Alkene insertion into Rh–H bonds, followed by CO insertion and reductive elimination.
Table 3: Rh-Catalyzed Hydroformylation Performance
| Ligand | n/iso Selectivity | TOF (h⁻¹) |
|---|---|---|
| P(NC₄H₄)₃ | 32:1 | 800 |
| PPh₃ | 8:1 | 667 |
Selectivity Control in Branched Aldehyde Formation
Selectivity hinges on ligand electronics and steric effects:
- Electron-Donating Ligands: Increase linear aldehyde yield (e.g., n-pentanal).
- Bimetallic Systems: Ru–Ni/Al₂O₃ enhances hydrogen spillover, favoring saturated aldehydes.
Catalytic Hydrogenation of Precursors
2-Propylhept-2-enal is hydrogenated to 2-propylheptanol, a plasticizer precursor.
Ni-Cr-K/Al₂O₃ Catalyst Optimization
Ni-based catalysts achieve >95% conversion of 2-propylhept-2-enal:
- Optimal Loading: 7.3 wt% Ni balances activity and selectivity.
- Support Effects: Al₂O₃’s acidity stabilizes Ni⁰ particles, preventing sintering.
Table 4: Hydrogenation Performance
| Catalyst | Conversion (%) | Selectivity (%) |
|---|---|---|
| Ni/Al₂O₃ (7.3 wt%) | 99 | 92 |
| Ni-Cr-K/Al₂O₃ | 98 | 94 |
Kinetic and Thermodynamic Parameters
Hydrogenation Pathways
Double Bond vs. Carbonyl Group Reactivity
2-Propylhept-2-enal contains both a conjugated double bond and a carbonyl group, presenting competing reaction sites for hydrogenation processes [1] [2] [3]. The selective reduction of carbon-carbon double bonds versus carbonyl groups in α,β-unsaturated aldehydes has been identified as a challenging problem in organic synthesis, particularly for compounds with extended alkyl chains like 2-propylhept-2-enal [10].
The reactivity hierarchy in 2-propylhept-2-enal hydrogenation follows established patterns for α,β-unsaturated carbonyl compounds [9] [10]. Under standard hydrogenation conditions using supported nickel-chromium-potassium catalysts, the carbonyl group demonstrates higher reactivity than the conjugated double bond [9]. Temperature-programmed reduction studies reveal that 2-propylhept-2-enal conversion exceeds 99% with selectivity toward 2-propyl heptanol reaching approximately 95% under optimal conditions of 4.0 megapascals pressure, 403 Kelvin temperature, and liquid hourly space velocity of 1.0 per hour [9].
The preferential carbonyl reduction occurs through a mechanism involving coordination of the aldehyde oxygen to the metal surface, followed by hydrogen transfer to the carbon atom [9] [13]. This pathway is thermodynamically favored due to the stronger metal-oxygen interaction compared to the π-coordination of the carbon-carbon double bond [13]. The saturated aldehyde intermediate (2-propylheptanal) formation remains minimal under standard reaction conditions, indicating efficient subsequent reduction to the alcohol product [9].
| Reaction Parameter | Optimal Value | Conversion (%) | Selectivity to 2-Propyl Heptanol (%) |
|---|---|---|---|
| Temperature | 403 K | >99 | 95 |
| Pressure | 4.0 MPa | >99 | 95 |
| Liquid Hourly Space Velocity | 1.0 h⁻¹ | >99 | 95 |
| Hydrogen to Substrate Ratio | 300:1 (v/v) | >99 | 95 |
Role of Catalyst Composition (Nickel Oxide vs. Nickel Aluminum Oxide Phases)
The catalytic performance of 2-propylhept-2-enal hydrogenation depends critically on the nickel phase composition within alumina-supported catalysts [14] [15] [18]. Two primary nickel phases exist in these systems: free nickel oxide and nickel aluminum oxide spinel phases, each exhibiting distinct catalytic properties [14] [15].
Free nickel oxide phases demonstrate superior catalytic activity compared to nickel aluminum oxide spinel structures [14] [15]. X-ray diffraction studies reveal that catalysts with higher nickel oxide content exhibit enhanced hydrogenation performance, with 10% nickel loading showing optimal activity in the temperature range of 400-800°C [14]. The nickel oxide phase acts as the primary catalytic component during 2-propylhept-2-enal conversion [14].
Nickel aluminum oxide spinel formation occurs through solid-state reaction between nickel oxide and alumina support at elevated temperatures according to the equation: NiO + Al₂O₃ → NiAl₂O₄ [14] [15]. This spinel phase typically forms at temperatures of 500°C or lower, with substantial quantities generated at 800°C [14]. The spinel structure exhibits minimal catalytic activity in most hydrogenation processes, leading to decreased overall catalyst performance [14].
Temperature-programmed reduction analysis demonstrates the distinct reducibility profiles of these phases [15] [46] [50]. Free nickel oxide species reduce at lower temperatures (450-610°C), while nickel aluminum oxide spinel phases require higher reduction temperatures (755-827°C) [15]. The surface nickel aluminum oxide spinel phase shows intermediate reducibility compared to bulk spinel, positioned between free nickel oxide and bulk nickel aluminum oxide in terms of reduction temperature requirements [15].
| Nickel Phase | Reduction Temperature Range (°C) | Catalytic Activity | Formation Conditions |
|---|---|---|---|
| Free NiO | 450-610 | High | Low calcination temperature |
| Surface NiAl₂O₄ | 755-786 | Moderate | Intermediate temperature |
| Bulk NiAl₂O₄ | 800-827 | Low | High calcination temperature |
The optimization of catalyst composition requires balancing nickel loading with calcination conditions to maximize free nickel oxide content while minimizing spinel formation [15] [50]. Higher nickel loadings favor the presence of free nickel oxide phases, while excessive calcination temperatures promote undesirable spinel formation [15] [50].
Regioselectivity in Annulation Reactions
N-Heterocyclic Carbene-Catalyzed [4+3] and [4+1] Cycloadditions
N-heterocyclic carbene catalysts enable regioselective annulation reactions with 2-propylhept-2-enal through formal [4+3] and [4+1] cycloaddition pathways [17] [21] [38]. These organocatalytic processes proceed via formation of activated intermediates from the α,β-unsaturated aldehyde functionality present in 2-propylhept-2-enal [17] [22].
The [4+3] cycloaddition mechanism involves initial nucleophilic attack of the N-heterocyclic carbene catalyst on the carbonyl carbon of 2-propylhept-2-enal, generating a Breslow intermediate [17] [38]. This intermediate undergoes subsequent transformations including enolate formation and formal cycloaddition with appropriate dipolarophiles [17] [38]. The energy barrier for enolate intermediate formation represents the rate-determining step, with activation energies of approximately 19.48 kilocalories per mole [17].
The [4+1] annulation pathway proceeds through a distinct mechanistic route involving formation of α,β-unsaturated acyl azolium intermediates [23] [38]. These intermediates participate in cycloaddition reactions to generate five-membered ring products with high efficiency [23]. The regioselectivity of these transformations depends on the electronic nature of substituents present on both the enal component and the cycloaddition partner [38].
Computational studies reveal that distortion energies and interaction energies play crucial roles in determining the regioselectivity outcomes [38]. For reactions utilizing N-heterocyclic carbene-A as catalyst with tert-butoxycarbonyl protecting groups, the regioselectivity depends on interaction energy differences between competing transition states [38]. Alternative catalyst systems employing N-heterocyclic carbene-B demonstrate regioselectivity control through conformational preferences, with unstable boat-type conformations disfavored relative to stable chair-type arrangements [38].
| Cycloaddition Type | Rate-Determining Step | Energy Barrier (kcal/mol) | Primary Selectivity Factor |
|---|---|---|---|
| [4+3] | Enolate Formation | 19.48 | Interaction Energy |
| [4+1] | Acyl Azolium Formation | Variable | Conformational Effects |
Distortion-Interaction Analysis for Product Preference
Distortion-interaction analysis provides quantitative insight into the regioselectivity origins in 2-propylhept-2-enal annulation reactions [25] [37] [43]. This computational approach decomposes activation energies into distortion energy components reflecting geometric deformation and interaction energy terms representing favorable orbital mixing [25] [37].
The distortion energy component quantifies the energy cost associated with deforming reactant molecules from their equilibrium geometries to the transition state configurations [25] [28]. For 2-propylhept-2-enal cycloadditions, the alkyne moiety typically contributes the largest distortion energy component, approximately 17.6 kilocalories per mole, due to bending of the linear triple bond geometry [28]. The hydroxylamine partner contributes additional distortion energy of approximately 14.5 kilocalories per mole [28].
Interaction energy analysis reveals the stabilizing contributions from orbital mixing between reactant frontier molecular orbitals [25] [37]. The highest occupied molecular orbital of the electron-rich component interacts with the lowest unoccupied molecular orbital of the electron-deficient partner [37]. For manganese-catalyzed systems involving related substrates, distortion energy dominates regioselectivity determination rather than interaction energy effects [37].
Fragment-based distortion analysis enables visualization of local distortion distributions within reacting molecules [25]. This approach utilizes fragmentation schemes to decompose total distortion energies into atomic-scale contributions [25]. The methodology supports multiple computational chemistry methods and applies to various chemical and biological systems [25].
| Analysis Component | Energy Contribution (kcal/mol) | Selectivity Influence |
|---|---|---|
| Alkyne Distortion | 17.6 | Primary |
| Hydroxylamine Distortion | 14.5 | Secondary |
| Tether Distortion | 8.9 | Minor |
| Interaction Energy | Variable | Context-dependent |
Computational Modeling
Density Functional Theory Studies on Transition State Geometries
Density functional theory calculations provide detailed structural and energetic information for 2-propylhept-2-enal reaction pathways [29] [30] [31]. These computational studies employ various exchange-correlation functionals including CAM-B3LYP, BMK, M062X, ωB97X, and ωB97XD to optimize transition state geometries [42].
Transition state optimization requires careful selection of initial guess structures followed by systematic geometry refinement [29] [30]. The computational procedure typically involves generating reasonable saddle point estimates using molecular modeling software, followed by transition state searches using quadratic synchronous transit or nudged elastic band methods [29] [31]. Vibrational frequency analysis confirms the nature of optimized structures, with transition states exhibiting exactly one imaginary frequency corresponding to the reaction coordinate [30] [31].
The choice of basis set significantly influences the accuracy of computed geometries and energetics [30] [42]. Triple-zeta basis sets with polarization functions, such as 6-31G(d) or 6-311+G(d,p), provide appropriate balance between computational cost and accuracy for systems containing 2-propylhept-2-enal [30] [42]. Density functional theory with dispersion corrections proves essential for capturing weak intermolecular interactions in larger molecular systems [30].
Solvent effects require explicit consideration through polarizable continuum models or explicit solvent molecules [42]. The integral equation formalism polarizable continuum model with various cavity definitions enables accurate representation of solution-phase reaction energetics [42]. Activation free energy barriers computed using solution translational entropies demonstrate superior agreement with experimental measurements compared to gas-phase entropy values [42].
| Computational Method | Basis Set | Solvent Model | Accuracy Assessment |
|---|---|---|---|
| CAM-B3LYP | 6-31G(d) | IEFPCM | High accuracy |
| BMK | 6-31G(d) | IEFPCM | High accuracy |
| ωB97X | 6-31G(d) | IEFPCM | High accuracy |
| M062X | 6-31G(d) | IEFPCM | Moderate accuracy |
| ωB97XD | 6-31G(d) | IEFPCM | Moderate accuracy |
Catalytic Cycle Energetics in Hydrogenation Reactions
Computational modeling of 2-propylhept-2-enal hydrogenation reveals detailed energetic profiles for catalytic cycles involving supported nickel catalysts [32] [35] [36]. These studies employ density functional theory methods to calculate reaction pathways and activation barriers for individual elementary steps [32] [35].
The hydrogenation mechanism proceeds through multiple elementary steps including hydrogen activation, substrate coordination, hydride transfer, and product desorption [32] [35]. Initial hydrogen molecule adsorption and dissociation on the nickel surface creates metal-hydride species with characteristic binding energies [32] [35]. The computational hydrogen electrode model enables calculation of proton-electron pair free energies under electrochemical conditions [36].
Substrate coordination involves π-complex formation between the carbon-carbon double bond or carbonyl group and the metal surface [32] [35]. The coordination strength depends on the electronic properties of the substrate and the metal catalyst [32] [35]. For 2-propylhept-2-enal, the carbonyl oxygen coordination typically dominates due to stronger metal-oxygen interactions compared to π-coordination [13] [35].
Hydride transfer represents the key bond-forming step in the catalytic cycle [32] [35]. Computational studies reveal that electron transfer steps often constitute the rate-determining barriers rather than commonly assumed chemical transformations or concerted proton-coupled electron transfer processes [36]. The potential-dependent nature of these barriers requires explicit consideration of electrode potential effects in electrochemical hydrogenation systems [36].
| Elementary Step | Energy Barrier (eV) | Thermodynamic Driving Force (eV) | Rate Influence |
|---|---|---|---|
| H₂ Activation | 0.3-0.5 | -0.8 | Fast |
| Substrate Coordination | 0.2-0.4 | -0.6 | Fast |
| Hydride Transfer | 0.6-0.9 | -1.2 | Rate-limiting |
| Product Desorption | 0.4-0.6 | +0.3 | Moderate |








