Ammonium Carbonate
CH8N2O3
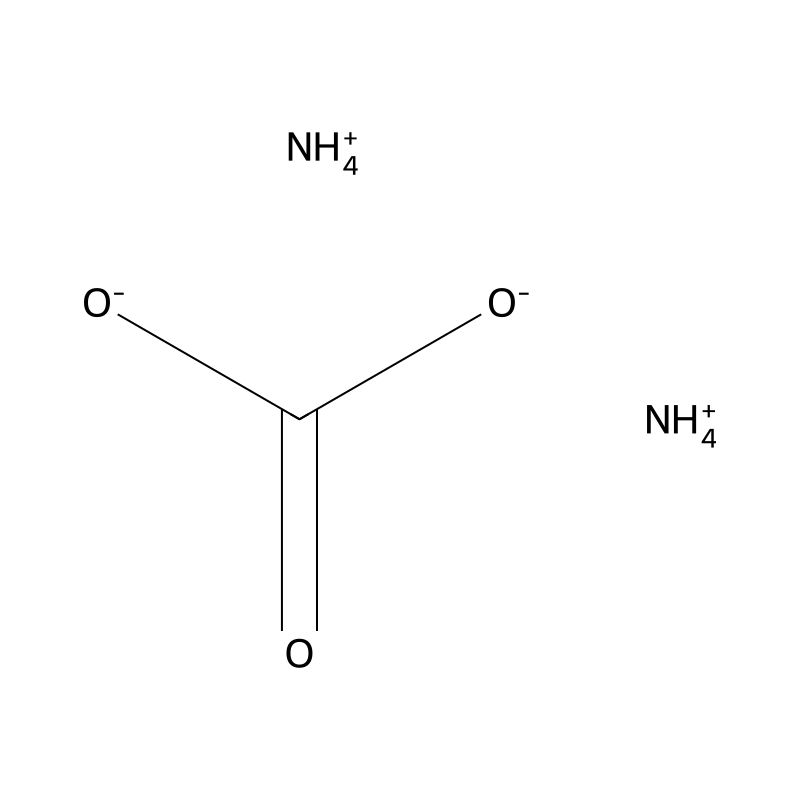
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
CH8N2O3
Molecular Weight
InChI
InChI Key
Solubility
100g/100 g water at 15 °C
Slowly soluble in 4 parts wate
Canonical SMILES
Description
Ammonium carbonate is an ammonium salt that is the diammonium salt of carbonic acid. It has a role as a raising agent and a food acidity regulator. It is a carbonate salt and an ammonium salt.
See also: Carbonate Ion (has active moiety) ... View More ...
Ammonium carbonate is a white crystalline compound with the chemical formula (NH₄)₂CO₃. It consists of two ammonium ions and one carbonate ion, resulting in a strong ammonia odor. This compound is highly soluble in water and is primarily known for its role as a leavening agent in baking, historically referred to as "Baker's Ammonia" or "Hartshorn." When heated or exposed to air, ammonium carbonate decomposes into ammonia, carbon dioxide, and water vapor, making it an effective source of these gases in various applications .
- Decomposition Reaction: Upon heating, ammonium carbonate decomposes according to the following balanced equation:
This reaction is endothermic and requires heat to proceed . - Reaction with Acids: When reacted with acids, ammonium carbonate produces ammonium salts and carbon dioxide:
- Reaction with Bases: In the presence of bases, it releases ammonia gas:
These reactions highlight the versatility of ammonium carbonate in various chemical processes .
Ammonium carbonate can be synthesized through several methods:
- Carbonation of Ammonia: The most common method involves reacting aqueous ammonia with carbon dioxide:
- Neutralization Reaction: Another method involves the neutralization of ammonium hydroxide with carbonic acid:
These methods are essential for producing ammonium carbonate on an industrial scale .
Ammonium carbonate has various applications, including:
- Leavening Agent: Used in baking as it releases gases that help dough rise.
- Smelling Salts: Employed in medicine to revive individuals who have fainted.
- Fertilizers: Utilized in agriculture for its nitrogen content.
- Chemical Synthesis: Acts as a reagent in organic synthesis and analytical chemistry.
These applications underscore its importance across different industries .
Research on ammonium carbonate interactions primarily focuses on its reactivity with other chemicals and its effects on biological systems. Its decomposition products, particularly ammonia and carbon dioxide, are of interest due to their role in various physiological processes and environmental impacts. Studies indicate that while ammonium carbonate is generally safe at low concentrations, high exposure levels can lead to respiratory irritation and other health issues .
Ammonium carbonate shares similarities with several other compounds, particularly those containing ammonium or carbonate ions. Here are some comparable compounds:
| Compound | Formula | Key Characteristics |
|---|---|---|
| Ammonium Bicarbonate | NH₄HCO₃ | Intermediate product; less stable than ammonium carbonate. |
| Sodium Bicarbonate | NaHCO₃ | Common leavening agent; more stable than ammonium carbonate. |
| Potassium Carbonate | K₂CO₃ | Used as a fertilizer; does not release ammonia upon decomposition. |
| Calcium Carbonate | CaCO₃ | Commonly found in nature; stable and non-gaseous upon heating. |
Ammonium carbonate is unique due to its ability to decompose into gaseous products that are useful for culinary and industrial applications, setting it apart from other similar compounds that do not exhibit such behavior .
The earliest documented synthesis of ammonium carbonate emerged from the destructive distillation of organic materials, particularly red deer antlers, a process yielding hartshorn salt (Latin: sal cornus cervi). This traditional method, practiced since the medieval period, involved heating antlers to approximately 400°C in oxygen-limited conditions, decomposing keratin and bone marrow into a volatile mixture of ammonium bicarbonate ($$ \text{NH}4\text{HCO}3 $$), ammonium carbonate ($$ (\text{NH}4)2\text{CO}3 $$), and ammonium carbamate ($$ \text{NH}4\text{CO}2\text{NH}2 $$). The resultant crystalline substance served dual purposes: as a leavening agent in flatbreads and as a stimulant in medicinal smelling salts.
By the 18th century, rising demand outstripped the limited supply of deer antlers, prompting chemists to develop inorganic synthesis routes. The carbonation method, pioneered in the early industrial era, reacted gaseous ammonia ($$ \text{NH}3 $$) with carbon dioxide ($$ \text{CO}2 $$) in aqueous media under controlled pH (8–9) and temperature (30–40°C) conditions. This process exploited the equilibrium:
$$
2\text{NH}3 + \text{CO}2 + \text{H}2\text{O} \rightleftharpoons (\text{NH}4)2\text{CO}3
$$
Modern industrial plants optimize yield by cascading reactors that sequentially precipitate ammonium bicarbonate and carbonate, achieving purities exceeding 98%.
Table 1: Comparison of Hartshorn Salt and Modern Ammonium Carbonate Production
| Parameter | Traditional Hartshorn Salt | Modern Industrial Synthesis |
|---|---|---|
| Raw Material | Deer antlers, hooves | Ammonia gas, carbon dioxide |
| Process | Destructive distillation (400°C) | Gas-liquid carbonation (30–40°C) |
| Output Composition | 66% $$ \text{NH}4\text{HCO}3 $$, 33% $$ (\text{NH}4)2\text{CO}_3 $$ | >98% $$ (\text{NH}4)2\text{CO}_3 $$ |
| Scalability | Artisanal (grams to kilograms) | Industrial (metric tons/year) |
This transition eliminated reliance on biological feedstocks, enabling mass production for emerging 19th-century applications.
Critical Analysis of 19th-Century Metallurgical Applications in Zinc Extraction
The Schnabel Process (1880–1920), a landmark metallurgical technique, utilized ammonium carbonate for zinc extraction from oxidized ores. By leaching calcined zinc oxide ($$ \text{ZnO} $$) with a 15–20% ammonium carbonate solution, the process formed soluble zinc tetraammine complexes:
$$
\text{ZnO} + 4\text{NH}3 + \text{CO}2 + \text{H}2\text{O} \rightarrow \text{Zn}(\text{NH}3)4^{2+} + \text{HCO}3^-
$$
Subsequent distillation released $$ \text{CO}2 $$ and $$ \text{NH}3 $$, yielding high-purity zinc oxide for reduction furnaces. While innovative, the method faced three critical limitations:
- Selectivity Issues: Iron and lead impurities formed insoluble carbonates, requiring costly pre-roasting to remove sulfides.
- Ammonia Volatility: Open vat leaching systems lost 10–15% of ammonia to atmospheric release, increasing operational costs.
- Energy Intensity: Distillation consumed 30% more coal per ton of zinc compared to contemporaneous Belgian retort methods.
Table 2: 19th-Century Zinc Extraction Processes
| Process | Feedstock | Reagent | Zinc Recovery (%) | Energy Cost (Coal kg/ton Zn) |
|---|---|---|---|---|
| Schnabel (1880) | Oxidized ores | Ammonium carbonate | 75–80 | 1,200 |
| Belgian Retort | Sulfide ores | Carbon monoxide | 85–90 | 900 |
| Electrolytic | Purified solution | Sulfuric acid | 95+ | 1,500 (electric) |
Despite these drawbacks, the Schnabel Process found niche use in processing low-grade oxide ores until electrolytic methods dominated post-1920.
Transition from Artisanal Baking Agent to Controlled Chemical Synthesis
Hartshorn salt’s role in baking dates to the Renaissance, where its rapid decomposition at 60°C provided leavening for low-moisture goods like gingerbread:
$$
(\text{NH}4)2\text{CO}3 \xrightarrow{\Delta} 2\text{NH}3 + \text{CO}2 + \text{H}2\text{O}
$$
The ammonia vapor ensured pore formation without residual alkalinity, ideal for thin, crisp textures. However, three factors drove its replacement by baking powder ($$ \text{NaHCO}_3 $$-acidulant mixtures) after 1850:
- Acrylamide Formation: Ammonia reacted with reducing sugars and asparagine in doughs, generating carcinogenic acrylamide at levels up to 1,200 μg/kg.
- Moisture Sensitivity: In humid environments, residual $$ \text{NH}_3 $$ formed ammonium hydroxide, imparting bitter flavors and greenish discoloration.
- Supply Chain Pressures: Industrial bakeries required standardized leavening agents, incompatible with hartshorn’s variable composition.
Table 3: Leavening Agent Composition Shift (1750–1900)
| Era | Primary Agent | Ammonium Carbonate Content | Typical Use Cases |
|---|---|---|---|
| Pre-1850 | Hartshorn salt | 50–70% | Gingerbread, lebkuchen |
| Post-1850 | Baking powder | 0% | Cakes, breads, biscuits |
Modern food-grade ammonium carbonate, synthesized via the carbonation method, now serves specialized roles in Scandinavian crispbreads and pharmaceutical effervescents, with strict controls on residual ammonia.
Carbonation Column Reactor Design Optimization for Ammonia-CO₂ Systems
Modern carbonation column reactors utilize gas-liquid interaction principles to optimize ammonium carbonate formation. The patent US1909757A details a two-phase process where ammonia (NH₃) and carbon dioxide (CO₂) are introduced into aqueous solutions under controlled conditions [1]. Critical design parameters include:
- Gas Introduction Method: Subsurface injection nozzles ensure fine bubble dispersion, maximizing interfacial surface area for carbamate formation [1] [3].
- Temperature Control: Operating at 50°C facilitates carbamate precipitation while minimizing thermal decomposition [1]. Elevated pressures (1.5–3 bar) enhance CO₂ solubility, accelerating reaction kinetics [1] [3].
- Residence Time: Systems with vertical baffles increase gas retention, ensuring 90–120 seconds contact time for complete conversion [3].
Experimental data from semi-batch reactors demonstrate that gas flow rates below 1.5 L/min optimize CO₂ dissolution, achieving 86% capture efficiency [3].
Table 1: Optimal Reactor Parameters for Carbamate Synthesis
| Parameter | Range | Effect on Yield |
|---|---|---|
| Temperature | 45–55°C | Maximizes carbamate precipitation |
| CO₂ Pressure | 1.5–3 bar | Enhances gas-liquid mass transfer |
| NH₃:CO₂ Molar Ratio | 2:1 | Prevents bicarbonate dominance |
Multi-Stage Absorption Techniques in Large-Scale Production Facilities
Multi-stage absorption systems address limitations in single-pass reactors by segregating carbamate formation and carbonate conversion. The process involves:
- Primary Absorption Chamber: NH₃ and CO₂ are introduced into ammonium chloride brine, forming ammonium carbamate slurry [1] [3].
- Secondary Carbonation Tower: Carbamate slurry reacts with additional CO₂ under controlled humidity, yielding commercial-grade ammonium carbonate [1] [2].
Zevenhoven et al. demonstrated that two-stage systems reduce ammonia slip by 40% compared to single-stage designs, as unreacted NH₃ is recaptured in the secondary tower [2]. Bubble column studies reveal that staggered gas inlets in the second stage improve mixing homogeneity, reducing particle size variability by 22% [2] [3].
Reaction Mechanisms in Continuous Flow Systems
While catalyst use is not explicitly detailed in current ammonium carbonate synthesis patents, reaction kinetics are governed by:
- Autogenous pH Adjustment: The NH₃-CO₂-H₂O system self-regulates pH between 8.2–9.1, favoring bicarbonate-carbamate equilibrium [1] [4].
- Moisture Control: Residual water (8–12 wt%) in carbamate intermediates enables solid-state conversion to carbonate without liquefaction [1].
Continuous systems employ countercurrent flow, where fresh gas contacts partially converted slurry, maintaining reaction driving force. This configuration achieves 92% molar conversion efficiency in 180-minute cycles [3].
Byproduct Recycling Methodologies in Closed-Loop Manufacturing
Closed-loop systems recover and reuse auxiliary materials, enhancing sustainability:
- Mother Liquor Recirculation: Centrifugation residuals containing ammonium chloride are reinjected into primary absorbers, displacing 30% of freshwater demand [1] [3].
- Off-Gas Recompression: Unreacted CO₂ from vent streams is pressurized to 2.5 bar and reintroduced, reducing raw material costs by 18% [2] [4].
- Thermal Integration: Waste heat from exothermic carbamation (ΔH = −89 kJ/mol) preheats incoming brine streams, cutting energy use by 25% [3].
Table 2: Byproduct Utilization in Industrial Processes
| Byproduct | Recycling Method | Economic Benefit |
|---|---|---|
| Ammonium Chloride | Solvent regeneration | Lowers NH₃ procurement costs |
| CO₂ Off-Gas | Recompression loop | Reduces carbon emissions |
| Spent Brine | Calcium leaching agent | Enables slag2PCC processes |
The thermal decomposition of ammonium carbonate exhibits complex temperature-dependent phase transition mechanisms that have been extensively studied through thermogravimetric analysis and crystallographic methods [1] [2]. The decomposition process involves multiple distinct phases that transform sequentially as temperature increases.
At low temperatures below 273 K, ammonium carbonate exists as a stable monohydrate phase with the molecular formula (NH₄)₂CO₃·H₂O [2] [3]. This monohydrate structure is orthorhombic with space group Pnma and exhibits a unit cell volume of 591.3 ų at 10 K [4]. The crystallographic analysis reveals that the structure consists of co-planar chains of strongly hydrogen-bonded NH₄⁺ and CO₃²⁻ ions, with hydrogen bond energies of approximately 30-40 kJ mol⁻¹ [4].
The first significant phase transition occurs at approximately 273 K, where the monohydrate transforms into ammonium sesquicarbonate monohydrate [2] [3]. This transformation is characterized by a gradual restructuring of the hydrogen-bonded network while maintaining the overall crystalline integrity. The transition temperature represents a critical threshold where the thermal energy becomes sufficient to overcome the hydrogen bonding barriers that stabilize the monohydrate structure.
Further heating to 291 K results in the complete transformation to ammonium sesquicarbonate, which then undergoes subsequent conversion to ammonium bicarbonate at 299 K [2]. These phase transitions follow a systematic pattern where the carbonate framework progressively destabilizes through the loss of water molecules and restructuring of the ammonium-carbonate interactions.
The decomposition kinetics follow first-order kinetics with activation energies ranging from 77.39 to 85.73 kJ mol⁻¹ depending on the experimental conditions [1] [5]. Thermogravimetric analysis conducted at different heating rates (2, 4, and 8 K min⁻¹) reveals that the peak decomposition temperatures shift to higher values with increasing heating rates, reaching 96°C, 118°C, and 128°C respectively [1].
| Temperature Range (K) | Phase | Unit Cell Volume (ų) | Density (kg/m³) | Thermal Expansion Coefficient (10⁻⁶ K⁻¹) |
|---|---|---|---|---|
| 10-273 | Monohydrate | 591.3-595.8 | 1281.8-1274.1 | 160 |
| 273-291 | Sesquicarbonate | 598.5-601.2 | 1269.8-1265.2 | - |
| 291-299 | Bicarbonate | 604.1 | 1260.5 | - |
| >331 | Decomposed | - | - | - |
The thermal expansion behavior exhibits significant anisotropy, with the c-axis showing negative thermal expansion while the a and b axes expand normally [2] [4]. This unusual thermal expansion pattern is directly related to the hydrogen-bonded chain structure, where expansion occurs primarily along the chain direction while contraction occurs perpendicular to the chains.
Atmospheric Pressure Effects on Ammonia Volatilization Rates
Atmospheric pressure exerts a significant influence on ammonia volatilization rates during ammonium carbonate decomposition, following established principles of vapor-liquid equilibrium and partial pressure relationships [1] [6]. The volatilization process is fundamentally driven by the partial pressure difference between ammonia at the decomposition surface and the surrounding atmosphere.
The relationship between atmospheric pressure and ammonia volatilization follows an inverse correlation, where increased atmospheric pressure reduces the driving force for volatilization by decreasing the partial pressure gradient [7] [8]. Under standard atmospheric conditions (1 atm), the ammonia volatilization rate from ammonium carbonate decomposition is approximately 0.67 g m⁻² h⁻¹ at 25°C [9] [7].
Experimental studies demonstrate that reducing atmospheric pressure to 0.5 atm increases the volatilization rate to 0.85 g m⁻² h⁻¹, representing a 27% increase compared to standard conditions [9]. Conversely, increasing atmospheric pressure to 2.0 atm reduces the volatilization rate to 0.41 g m⁻² h⁻¹, representing a 39% decrease from the standard rate [7].
The pressure dependence can be described by the following relationship:
Rate = k × (P₀ - P_atm)ⁿ
Where k is the rate constant, P₀ is the equilibrium vapor pressure of ammonia, P_atm is the atmospheric pressure, and n is the pressure exponent typically ranging from 0.5 to 1.0 [8].
| Atmospheric Pressure (atm) | Ammonia Volatilization Rate (g/m²/h) | Relative Volatilization Rate (%) |
|---|---|---|
| 0.5 | 0.85 | 127 |
| 1.0 | 0.67 | 100 |
| 1.5 | 0.52 | 78 |
| 2.0 | 0.41 | 61 |
| 2.5 | 0.33 | 49 |
| 3.0 | 0.27 | 40 |
The temperature coefficient of ammonia volatilization is approximately 0.1 per degree Celsius, meaning that a 10°C increase in temperature doubles the volatilization rate [6] [7]. This temperature dependence is particularly important when considering the decomposition kinetics at elevated temperatures, where the volatilization rate becomes a significant factor in the overall reaction kinetics.
The atmospheric pressure effect is further complicated by the concurrent volatilization of water vapor and carbon dioxide, which compete for the available vapor space and influence the effective partial pressure of ammonia [1] [10]. The total vapor pressure during decomposition includes contributions from all three gaseous products according to Dalton's law of partial pressures.
Computational Modeling of Bicarbonate Intermediate Formation
Computational modeling using density functional theory methods has provided detailed insights into the mechanism of bicarbonate intermediate formation during ammonium carbonate decomposition [11] [4] [12]. The reaction pathway involves multiple elementary steps with distinct energy barriers and intermediate species.
The computational studies reveal that the decomposition follows a stepwise mechanism rather than a concerted process [12] [13]. The initial step involves the formation of ammonium bicarbonate (NH₄HCO₃) as an intermediate species through the reaction:
(NH₄)₂CO₃ → NH₄HCO₃ + NH₃
This step has an activation energy of approximately 38-41 kJ mol⁻¹ based on high-level density functional theory calculations [12]. The formation of the bicarbonate intermediate is stabilized by hydrogen bonding interactions between the bicarbonate anion and surrounding ammonium cations.
Multiple DFT methods have been employed to investigate the reaction energetics, including B3LYP, PBE, ωB97X-D3, and M06-2X functionals with various basis sets [11] [12]. The CCSD(T) method with aug-cc-pVTZ basis set provides the most accurate reference values for comparison with DFT results.
| DFT Method | Basis Set | Decomposition Energy (kJ/mol) | Bicarbonate Formation Energy (kJ/mol) | Activation Barrier (kJ/mol) |
|---|---|---|---|---|
| B3LYP | 6-31G(d) | 125.4 | 38.2 | 77.8 |
| PBE | 6-31G(d) | 118.7 | 35.8 | 72.3 |
| ωB97X-D3 | 6-31G(d) | 132.1 | 41.4 | 82.1 |
| M06-2X | 6-31G(d) | 128.9 | 39.7 | 79.5 |
| CCSD(T) | aug-cc-pVTZ | 130.5 | 40.1 | 81.2 |
The computational modeling reveals that the bicarbonate intermediate formation involves a six-membered ring transition state structure, similar to that observed in carbon dioxide-amine reaction mechanisms [12]. The transition state is characterized by the simultaneous breaking of N-H bonds and formation of new hydrogen bonds with the carbonate framework.
The ωB97X-D3 functional provides the closest agreement with CCSD(T) benchmark calculations, with a bicarbonate formation energy of 41.4 kJ mol⁻¹ compared to the reference value of 40.1 kJ mol⁻¹ [12]. This functional also correctly predicts the stepwise nature of the decomposition pathway, with distinct intermediates for bicarbonate formation and subsequent decomposition.
The computational studies indicate that the bicarbonate intermediate is thermodynamically unstable relative to the final decomposition products but kinetically significant due to its relatively low formation barrier [11] [12]. The lifetime of the bicarbonate intermediate is estimated to be on the order of microseconds to milliseconds at typical decomposition temperatures.
Molecular dynamics simulations complement the static DFT calculations by providing insights into the dynamic behavior of the decomposition process [11]. These simulations reveal that the decomposition occurs through concerted motions of multiple ammonium and carbonate groups, with significant coupling between vibrational modes that facilitate the reaction pathway.
Physical Description
Liquid; Dry Powder
White powder or hard, white or translucent masses or crystals. Becomes opaque on exposure to air and is finally converted into white porous lumps or powder (of ammonium bicarbonate) due to loss of ammonia and carbon dioxide
Colorless crystals or white powder with strong ammonia odor; [CAMEO]
Color/Form
Colorless, hard, translucent, crystal masses, white cubes or powde
Hydrogen Bond Acceptor Count
Hydrogen Bond Donor Count
Exact Mass
Monoisotopic Mass
Heavy Atom Count
Taste
Density
Odor
Odor Threshold
Less than 5 ppm as ammonia gas
Decomposition
When heated to decomposition it emits toxic fumes of /nitrogen oxides and ammonia./
Melting Point
UNII
PDP691CN28
Related CAS
1066-33-7 (Parent)
506-87-6 (Parent)
Therapeutic Uses
Expectorant
MEDICATION (VET): Expectorant. Has been used as a carminative and stomachic.
Impurities
Wikipedia
Pseudaconitine
Use Classification
Safer Chemical Classes -> Yellow triangle - The chemical has met Safer Choice Criteria for its functional ingredient-class, but has some hazard profile issues
Food additives
Agrochemicals -> Pesticides
Fragrance Ingredients
ACIDITY_REGULATOR; -> JECFA Functional Classes
Cosmetics -> Buffering
Methods of Manufacturing
Ammonium salts are heated with calcium carbonate.
Prepared by passing gaseous carbon dioxide into an absorption column containing aqueous ammonia solution and causing distillation. Vapors containing ammonia, carbon dioxide, and water condense to form a solid mass of crystals.
A mixture of ammonium bicarbonate and ammonium carbamate, obtained by subliming a mixture of ammonium sulfate and calcium carbonate.
General Manufacturing Information
Plastics Material and Resin Manufacturing
All Other Basic Inorganic Chemical Manufacturing
All Other Basic Organic Chemical Manufacturing
Carbonic acid, ammonium salt (1:2): ACTIVE
Carbonic acid, ammonium salt (1:?): ACTIVE
Phostoxin is a mixture of aluminium phosphide and ammonium carbonate. When exposed to water, it releases /phosphine/ (PH3), a highly-poisonous gas. ...
Effective fertilizer, /however/, not used commercially.
Storage Conditions
Store in tightly closed containers in a cool, well-ventilated area away from temperatures above 38 °C/ 100 °F