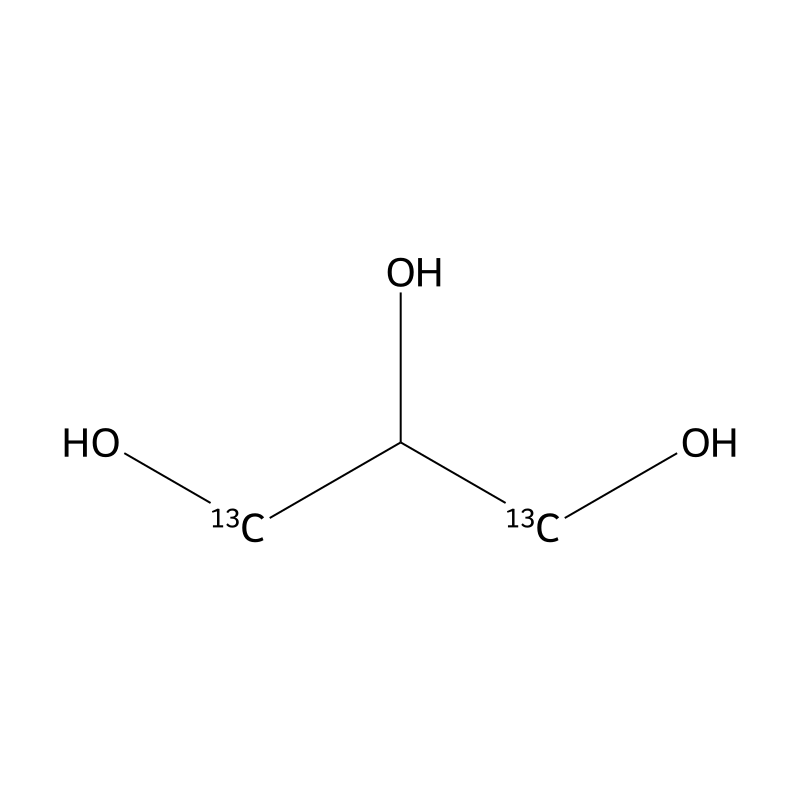
Glycerol-13C2

Glycerol-1,3-13C2 (CAS 102088-01-7) is a highly specialized stable isotope-labeled carbon source, typically supplied at ≥99 atom % 13C isotopic purity. As a selectively labeled trihydroxy alcohol, it features 13C atoms exclusively at the C1 and C3 positions, separated by an unlabeled 12C atom at the C2 position. This specific molecular architecture breaks the continuous carbon spin network, eliminating one-bond 13C-13C scalar and dipolar couplings that are inherent to uniformly labeled analogs. In procurement contexts, it is primarily sourced as a targeted metabolic precursor for the expression of sparsely labeled recombinant proteins in solid-state NMR (ssNMR) structural biology, a highly specific tracer for metabolic flux analysis (MFA), and a precision internal standard for isotope-dilution mass spectrometry (ID-MS) [1].

Substituting Glycerol-1,3-13C2 with uniformly labeled Glycerol-13C3 or unlabeled glycerol critically compromises advanced analytical workflows. In solid-state NMR structural biology, using U-13C3 glycerol results in uniformly labeled proteins where strong one-bond 13C-13C dipolar couplings cause 'dipolar truncation,' obscuring the weak, long-range inter-residue distance restraints necessary for 3D structure determination [1]. Conversely, the 1,3-13C2 labeling pattern yields a 'checkerboard' sparse labeling in expressed proteins, preserving these critical long-range signals. In mass spectrometry, substituting with deuterated analogs (e.g., Glycerol-d8) can introduce chromatographic isotope effects—shifting liquid chromatography retention times away from the endogenous analyte—whereas 13C-labeled glycerol strictly co-elutes, ensuring accurate absolute quantification [2].

Dipolar Truncation Suppression in ssNMR

When used as the sole carbon source in E. coli expression media, Glycerol-1,3-13C2 produces a 'checkerboard' sparse labeling pattern in recombinant proteins. This specific labeling eliminates adjacent 13C-13C pairs, thereby suppressing dipolar truncation. Studies on protein assemblies (such as viral capsids and SH3 domains) demonstrate that sparse labeling with 1,3-13C2 glycerol yields high-resolution 2D 13C-13C NMR spectra with individual signal line widths below 1 ppm, allowing the extraction of hundreds of long-range inter-residue distance restraints (e.g., over 280 restraints in SH3). In contrast, uniformly labeled proteins grown on U-13C3 glycerol produce highly congested spectra where strong one-bond couplings mask these critical long-range conformational signals [1].

Procurement of 1,3-13C2 glycerol is essential for structural biologists who need to determine the 3D structures of large, insoluble protein assemblies where uniform labeling fails.

Isotopomer Resolution in MFA

In metabolic engineering and fluxomics, Glycerol-1,3-13C2 is utilized to trace specific carbon cleavage and recombination events. Because the C2 position is unlabeled, downstream metabolites exhibit isolated 13C-1H spin systems without the interference of 13C-13C scalar couplings. For example, feeding 1,3-13C2 glycerol to microbial cultures yields distinct C10/C20,C40-13C2-labeled ribose moieties, providing clear, quantifiable NMR and MS signals for specific pathway fluxes. Uniformly labeled U-13C3 glycerol, by contrast, generates fully labeled metabolites where extensive scalar couplings complicate multiplet patterns, increasing the standard deviation of calculated metabolic fluxes and obscuring specific carbon-bond cleavage events [1].

Allows metabolic engineers to accurately quantify competing intracellular fluxes that cannot be mathematically resolved using uniformly labeled substrates.

Co-Eluting Internal Standard for ID-MS

Glycerol-1,3-13C2 serves as a reliable internal standard for the absolute quantification of free glycerol in human serum and urine via isotope-dilution mass spectrometry (ID-MS). It provides a precise +2 Da mass shift (m/z +2) compared to endogenous glycerol, avoiding overlap with natural M+0 and M+1 isotopes. Unlike deuterated standards (e.g., Glycerol-d8), which can exhibit a chromatographic isotope effect leading to retention time shifts in LC-MS, Glycerol-1,3-13C2 strictly co-elutes with the unlabeled target analyte. This ensures identical ionization suppression or enhancement effects, yielding analytical recoveries averaging approximately 90% and strictly linear calibration curves (1.0–1000 µg/mL) without the need for complex sample pre-concentration [1].

Crucial for clinical and analytical laboratories procuring internal standards that require perfect matrix-effect matching for validated diagnostic assays.

ssNMR of Protein Assemblies

Glycerol-1,3-13C2 is procured as a carbon source for expressing recombinant proteins (such as viral capsids, amyloid fibrils, and membrane proteins) destined for Magic-Angle Spinning (MAS) solid-state NMR. Its sparse labeling pattern suppresses dipolar truncation, allowing researchers to measure the long-range inter-residue distances required to solve complex 3D macromolecular structures [1].

Metabolic Flux Analysis (MFA)

In industrial biotechnology and metabolic engineering, this compound is selected to map intracellular carbon fluxes. By feeding microbial or mammalian cells with 1,3-13C2 glycerol, researchers can track the specific cleavage and recombination of carbon backbones through central carbon metabolism, distinguishing between pathways (like glycolysis versus pentose phosphate) that would be indistinguishable with uniformly labeled substrates [2].

Clinical ID-MS

Procured by clinical diagnostic labs and reference material manufacturers, Glycerol-1,3-13C2 acts as a quantitative internal standard for measuring free glycerol and triglycerides in serum or urine. Its 13C-based mass shift ensures strict chromatographic co-elution with endogenous analytes, avoiding the isotope effects common with deuterated standards and ensuring absolute quantitative accuracy [3].