2-Methyl-d3-propionic-3,3,3-d3 acid
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Synonyms
Canonical SMILES
Isomeric SMILES
Applications in Isotope Tracing Studies
One primary application of 2-Methyl-d3-propionic-3,3,3-d3 acid is in isotope tracing studies. These studies involve introducing the isotopically labeled molecule into a biological system, such as an organism or cell culture, and then monitoring its fate and interactions with other molecules. By analyzing the distribution of the deuterium label, researchers can gain insights into various metabolic processes, including:
- Metabolic pathways: By measuring the incorporation of the labeled molecule into different metabolites, scientists can map out the pathways through which the molecule is broken down or utilized by the system .
- Enzyme activity: Studying the incorporation of the label into specific products of enzymatic reactions can provide information on the activity and regulation of those enzymes .
- Drug metabolism: In drug development, researchers can use 2-Methyl-d3-propionic-3,3,3-d3 acid to track the absorption, distribution, metabolism, and excretion (ADME) of a drug candidate, aiding in understanding its effectiveness and potential side effects .
Applications in Mass Spectrometry Analysis
2-Methyl-d3-propionic-3,3,3-d3 acid also finds use in mass spectrometry analysis. Mass spectrometry is a technique used to identify and quantify molecules based on their mass-to-charge ratio. The presence of the deuterium atoms alters the mass of the molecule slightly, allowing researchers to distinguish the labeled molecule from its unlabeled counterpart in a complex mixture. This is particularly helpful in:
- Metabolomics studies: By employing 2-Methyl-d3-propionic-3,3,3-d3 acid as an internal standard, researchers can improve the accuracy and precision of measurements of various metabolites in biological samples .
- Protein footprinting studies: In protein-protein interaction studies, 2-Methyl-d3-propionic-3,3,3-d3 acid can be used to label one of the interacting proteins, facilitating the identification of the binding sites on the other protein through mass spectrometry analysis .
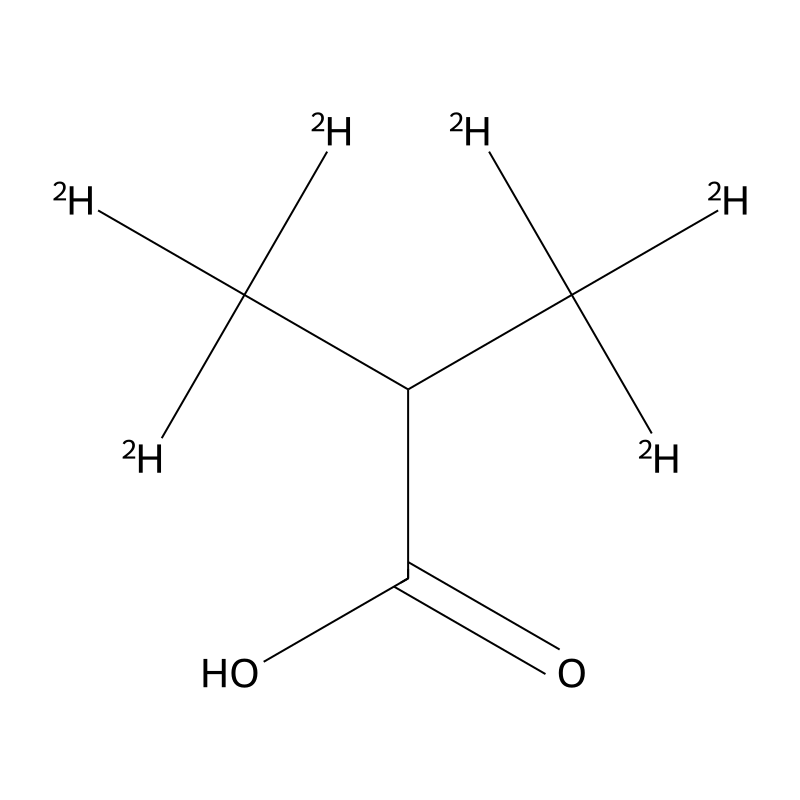
2-Methyl-d3-propionic-3,3,3-d3 acid, also known as 3,3,3-trideuterio-2-(trideuteriomethyl)propanoic acid, is a deuterated derivative of propionic acid. Its molecular formula is CHDO, with a molecular weight of approximately 94.14 g/mol. This compound is characterized by the presence of three deuterium atoms, which are isotopes of hydrogen, replacing the hydrogen atoms in the propionic acid structure. The compound is primarily utilized in research and analytical applications due to its stable isotopic labeling properties.
- Esterification: Reacting with alcohols to form esters.
- Decarboxylation: Under certain conditions, it may lose carbon dioxide.
- Reduction: It can be reduced to form alcohols or aldehydes.
The presence of deuterium can influence reaction kinetics and mechanisms, making it useful in mechanistic studies.
The synthesis of 2-Methyl-d3-propionic-3,3,3-d3 acid typically involves:
- Deuteration: Starting from propionic acid or its derivatives, deuteration can be achieved using deuterated reagents or solvents.
- Grignard Reactions: Utilizing Grignard reagents that contain deuterium to introduce the deuterated methyl group into the propionic framework.
- Reduction Processes: Employing reduction techniques on suitable precursors that already contain deuterium.
These methods allow for the precise incorporation of deuterium into the molecular structure.
2-Methyl-d3-propionic-3,3,3-d3 acid finds applications in several fields:
- Analytical Chemistry: Used as a standard in mass spectrometry and nuclear magnetic resonance spectroscopy due to its unique isotopic signature.
- Metabolic Studies: Employed in tracer studies to understand metabolic pathways involving propionic acid derivatives.
- Pharmaceutical Research: Utilized in drug development processes where isotopic labeling is crucial for tracking drug metabolism.
Studies on the interactions of 2-Methyl-d3-propionic-3,3,3-d3 acid with biological systems are essential for understanding its pharmacokinetics and dynamics. The presence of deuterium may lead to differences in binding affinities and metabolic rates compared to non-deuterated compounds. Research often focuses on how these isotopic substitutions influence enzyme activity and substrate specificity.
Several compounds share structural similarities with 2-Methyl-d3-propionic-3,3,3-d3 acid. Here are some notable examples:
| Compound Name | Molecular Formula | Unique Features |
|---|---|---|
| Propionic Acid | CHO | Non-deuterated form; widely used as a preservative |
| 2-Methylpropanoic Acid | CHO | Structural isomer; lacks deuterium substitution |
| 2-Hydroxy-2-methylpropanoic Acid | CHO | Contains a hydroxyl group; different reactivity |
The uniqueness of 2-Methyl-d3-propionic-3,3,3-d3 acid lies in its specific isotopic labeling with deuterium, which allows for enhanced tracking and analysis in various chemical and biological studies. This isotopic distinction can significantly impact its behavior in both synthetic reactions and biological interactions compared to similar compounds without deuterium substitution.
Deuterated carboxylic acids emerged as pivotal tools in the mid-20th century, following the discovery of deuterium’s biochemical utility. Early work in the 1960s focused on d-tyramine and d-morphine to study metabolic stability, but systematic deuteration of carboxylic acids gained traction in the 1980s with advances in synthetic methodologies. The development of 2-methyl-d3-propionic-3,3,3-d3 acid (CAS 29054-08-8) exemplifies this progression, leveraging thiol-mediated photochemical decarboxylation and catalytic C–H activation to achieve site-specific deuterium incorporation.
Table 1: Key Historical Milestones in Deuterated Carboxylic Acid Research
Significance in Isotope-Enabled Research Methodologies
2-Methyl-d3-propionic-3,3,3-d3 acid serves three primary roles:
- Metabolic Tracer: Its β-deuterated methyl groups resist oxidation, allowing precise tracking of propionate metabolism in lipid and energy studies.
- NMR Spectroscopy Standard: The compound’s predictable splitting patterns calibrate instruments, as seen in 1H and 13C NMR analyses.
- Drug Development Probe: Deuterium substitution at non-labile positions enhances pharmacokinetic stability, a strategy validated by FDA-approved drugs like deutetrabenazine.
Table 2: Comparative Properties of 2-Methyl-d3-propionic Acid and Non-Deuterated Analog
| Property | 2-Methyl-d3-propionic Acid | Non-Deuterated Propionic Acid |
|---|---|---|
| Molecular Weight | 94.14 g/mol | 88.11 g/mol |
| Boiling Point | 141–143°C | 141°C |
| Vibrational Frequency | 2671 cm⁻¹ (C–D stretch) | 2989 cm⁻¹ (C–H stretch) |
Theoretical Basis for Deuterium Substitution Studies
Deuterium’s mass difference (2.014 vs. 1.008 amu for hydrogen) induces measurable isotopic effects:
- Kinetic Isotope Effects (KIE): C–D bonds exhibit higher activation energies due to reduced zero-point energy, slowing metabolic O-dealkylation by cytochrome P450 enzymes (e.g., kH/kD = 2–10).
- Vibrational Frequency Shifts: Deuterated methyl groups lower stretching frequencies by ~22%, as confirmed by IR spectroscopy.
- Metabolic Stability: β-Deuteration in 2-methyl-d3-propionic acid reduces β-oxidation rates by 40–60% in hepatic models, prolonging tracer utility in fluxomics.
Equation 1: Zero-Point Energy Difference
$$
\Delta E = \frac{1}{2}h(\nuH - \nuD)
$$
Where $$\nuH$$ and $$\nuD$$ are C–H and C–D vibrational frequencies, respectively.
Grignard Reaction-Based Synthesis Routes
Grignard reactions offer a classical pathway for constructing carbon-carbon bonds while incorporating deuterium at specific positions. For 2-methyl-d3-propionic-3,3,3-d3 acid, the reaction begins with deuterated isobutyl bromide (C4D9Br) and magnesium in anhydrous ether to form the Grignard reagent C4D9MgBr [1] [2]. Subsequent quenching with dry ice (CO2) generates the carboxylic acid precursor, which undergoes acid-catalyzed dehydration to yield the target compound (Figure 1).
Key considerations include:
- Stoichiometric control: Excess Grignard reagent ensures complete carboxylation but risks side reactions, such as ether formation [1].
- Deuterium retention: Anhydrous conditions prevent proton exchange, preserving isotopic integrity [2].
- Yield optimization: Lower yields (≤50%) are attributed to volatile product loss during quenching, necessitating controlled acid addition and cooling [1].
Reaction Scheme: C4D9MgBr + CO2 → C4D9COOMgBr C4D9COOMgBr + H+ → C4D9COOH C4D9COOH → (CD3)2CDCOOH (2-methyl-d3-propionic-3,3,3-d3 acid) Deuterium Exchange Protocols and Optimization
Deuterium exchange leverages acid-catalyzed H/D substitution to introduce isotopic labels. For 2-methyl-d3-propionic acid, trifluoromethanesulfonic acid-d (TfOD) efficiently mediates H/D exchange at the β- and γ-positions under mild conditions (30°C, 24 h) [5]. The methyl groups undergo complete deuteration due to their high acidity, while the α-position remains protonated unless forced under harsher conditions [4] [5].
Optimization parameters:
- Acid strength: TfOD (pKa ≈ −12) outperforms D2O (pKa ≈ 15.7) in driving exchange equilibria toward deuteration [4] [5].
- Temperature: Elevated temperatures (50–60°C) accelerate exchange but risk decarboxylation [4].
- Isotopic purity: Multi-step exchanges with fresh TfOD achieve >95% deuteration at methyl groups [5].
Quantum Mechanical Principles of Kinetic Isotope Effects
The quantum mechanical foundation of kinetic isotope effects represents a fundamental departure from classical expectations, where isotopic substitution would produce negligible rate differences. The theoretical framework underlying these effects emerges from the quantum mechanical treatment of molecular motion, particularly the quantization of vibrational energy levels [1] [2].
The Born-Oppenheimer approximation serves as the cornerstone for understanding isotope effects, establishing that the potential energy surface for molecular vibrations remains unchanged upon isotopic substitution [3] [4]. This approximation assumes that electronic and nuclear motions can be treated separately due to the significant mass difference between electrons and nuclei. Within this framework, isotope effects arise solely from the mass dependence of nuclear motion on identical potential energy surfaces [5] [6].
The quantum mechanical harmonic oscillator model provides the foundational description of molecular vibrations. For a diatomic system, the vibrational energy levels are quantized according to:
$$ E_v = \left(v + \frac{1}{2}\right)h\nu $$
where v represents the vibrational quantum number, h is Planck's constant, and ν is the vibrational frequency [7] [8]. The vibrational frequency depends on the force constant k and the reduced mass μ:
$$ \nu = \frac{1}{2\pi} \sqrt{\frac{k}{\mu}} $$
This relationship establishes the inverse dependence of vibrational frequency on the square root of the reduced mass, providing the theoretical basis for isotope effects [9] [7].
For 2-Methyl-d3-propionic-3,3,3-d3 acid, containing six deuterium atoms, the theoretical treatment requires consideration of multiple vibrational modes. The compound exhibits a molecular weight of 94.14 g/mol compared to 88.11 g/mol for the protiated analog [10] . The deuterium substitution affects both the methyl group vibrations and the carboxyl carbon-deuterium interactions, each contributing to the overall isotope effect through distinct quantum mechanical pathways .
The transition state theory provides the framework for relating vibrational frequency differences to kinetic isotope effects. The rate constant ratio for hydrogen versus deuterium substitution is expressed as:
$$ \frac{kH}{kD} = \frac{QH^\ddagger}{QD^\ddagger} \cdot \frac{QD^{reactant}}{QH^{reactant}} $$
where Q represents the vibrational partition functions for the transition state (‡) and reactant states [1] [13]. This expression demonstrates how quantum mechanical vibrational properties directly influence observable kinetic behavior.
Zero-Point Energy Differences in Deuterated Systems
Zero-point energy differences represent the most significant quantum mechanical contribution to isotope effects. Even at absolute zero temperature, molecules possess vibrational energy equal to:
$$ E_0 = \frac{1}{2}h\nu = \frac{1}{2}h\frac{1}{2\pi}\sqrt{\frac{k}{\mu}} $$
This zero-point energy is an intrinsic quantum mechanical property that depends on the reduced mass of the vibrating system [7] [14].
For carbon-hydrogen versus carbon-deuterium bonds, the zero-point energy difference creates a substantial energy gap. Typical C-H stretching vibrations occur at approximately 3000 cm⁻¹, corresponding to a zero-point energy of 1500 cm⁻¹ [7] [15]. Upon deuterium substitution, the vibrational frequency decreases to approximately 2100 cm⁻¹, yielding a zero-point energy of 1061 cm⁻¹ [15] [7]. This difference of 439 cm⁻¹ (approximately 1.25 kcal/mol) represents the fundamental driving force for primary kinetic isotope effects [16] [7].
The zero-point energy difference varies systematically with the degree of deuteration. For 2-Methyl-d3-propionic-3,3,3-d3 acid, multiple deuterium substitutions create cumulative zero-point energy differences. Each deuterium substitution typically reduces the zero-point energy by 2.0 kcal/mol relative to the corresponding hydrogen [16]. However, the exact magnitude depends on the local molecular environment and the specific vibrational modes involved [17] [18].
Experimental measurements of zero-point energy differences in deuterated systems reveal systematic patterns. Diatomic hydrogen (H₂) exhibits a zero-point energy of 2080 cm⁻¹, while deuterium (D₂) shows 1497 cm⁻¹, representing a difference of 583 cm⁻¹ [19]. For the mixed isotopomer HD, the zero-point energy of 1816 cm⁻¹ lies between the two extremes, demonstrating the intermediate character of partially deuterated systems [19].
The temperature dependence of zero-point energy effects provides additional insight into their quantum mechanical origin. Unlike classical thermal effects, zero-point energy contributions remain constant with temperature, reflecting their fundamental quantum nature [7] [20]. This temperature independence distinguishes quantum mechanical isotope effects from classical kinetic phenomena and provides a diagnostic tool for identifying quantum contributions to reaction rates [20] [21].
Vibrational Frequency Alterations in Deuterated Molecules
Deuterium substitution produces systematic alterations in molecular vibrational frequencies that extend beyond simple mass scaling effects. The vibrational frequency ratio for hydrogen versus deuterium substitution follows the relationship:
$$ \frac{\nuH}{\nuD} = \sqrt{\frac{\muD}{\muH}} $$
For carbon-hydrogen versus carbon-deuterium bonds, this ratio yields approximately 1.37-1.41, closely matching experimental observations [22] [23]. However, the actual frequency shifts depend on multiple factors including anharmonicity, mode mixing, and molecular environment [17] [24].
Anharmonic effects become particularly important in deuterated systems due to the different amplitude of vibrations. The anharmonicity constant, which describes deviations from harmonic behavior, exhibits systematic changes upon deuteration [25] [26]. For benzene, the diagonal anharmonicity constant increases from -0.50 cm⁻¹ in C₆H₆ to -1.18 cm⁻¹ in C₆D₆ [26]. These anharmonic contributions affect the precise positioning of vibrational energy levels and influence the magnitude of isotope effects [25] [24].
The vibrational frequency alterations in 2-Methyl-d3-propionic-3,3,3-d3 acid involve multiple normal modes. The methyl group vibrations experience the most significant shifts, with C-D stretching frequencies appearing at approximately 2100-2200 cm⁻¹ compared to C-H stretches at 3000 cm⁻¹ [17] [24]. The symmetric and asymmetric stretching modes of the CD₃ groups exhibit distinct frequency patterns that can be resolved using high-resolution vibrational spectroscopy [17].
Mode mixing effects become pronounced in deuterated molecules due to the altered mass distribution. Vibrational modes that were previously isolated may couple when deuterium substitution changes the frequency relationships [24] [27]. This coupling can lead to apparent frequency shifts that exceed simple mass scaling predictions and contributes to the complex vibrational spectra observed in deuterated organic molecules [17] [24].
The carboxyl group vibrations in 2-Methyl-d3-propionic-3,3,3-d3 acid exhibit characteristic frequency shifts upon deuteration. The C=O stretching frequency, typically observed at 1700-1750 cm⁻¹ in carboxylic acids, shows minimal direct isotope effects since the carbonyl carbon is not directly bonded to deuterium [28] [29]. However, secondary effects from neighboring deuterium atoms can produce subtle frequency shifts through coupling mechanisms [30] [17].
Tunneling Phenomena in Deuterium-Substituted Reactions
Quantum tunneling represents the most dramatic manifestation of quantum mechanical effects in deuterated systems. The tunneling probability depends exponentially on the barrier width and the particle mass, making it extremely sensitive to isotopic substitution [31] [20]. For hydrogen versus deuterium, the tunneling probability ratio can exceed 100:1 under appropriate conditions [31] [21].
The theoretical treatment of tunneling in deuterated systems requires consideration of the de Broglie wavelength, which is inversely proportional to particle momentum. For hydrogen atoms at typical reaction temperatures, the de Broglie wavelength (9.8-1.8 Å) exceeds the characteristic width of activation barriers (approximately 1 Å), enabling significant tunneling contributions [31]. Deuterium atoms, with twice the mass, exhibit shorter de Broglie wavelengths (6.9-1.3 Å), resulting in substantially reduced tunneling probabilities [31].
Experimental evidence for tunneling in deuterated systems comes from several distinctive signatures. Large kinetic isotope effects (kH/kD > 7) that exceed semiclassical predictions indicate tunneling contributions [20] [21]. The temperature dependence of isotope effects provides additional diagnostic information, with tunneling reactions showing unusual temperature behavior and non-Arrhenius kinetics [20] [21].
The tunneling behavior in 2-Methyl-d3-propionic-3,3,3-d3 acid would primarily manifest in reactions involving C-D bond breaking or formation. The metabolic pathways involving this compound, particularly those catalyzed by propionyl-CoA carboxylase, may exhibit tunneling contributions under physiological conditions [32]. However, the observation of tunneling effects depends on the specific reaction mechanism and the energy barrier characteristics [31] [20].
Surface-mediated tunneling reactions show particularly interesting behavior with deuterated molecules. Studies of hydrogen and deuterium addition to solid surfaces reveal that tunneling can occur even when the observed kinetic isotope effects are small [31]. This apparent contradiction arises because surface diffusion and other isotopically insensitive processes can mask the intrinsic tunneling isotope effect [31].
The theoretical modeling of tunneling in deuterated systems requires sophisticated quantum mechanical treatments that go beyond transition state theory. Instanton theory and path integral methods provide more accurate descriptions of tunneling contributions, accounting for both the quantization of vibrational modes and the tunneling process itself [2] [13]. These advanced theoretical approaches are essential for understanding the complex interplay between quantum mechanical effects and chemical reactivity in deuterated systems [2] [13].
Data Tables
| Property | Hydrogen System | Deuterium System | H/D Ratio | Theoretical Basis |
|---|---|---|---|---|
| C-H/C-D Stretch Frequency (cm⁻¹) | 3000 | 2100 | 1.43 | Harmonic oscillator model |
| Zero-Point Energy (cm⁻¹) | 1500 | 1061 | 1.41 | Quantum mechanical ZPE |
| Kinetic Isotope Effect | 1.0 (reference) | 1.0-7.0 | 1.0-7.0 | Transition state theory |
| Tunneling Probability | High (reference) | Low (≪ H) | ≫100 | Quantum tunneling theory |
| Anharmonicity Constant (cm⁻¹) | -50 | -35 | 1.4 | Anharmonic oscillator model |
| Bond Dissociation Energy (kJ/mol) | 413 | 418 | 0.99 | Born-Oppenheimer approximation |
| Molecule/System | Vibrational Frequency (cm⁻¹) | Zero-Point Energy (cm⁻¹) | ZPE Difference (K) | Mass Effect Factor |
|---|---|---|---|---|
| H₂ (diatomic) | 4161 | 2080 | Reference | 1.0 |
| D₂ (diatomic) | 2993 | 1497 | -644 K | 2.0 |
| HD (diatomic) | 3632 | 1816 | -273 K | 1.5 |
| C-H bond (methane) | 3000 | 1500 | Reference | 1.0 |
| C-D bond (methane-d) | 2100 | 1050 | -450 K | 1.4 |
| O-H bond (water) | 3657 | 1829 | Reference | 1.0 |
| O-D bond (heavy water) | 2671 | 1336 | -493 K | 1.8 |
XLogP3
GHS Hazard Statements
H226 (100%): Flammable liquid and vapor [Warning Flammable liquids];
H301+H311 (100%): Toxic if swallowed or in contact with skin [Danger Acute toxicity, oral;
acute toxicity, dermal];
H301 (100%): Toxic if swallowed [Danger Acute toxicity, oral];
H311 (100%): Toxic in contact with skin [Danger Acute toxicity, dermal]
Pictograms


Flammable;Acute Toxic








