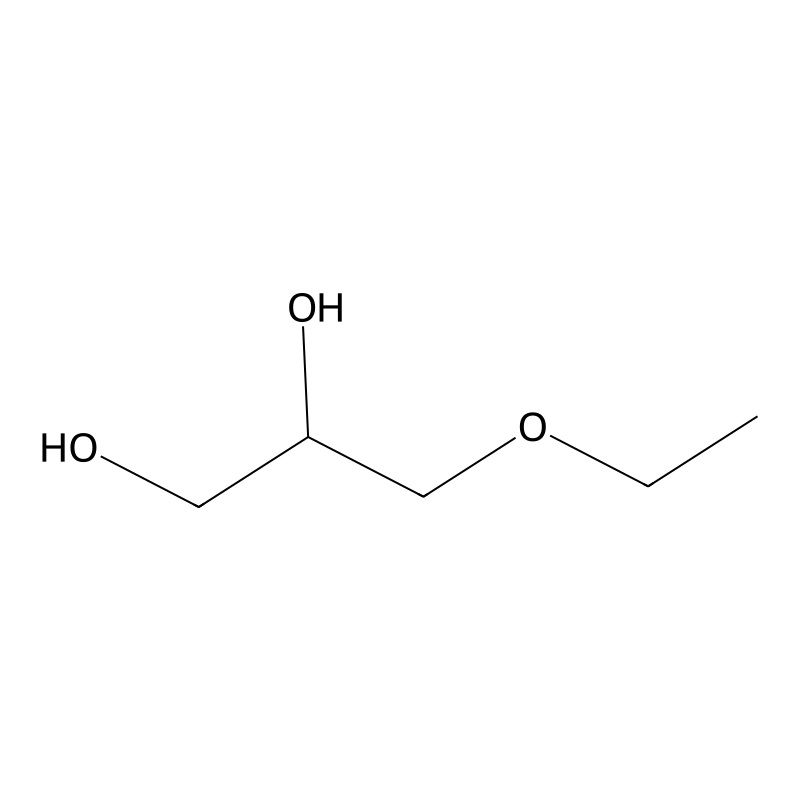
3-Ethoxy-1,2-propanediol

Solvent Applications:

-Ethoxy-1,2-propanediol (also known as glycerol α-ethyl ether) finds application in various scientific research fields due to its solvent properties. Its miscibility with both polar and non-polar compounds makes it a versatile tool for:

• Dissolving diverse molecules: It can dissolve various organic and inorganic compounds, making it useful in extraction procedures, sample preparation, and purification processes in various research areas like biochemistry, analytical chemistry, and material science [].
• Studying biological processes: Its ability to dissolve biological molecules like proteins, lipids, and carbohydrates makes it valuable for studying various biological processes in cell culture experiments and biomolecule characterization [].

Biomedical Applications:

Beyond its solvent properties, 3-Ethoxy-1,2-propanediol shows promise in specific areas of biomedical research:

• Development of hydrogels: It can act as a crosslinking agent in the formation of poly(glycidol) hydrogels, which are biocompatible materials with potential applications in tissue engineering and drug delivery systems []. These hydrogels can mimic the natural extracellular matrix, providing a supportive environment for cell growth and drug release in targeted tissues [].
• Glycosylation reactions: Studies suggest its potential as an acceptor substrate in glycosylation reactions catalyzed by the enzyme sucrose phosphorylase. This enzyme plays a crucial role in carbohydrate metabolism, and understanding its functions is essential in various fields, including biofuel production and development of therapeutic drugs targeting carbohydrate-based pathways [].

Other Research Applications:

• Analyte protection in gas chromatography: 3-Ethoxy-1,2-propanediol can be used as a derivatization agent in gas chromatography (GC) analysis of pesticides. This process helps protect the analytes from degradation during the analysis, improving the sensitivity and accuracy of the measurements [].

3-Ethoxy-1,2-propanediol, with the chemical formula C$_5$H$_{12}$O$_3$, is a colorless, odorless, and viscous liquid. It is classified as a glycerol ether and is characterized by its hygroscopic properties, making it capable of absorbing moisture from the environment. This compound is primarily used as a solvent in various applications, including pharmaceuticals and cosmetics . Its molecular weight is approximately 120.15 g/mol .

EGE is considered to have low to moderate toxicity []. However, proper handling is crucial to avoid potential hazards:

• Skin and eye irritant: EGE can irritate the skin and eyes upon contact [].
• Flammability: EGE is combustible and should be kept away from heat sources [].

• Esterification: It can react with carboxylic acids to form esters.
• Dehydration: Under certain conditions, it may lose water to form ethers or alkenes.
• Oxidation: The hydroxyl groups can be oxidized to form carbonyl compounds.

These reactions are essential for its use in synthesizing various derivatives and formulations .

Several methods exist for synthesizing 3-Ethoxy-1,2-propanediol:

• Etherification: This method involves the reaction of glycerol with ethyl iodide or ethylene oxide in the presence of a base.
• Transesterification: Glycerol can be reacted with ethyl acetate under acidic or basic conditions to yield 3-Ethoxy-1,2-propanediol.
• Direct Ethoxylation: Ethylene oxide can be reacted directly with glycerol at elevated temperatures and pressures.

These methods vary in efficiency and yield depending on the reaction conditions .

3-Ethoxy-1,2-propanediol finds diverse applications across several industries:

• Pharmaceuticals: Used as a solvent for drug formulations.
• Cosmetics: Acts as a humectant and solvent in skincare products.
• Food Industry: Occasionally utilized as a food additive for flavoring and preservation.
• Industrial