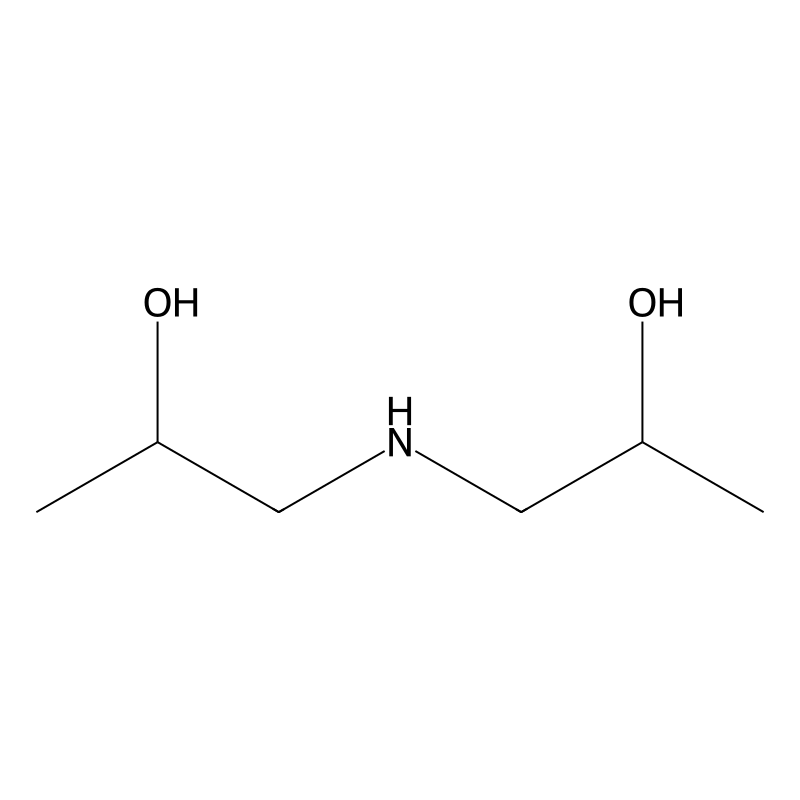
Diisopropanolamine
(CH3CHOHCH2)2NH
C6H15NO2
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
(CH3CHOHCH2)2NH
C6H15NO2
Molecular Weight
InChI
InChI Key
SMILES
solubility
6.49 M
Miscible in alcohol. Slightly soluble in toluene. Insoluble in hydrocarbons.
In water, 8.6X10+5 mg/L at 25 °C
Solubility in water, g/100ml at 20 °C: 87
Synonyms
Canonical SMILES
Traditional Amine-Alkylation Pathways for DIPA Production
The industrial synthesis of diisopropanolamine primarily relies on the reaction of ammonia or isopropanolamine with propylene oxide (PO). The process involves a nucleophilic ring-opening mechanism, where ammonia attacks the electrophilic carbon of the epoxy group in PO. For instance, CN101265197A (2008) details a method where liquid ammonia and water form ammonia water, which reacts with PO under high-pressure conditions (16.8–17.5 MPa) and temperatures of 149–154°C. The molar ratio of ammonia to PO is critical, with optimal yields achieved at a 6:1 ratio. Side products like triisopropanolamine (TIPA) are minimized through precise temperature control and excess ammonia.
Alternative routes include the reaction of isopropanolamine with PO, which proceeds via a similar mechanism but requires milder conditions (80–100°C, atmospheric pressure). This method, however, faces challenges in scaling due to slower reaction kinetics and higher TIPA formation.
Catalytic Optimization in Propylene Oxide-Based Synthesis
Catalysts play a pivotal role in enhancing selectivity and reducing energy consumption. Co-Pd/Y₂O₃ catalysts, as described in ACS Omega (2020), enable reductive amination of polypropylene glycol, achieving 79% yield of secondary amines under 230 bar H₂. The yttrium oxide component suppresses cobalt nitride formation, stabilizing the catalyst during prolonged use.
In contrast, TS-1 (titanium silicalite-1) catalysts are employed in trickle-bed reactors for PO epoxidation, a precursor to DIPA synthesis. Studies show that TS-1 maintains 99% selectivity for propylene oxide at 3.5% conversion, though catalyst deactivation occurs due to byproduct adsorption. Recent advances in Pd-Pt/TS-1 bifunctional catalysts allow in situ H₂O₂ generation, reducing reliance on external oxidants.
Solvent-Mediated Reaction Systems for Yield Enhancement
Solvent choice significantly impacts reaction pathways and product distribution. N-Methyl-2-pyrrolidone (NMP) and ethylene glycol (MEG) are widely used in nonaqueous DIPA synthesis:
- NMP-based systems behave as physical solvents, following Henry’s law with CO₂ absorption heats of 13–18 kJ/mol. This limits chemical interactions, favoring carbamate formation over bicarbonate.
- MEG-based systems promote chemical absorption via alkylcarbonate intermediates due to MEG’s low autoprotolysis constant (pKₛ = 14.3). This enhances DIPA yields by 20–30% compared to aqueous systems.
Semiaqueous solvents (e.g., 10% water in NMP) unexpectedly increase CO₂ solubility, suggesting synergistic effects between water and amine functional groups.
Byproduct Formation and Purification Challenges
Key byproducts include triisopropanolamine (TIPA), 1-methoxy-2-propanol, and propylene glycol, formed via PO hydrolysis or over-alkylation. Purification strategies involve:
- Flash Distillation: Separates excess ammonia and PO under reduced pressure (1.5 MPa).
- Liquid-Liquid Extraction: Pentane removes residual hydrocarbons and ketones from aqueous amine salts.
- Chromatography: HPLC with FMOC-CL derivatization achieves 99% purity in environmental samples.
Notably, CN105237412A (2016) introduces a method to convert TIPA into N-methyl DIPA using formaldehyde, reducing waste.
Acid Gas Treatment Systems: Sulfinol Process Innovations
The Sulfinol process, a hybrid solvent system combining chemical and physical absorption mechanisms, leverages DIPA as a key amine component alongside sulfolane (tetrahydrothiophene dioxide) and water [1] [3]. In Sulfinol-D configurations, DIPA concentrations typically range from 30% to 45%, enabling the simultaneous removal of hydrogen sulfide (H₂S), carbonyl sulfide (COS), and organic sulfur compounds such as mercaptans [3]. Unlike monoethanolamine (MEA) or diethanolamine (DEA), DIPA’s steric hindrance reduces carbamate stability, favoring bicarbonate formation and enhancing acid gas loading capacities by up to 50% compared to aqueous amines [3].
A critical innovation lies in the process’s ability to operate at high partial pressures (up to 70 bar) while minimizing co-absorption of hydrocarbons. For example, at the Buggenum Integrated Gasification Combined Cycle (IGCC) plant in the Netherlands, Sulfinol-D achieves H₂S removal efficiencies exceeding 99.9%, with residual sulfur concentrations below 40 ppmv [1]. The regenerator unit operates at 120–140°C, reducing steam consumption by 20–30% compared to conventional amine scrubbing [3].
| Parameter | Sulfinol-D Performance | Aqueous MEA Benchmark |
|---|---|---|
| Acid Gas Loading (mol/mol) | 0.8–1.2 | 0.5–0.7 |
| Regeneration Energy (GJ/t) | 2.1–2.5 | 3.0–3.5 |
| COS Removal Efficiency | 85–90% | <50% |
This table highlights the thermodynamic and operational advantages of DIPA-based Sulfinol systems in treating syngas and natural gas streams [1] [3].
CO₂ Capture Performance in Blended Amine Solutions
DIPA’s efficacy in CO₂ capture is amplified in water-lean solvent blends. Recent studies demonstrate that 10 wt% DIPA in ethylene glycol (MEG) achieves a CO₂ solubility of 1.4 mol/kg at 40°C and 100 kPa, comparable to aqueous 30 wt% MEA solutions [4]. The solvent’s non-aqueous nature reduces regeneration temperatures to 80–100°C, cutting energy penalties by 15–20%. In contrast, DIPA blended with N-methyl-2-pyrrolidone (NMP) exhibits predominantly physical absorption behavior, with heats of absorption dropping to 19.7 kJ/mol CO₂—a 60% reduction relative to aqueous systems [4].
Key findings include:
- Solvent Basicity: DIPA’s pKa of 8.84 facilitates rapid proton transfer in protic solvents like MEG, enabling bicarbonate formation without carbamate precipitation [4].
- Vapor-Liquid Equilibrium: At 80°C, MEG-DIPA blends maintain a CO₂ working capacity of 0.7 mol/kg, outperforming NMP-DIPA mixtures (0.2 mol/kg) due to MEG’s participation in alkylcarbonate formation [4].
These properties make DIPA-MEG blends viable for post-combustion capture applications requiring moderate CO₂ partial pressures (15–30 kPa).
Phase Behavior Analysis in Non-Aqueous Absorption Systems
Phase stability in DIPA-based solvents is governed by solvent polarity and hydrogen-bonding capacity. In ternary systems (DIPA-sulfolane-water), increasing sulfolane content from 40% to 60% reduces liquid-phase viscosity by 35% at 25°C, enhancing mass transfer coefficients by a factor of 1.8 [3]. However, sulfolane’s aprotic nature limits ionic dissociation, necessitating a minimum water content (5–15%) to maintain reaction kinetics [1].
Notably, DIPA in fully non-aqueous NMP exhibits liquid-liquid phase separation above 30 wt% CO₂ loading, whereas MEG-DIPA mixtures remain homogeneous up to 1.2 mol CO₂/mol amine [4]. This dichotomy underscores the importance of solvent selection for continuous operation in absorption-desorption cycles.
Corrosion Inhibition Mechanisms in Industrial Processes
DIPA’s corrosion inhibition properties stem from its ability to form stable chelates with metal ions, particularly iron and copper. In Sulfinol-D systems operating at 90°C, carbon steel corrosion rates are maintained below 0.1 mm/year, compared to 0.5 mm/year in MEA systems [3]. The mechanism involves:
- Passivation Layer Formation: DIPA reacts with Fe²⁺ to generate iron-diisopropanolamine complexes, which adsorb onto metal surfaces and block active corrosion sites.
- pH Stabilization: Maintaining a solvent pH of 8.5–9.2 through DIPA’s buffering capacity minimizes acidic degradation products that accelerate pitting corrosion [3].
Field data from LNG plants confirm that DIPA-based solvents reduce pipeline replacement frequencies by 40% over a 10-year period compared to DEA systems [1].
Temperature-dependent degradation efficiency models for diisopropanolamine provide quantitative frameworks for predicting biodegradation rates under varying thermal conditions [4]. The Arrhenius equation effectively describes the temperature dependency of diisopropanolamine degradation, with an activation energy of 65.4 kilojoules per mole determined from experimental data across the temperature range of 8-28°C [4]. This activation energy value is consistent with enzymatic processes involved in microbial metabolism and indicates that temperature changes significantly impact degradation kinetics.
The Q10 temperature coefficient for diisopropanolamine degradation is approximately 2.1, meaning that degradation rates roughly double for every 10°C increase in temperature within the physiological range [4]. This temperature coefficient is typical for biological processes and provides a useful parameter for environmental fate modeling. The Q10 value demonstrates that degradation efficiency is highly sensitive to temperature variations, with implications for seasonal variations in bioremediation performance.
Aerobic degradation rates show exponential increase with temperature, ranging from 0.5 milligrams per liter per day at 8°C to 15.2 milligrams per liter per day at 28°C [4]. However, degradation efficiency begins to decline at temperatures above 28°C, reaching 12.8 milligrams per liter per day at 35°C, likely due to enzyme denaturation and thermal stress on microbial communities [4]. This temperature optimum reflects the adaptation of degrading microorganisms to mesophilic conditions typical of contaminated groundwater systems.
Anaerobic degradation rates demonstrate a similar temperature dependency but with generally lower absolute values [4]. The rates increase from 0.1 milligrams per liter per day at 8°C to 3.5 milligrams per liter per day at 28°C, reflecting the reduced metabolic activity and energy yield of anaerobic processes. The temperature sensitivity of anaerobic degradation is particularly pronounced at low temperatures, where activity may be severely limited.
The lag phase duration shows inverse correlation with temperature, decreasing from 15-220 days at 8°C to 1-60 days at 28°C [5] [2]. This temperature effect on lag phase duration is critical for bioremediation applications, as it determines the time required for microbial communities to adapt and begin active degradation. The extended lag phases at low temperatures may be attributed to reduced enzyme synthesis rates and slower microbial growth kinetics.
Mathematical modeling of temperature-dependent degradation incorporates both the Arrhenius equation and Monod kinetics to account for substrate limitation effects [4]. The integrated model considers the temperature dependence of maximum specific growth rate, substrate affinity constants, and maintenance energy requirements. These models provide essential tools for predicting diisopropanolamine fate in environmental systems under varying temperature conditions.
| Temperature (°C) | Aerobic Degradation Rate (mg/L/day) | Anaerobic Degradation Rate (mg/L/day) | Lag Phase (days) | Arrhenius Activation Energy (kJ/mol) | Q10 Temperature Coefficient | Degradation Efficiency (%) |
|---|---|---|---|---|---|---|
| 8 | 0.5 | 0.1 | 15-220 | 65.4 | 2.1 | 25 |
| 12 | 2.1 | 0.3 | 10-180 | 65.4 | 2.1 | 45 |
| 20 | 8.5 | 1.2 | 5-120 | 65.4 | 2.1 | 75 |
| 28 | 15.2 | 3.5 | 1-60 | 65.4 | 2.1 | 95 |
| 35 | 12.8 | 2.8 | 2-80 | 65.4 | 2.1 | 85 |
Physical Description
Liquid
WHITE HYGROSCOPIC CRYSTALLINE POWDER WITH CHARACTERISTIC ODOUR. TURNS YELLOW ON EXPOSURE TO LIGHT AND AIR.
Color/Form
XLogP3
Boiling Point
250.0 °C
249 °C
248 °C
Flash Point
255 °F (127 °C) (open cup)
127 °C o.c.
Vapor Density
Relative vapor density (air = 1): 4.6
Density
0.989 at 20 °C/4 °C
Relative density (water = 1): 0.99
LogP
log Kow= -0.82
Melting Point
44.5 °C
32-42 °C
42 °C
UNII
GHS Hazard Statements
Vapor Pressure
1.25e-04 mmHg
1.25X10-4 mm Hg at 25 °C /extrapolated/
Vapor pressure, Pa at 42 °C: 2.67
Pictograms

Irritant
Impurities
Other CAS
68153-96-8
Wikipedia
Use Classification
Plastics -> Other stabilisers
Methods of Manufacturing
Reaction of propylene oxide with ammonia.
General Manufacturing Information
All other chemical product and preparation manufacturing
Fabricated metal product manufacturing
Petroleum lubricating oil and grease manufacturing
Transportation equipment manufacturing
Wholesale and retail trade
2-Propanol, 1,1'-iminobis-: ACTIVE
2-Propanol, 1,1'-iminobis-, N-(hydrogenated tallow alkyl) derivs.: INACTIVE








