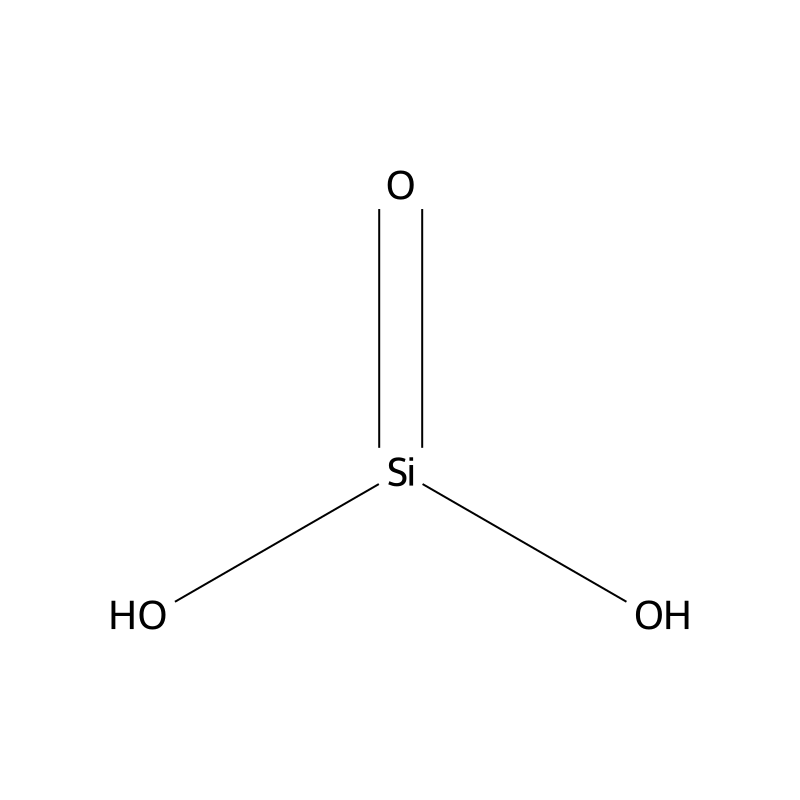
Metasilicic acid

Metasilicic acid (H2SiO3) is a partially hydrated, polymeric oxoacid of silicon that serves as a highly valuable intermediate between unstable monomeric orthosilicic acid and fully dehydrated silicon dioxide. Commercially procured as a high-purity colloidal gel or precipitated powder, it is characterized by its retained structural hydroxyl groups (SiO(OH)2) and its ability to form controlled three-dimensional siloxane networks [1]. In industrial procurement, it is primarily valued as an alkali-free precursor for advanced mesoporous silica and zeolites, a high-capacity adsorbent in chromatography, and a specialized flocculant in water treatment . Its controlled polymerization dynamics and elevated surface reactivity make it a superior choice for manufacturing applications that require precise structural templating, tunable porosity, or active heavy metal complexation.

Substituting metasilicic acid with common alternatives like sodium metasilicate or standard silica gel introduces severe processing liabilities and performance deficits. Sodium metasilicate, the most common industrial silica source, is highly alkaline and introduces unwanted sodium ions, which can disrupt the templating of mesoporous materials and poison the catalytic acidity of synthesized zeolites [1]. Conversely, fully dehydrated amorphous silica (SiO2) lacks the dense surface hydroxyl groups necessary for active chemical complexation, drastically reducing its efficacy as an adsorbent or flocculant[2]. Furthermore, orthosilicic acid is practically non-viable for industrial procurement due to its extreme instability and rapid, uncontrolled polymerization. Therefore, metasilicic acid is non-interchangeable when a process requires a high-purity, reactive, and easily templated silica precursor without alkali metal contamination.

Mesoporous Material and Zeolite Synthesis Yield

When used as a silica source for zeolite synthesis alongside templating agents like tetrapropylammonium hydroxide (TPAOH), metasilicic acid enables the formation of highly structured porous networks without the interference of sodium ions. Comparative synthesis models demonstrate that metasilicic acid yields zeolites with high specific surface areas (approx. 276 m²/g) and tunable SiO2/Al2O3 ratios (e.g., 18.4) [1]. In contrast, using sodium metasilicate requires rigorous downstream ion-exchange steps to remove residual sodium, which often results in lower structural purity and compromised catalytic acidity.

Allows catalyst and advanced material manufacturers to streamline synthesis workflows by eliminating costly and time-consuming ion-exchange purification steps.

Polymerization Control and Sol-Gel Processing Stability

The polymerization dynamics of silicic acids dictate their utility in sol-gel manufacturing. Orthosilicic acid (H4SiO4) is strictly monomeric and highly unstable, with monomeric solutions reacting completely within approximately 75 seconds at standard concentrations [1]. Metasilicic acid, possessing an ionization equilibrium constant (K1) of approximately 2 × 10^-10, exists in a partially condensed, colloidal state that offers a much wider and more predictable processing window [2]. This controlled reactivity allows formulators to precisely engineer the viscosity, porosity, and curing time of advanced materials.

Provides manufacturers of inorganic coatings and binders with the necessary working time and rheological control that is impossible to achieve with highly unstable monomeric precursors.

Surface Hydroxyl Density and Chemical Adsorption Capacity

Metasilicic acid (H2SiO3) maintains a higher concentration of active structural hydroxyl groups compared to fully calcined silica gel (SiO2) [1]. These hydroxyls act as primary binding sites for heavy metals, organic pollutants, and suspended particulates. While standard silica gel is largely inert and relies primarily on physical porosity, metasilicic acid undergoes active surface complexation and hydrogen bonding. This elevated chemical activity translates to superior flocculation performance in wastewater treatment and higher binding capacities in solid-phase extraction.

Essential for procurement in water treatment and analytical chemistry where maximizing the capture of trace contaminants or specific analytes is required.

Alkali-Free Precursor for Advanced Zeolites and Catalysts

Directly leverages metasilicic acid's ability to yield high surface area (276 m²/g) materials without introducing sodium ions [1]. It is the ideal precursor for synthesizing high-purity mesoporous silica and tunable zeolites where residual alkali metals would poison catalytic sites or disrupt structural templating.

Controlled Sol-Gel Binder for Advanced Coatings

Takes advantage of metasilicic acid's stable colloidal polymerization profile (K1 ≈ 2 × 10^-10) compared to highly unstable orthosilicic acid [2]. It allows formulators to create durable, high-performance inorganic coatings and adhesives with predictable curing times and rheology.

High-Capacity Flocculant for Industrial Wastewater Treatment

Utilizes the high density of surface hydroxyl groups to actively bind and coagulate heavy metals and suspended particulates . It is preferred over inert silica gels when active chemical complexation is required to meet strict environmental discharge limits.

Specialized Stationary Phases in Chromatography

Capitalizes on the retained hydroxyl activity to provide superior solid-phase extraction (SPE) and chromatographic separation capabilities for polar or complex biological macromolecules, outperforming standard dehydrated silica in specific analytical workflows.