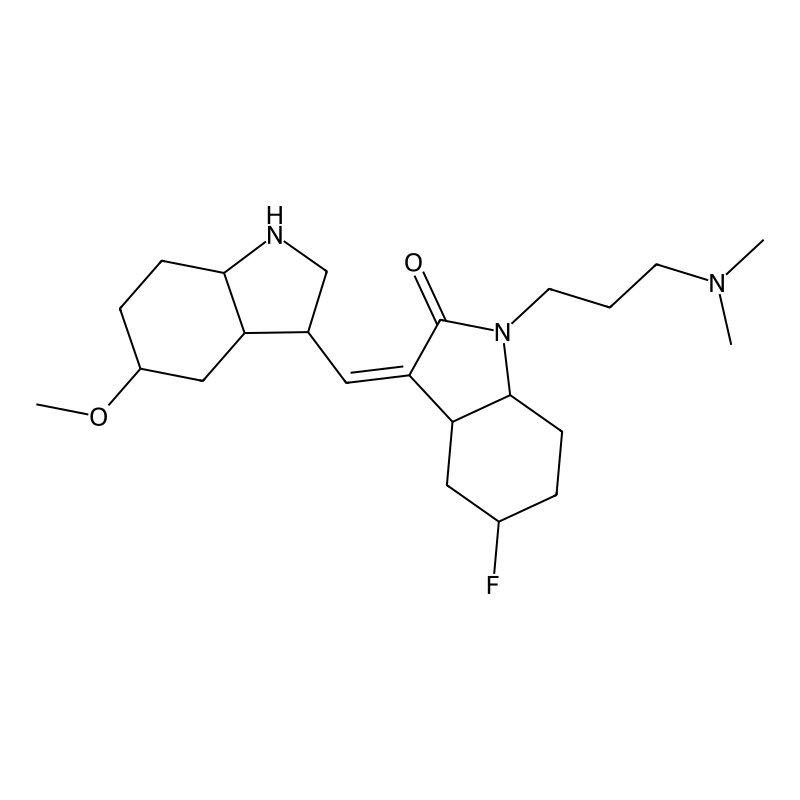
Terbium trifluoride

Luminescence and Lanthanide Chemistry:

• Upconversion: TbF₃ exhibits efficient upconversion properties, where it absorbs lower-energy photons and emits higher-energy ones. This phenomenon makes it a valuable material for developing anti-Stokes luminescent materials used in diverse applications like bioimaging, solar cells, and displays [].
• Solid-state lighting and displays: TbF₃ doped with other lanthanide ions like Eu³⁺ or Dy³⁺ exhibits strong luminescence, making it a potential candidate for solid-state lighting and displays. The specific dopant and its concentration determine the emitted color, enabling researchers to tailor the material for specific applications [].

Fluoride-based materials and catalysis:

• Fluoride-based glasses and ceramics: TbF₃ can be incorporated into fluoride-based glasses and ceramics, enhancing their properties like thermal stability, mechanical strength, and luminescent characteristics. These materials are being explored for applications in solid-state lasers, optical fibers, and biocompatible materials [].
• Catalysis: TbF₃ has been investigated as a potential catalyst for various chemical reactions, including dehydration and hydrogenation reactions. Its Lewis acidity and ability to bind to specific molecules make it a promising candidate for developing new and efficient catalytic systems [].

Nanotechnology and thin films:

• Nanoparticles: TbF₃ nanoparticles can be synthesized with controlled size and morphology, exhibiting unique optical and magnetic properties. These nanoparticles are being explored for applications in biolabeling, drug delivery, and magnetic resonance imaging contrast agents [].
• Thin films: TbF₃ thin films can be deposited on various substrates using techniques like sputtering or pulsed laser deposition. These films exhibit interesting electrical and optical properties, making them potential candidates for electronic devices, sensors, and optoelectronic applications [].

Other research applications:

• Solid-state lasers: TbF₃ doped with other lanthanide ions has been explored as a potential gain medium for solid-state lasers due to its efficient luminescent properties [].
• Biomedical applications: TbF₃ nanoparticles are being investigated for their potential use in bioimaging and drug delivery due to their unique optical properties and biocompatibility.

Origin and Significance:

Terbium trifluoride does not readily occur naturally but is synthesized in laboratories. One method involves reacting terbium(III) carbonate with hydrofluoric acid [1]. Terbium trifluoride plays a crucial role in the production of metallic terbium, a rare-earth element with applications in solid-state lasers, phosphors, and data storage devices [2].

(Citation 1)

Wikipedia - Terbium(III) fluoride (Citation 2): Ereztech - Terbium (III) Fluoride | Terbium trifluoride | TbF3

Molecular Structure Analysis

Key Features:

Terbium trifluoride adopts a hexagonal crystal structure with each terbium (Tb³⁺) cation surrounded by nine fluoride (F⁻) anions in a tricapped trigonal prismatic arrangement [3]. This structure allows for strong ionic bonding between the terbium and fluorine ions.

(Citation 3)

American Elements - Terbium Trifluoride

Notable Aspects:

The arrangement of F⁻ ions around Tb³⁺ creates a local environment with cubic symmetry. This symmetry is essential for certain applications, such as terbium-doped fluoride crystals used in solid-state lasers [4].

(Citation 4)

M. Gaft, et al. "Spectroscopic properties of trivalent terbium in KY3F10 crystals" (2001):

Chemical Reactions Analysis

Synthesis:

A common method for synthesizing TbF₃ involves reacting terbium(III) carbonate (Tb₂(CO₃)₃) with hydrofluoric acid (HF) at an elevated temperature:

Tb₂(CO₃)₃ + 6HF → 2TbF₃ + 3CO₂ + 3H₂O [1]

Reduction:

Terbium trifluoride can be reduced to metallic terbium using a strong reducing agent like calcium metal at high temperatures:

2 TbF₃ + 3 Ca → 3 CaF₂ + 2 Tb [2]

(Citation 1)

Same as section 1, Citation 1(Citation 2): Same as section 1, Citation 2

Other Relevant Reactions:

Due to its ionic nature, TbF₃ can react with other ionic compounds depending on the specific conditions. Research explores its interactions with various molten salts for potential applications in molten salt reactors [5].

(Citation 5)

N. Xu, et al. "Solubility of Rare Earth Fluorides in Molten NaF-KF-ZrF4" (2010):

Physical And Chemical Properties Analysis

• Melting Point: 1172 °C [1, 6]
• Boiling Point: 2280 °C [1, 6]
• Solubility: Insoluble in water [1, 6]
• Appearance: White powder [4, 6]
• Density: 7.2 g/cm³ [6]

(Citation 1)

Same as section 1, Citation 1(Citation 4): Same as section 2, Citation 4(Citation 6): ProChem, Inc. - Terbium (III) Fluoride