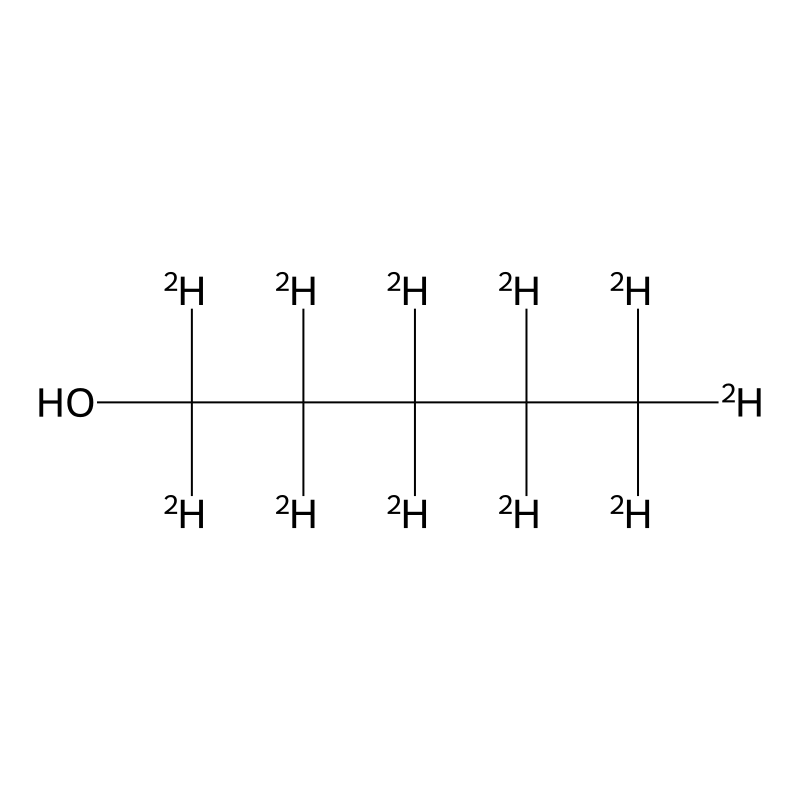
1-Pentan-d11-ol

1-Pentan-d11-ol (CAS 126840-22-0) is a fully deuterated primary aliphatic alcohol, formulated as CD3(CD2)4OH with an isotopic purity typically exceeding 98 atom % D . In industrial and analytical procurement, this compound serves primarily as a heavy-isotope internal standard for mass spectrometry, a contrast-matching solvent in small-angle neutron scattering (SANS), and a dynamically polarized target material in nuclear physics . The complete deuteration of the alkyl chain increases its molecular weight by 11 Da compared to its unlabeled counterpart, fundamentally altering its mass-to-charge ratio, coherent neutron scattering length, and magnetic spin properties without significantly changing its macroscopic chemical reactivity or fluid dynamics .

Procuring unlabeled 1-pentanol or partially deuterated analogs (e.g., 1-pentan-d3-ol) as substitutes for 1-pentan-d11-ol results in critical failures across specialized workflows. In mass spectrometry, unlabeled 1-pentanol exhibits complete spectral overlap with endogenous analytes, rendering it useless for isotope dilution and matrix effect normalization [1]. In structural biology and materials science, substituting the D11 form with unlabeled pentanol prevents the precise matching of scattering length densities (SLD) in D2O/H2O solvent mixtures, destroying the contrast required to isolate cosurfactant phases in SANS experiments [2]. Furthermore, in polarized target physics, hydrogenated materials fail to reach the >50% deuteron polarization thresholds achieved by the fully deuterated D11 form under 5.0 T magnetic fields, resulting in insufficient signal-to-noise ratios for neutron scattering.

Mass Shift for Absolute Quantification

In GC-MS and LC-MS workflows, 1-pentan-d11-ol provides a +11 Da mass shift compared to its unlabeled counterpart [1]. This shift bypasses the natural isotopic envelope (13C, 18O) of endogenous 1-pentanol and related volatile organic compounds. When used as an internal standard, it co-elutes chromatographically with the target analyte but is resolved in the m/z domain, ensuring normalization of matrix effects and extraction losses [1].

Procurement of the fully deuterated D11 form guarantees signal isolation, which is required for reproducible, regulatory-compliant quantitative assays.

SANS Contrast Matching for Phase Isolation

In SANS studies of surfactant-based systems, the structural role of the cosurfactant is determined by exchanging unlabeled 1-pentanol with 1-pentan-d11-ol [1]. Because deuterium has a coherent neutron scattering length (6.67 fm) different from hydrogen (-3.74 fm), the deuterated pentanol alters the scattering length density (SLD) of the micellar phase. By matching the SLD of the solvent, researchers can render specific phases invisible to neutrons, isolating the structural dimensions of the pentanol-rich domains [1].

Buyers in soft matter and materials science require the fully deuterated form to selectively resolve nanostructures in complex formulations.

Deuteron Polarization for Scattering Targets

Irradiated deuterated 1-pentanol is utilized as a dynamically polarized solid target in nuclear scattering experiments. Under high magnetic fields and cryogenic temperatures, it achieves targeted deuteron polarization[1]. Studies show that irradiated deuterated 1-pentanol reaches >50% deuteron polarization at 5.0 T, a performance metric that is higher than hydrogenated materials and comparable to benchmark deuterated butanol targets [1].

For physics facilities procuring target materials, the D11 form provides the signal-to-noise ratio required in spin-dependent scattering experiments.

Deuterium Isotope Effects on Retention

The substitution of hydrogen with deuterium in the alkyl chain of pentanol reduces the dispersion interactions in hydrophobic stationary phases [1]. Chromatographic studies measuring the Total Isotope Effect (TIE) show a reduction in the retention factor (k) for 1-pentan-d11-ol compared to unlabeled 1-pentanol. This kH/kD ratio allows analytical chemists to calculate direct free energy changes associated with hydrophobic partitioning [1].

Procuring the exact D11 isotopologue enables the measurement of baseline thermodynamic properties in separation science.

Internal Standard for VOC Analysis

Used in environmental and food testing labs via GC-MS to accurately quantify pentanol and related short-chain alcohols, relying on the +11 Da shift to eliminate matrix interference [1].

Nanostructured Cleaning Fluid Analysis

Applied in materials science to study the nanostructure of surfactant-based cleaning systems (e.g., SDS/pentanol/water) using SANS contrast matching [2].

Polarized Target for Spin Physics

Procured by national accelerator facilities as a solid target material, where its >50% deuteron polarization under 5.0 T fields enables advanced neutron scattering investigations [3].