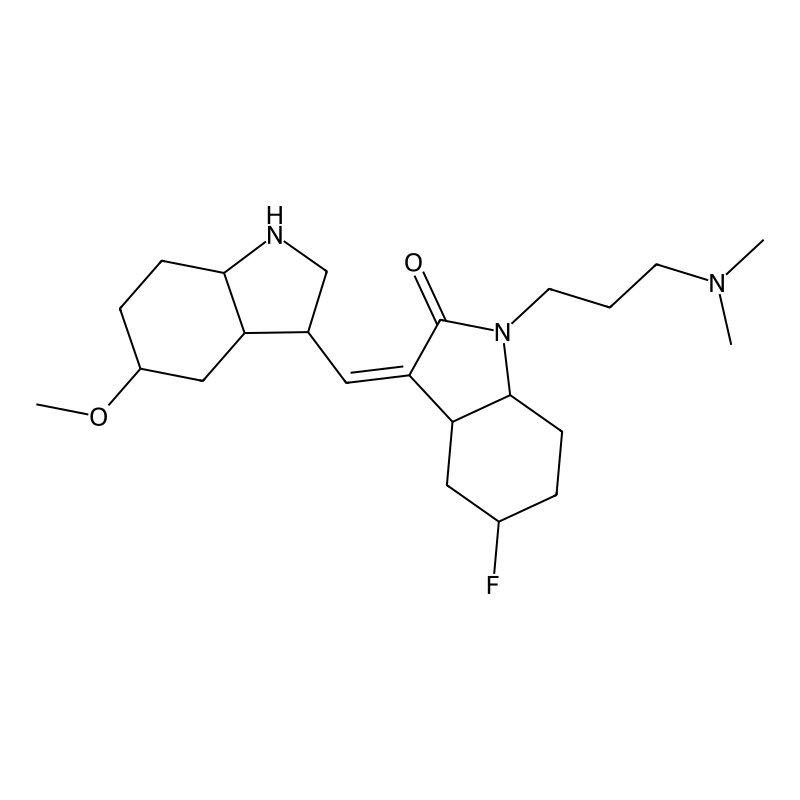
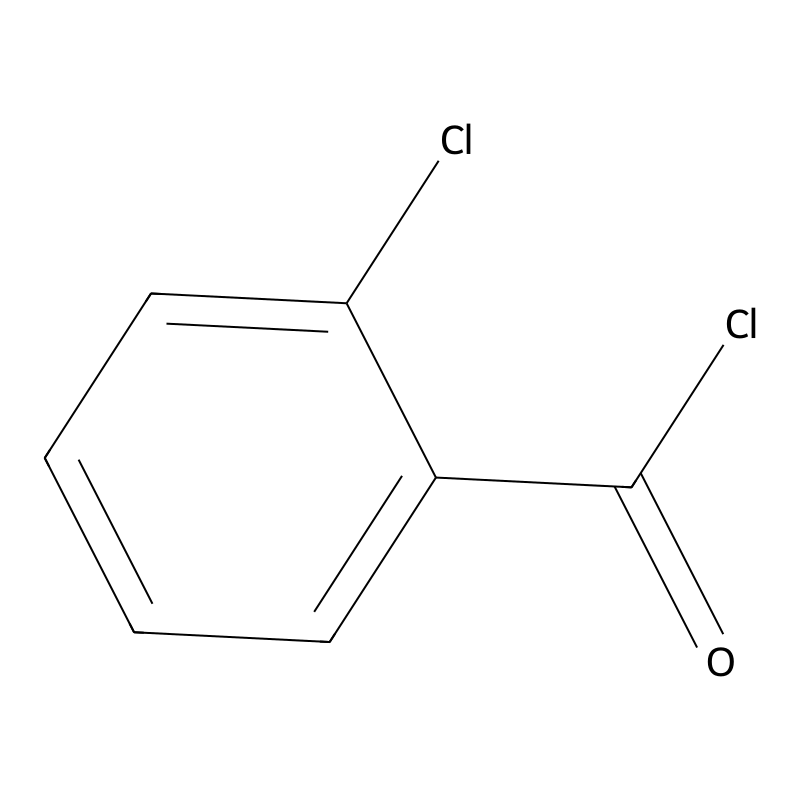
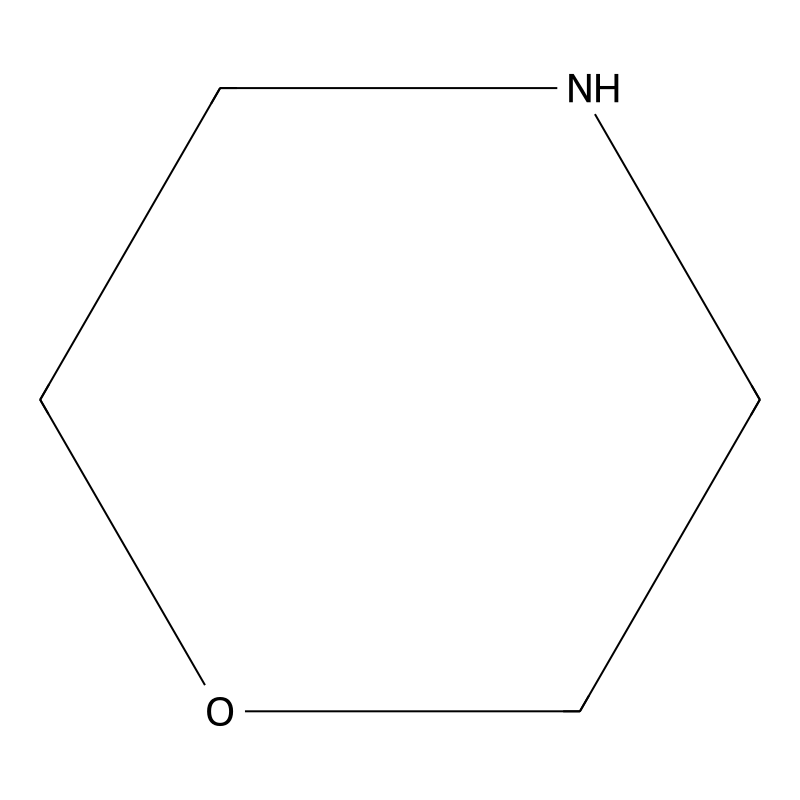
Morpholine

Polymer-bound morpholine (CAS 138048-80-3) is a solid-supported tertiary amine reagent, typically formulated as a macroporous or gel-type polystyrene resin functionalized with morpholine end groups[1]. Functioning as an immobilized equivalent to liquid N-methylmorpholine (NMM), it is primarily procured as an acid scavenger and basic catalyst for amide, sulfonamide, and peptide synthesis workflows [1]. By anchoring the basic moiety to an insoluble matrix, this reagent enables the sequestration of acidic byproducts (such as HCl) directly onto the resin, allowing for product isolation via simple physical filtration [1]. This physical property eliminates the need for aqueous workup or chromatographic purification, making it a critical material for high-throughput parallel synthesis and automated combinatorial chemistry.

Substituting polymer-bound morpholine with its liquid analogs, such as N-methylmorpholine (NMM) or triethylamine (TEA), introduces significant downstream processing bottlenecks in parallel synthesis [1]. Liquid bases form soluble hydrochloride salts during acylation or sulfonylation, necessitating liquid-liquid extraction or flash chromatography to isolate the target compound [1]. In high-throughput environments, this manual workup reduces throughput and increases solvent consumption drastically. Furthermore, volatile liquid amines pose inhalation hazards and require fume hood handling due to their strong odors, whereas the polymer-bound resin is odorless, non-volatile, and can be dosed cleanly by weight, ensuring exact stoichiometric control without the risk of atmospheric degradation[1].

Downstream Purification Efficiency: Filtration vs. Chromatography

In parallel amide and sulfonamide synthesis, the use of polymer-bound morpholine eliminates the need for chromatographic purification[1]. When reacting sulfonyl chlorides with amines, utilizing the polymer-supported base allows the acidic byproducts to be sequestered on the resin [1]. Quantitative isolation of the product is achieved via simple filtration, typically yielding crude purities of >90–95% directly from the filtrate [1]. In contrast, using liquid N-methylmorpholine (NMM) leaves soluble salts in the reaction mixture, requiring aqueous extraction and column chromatography, extending workup time from minutes to several hours per sample.

Procuring the polymer-bound resin directly translates to massive labor and solvent savings in high-throughput medicinal chemistry laboratories.

Acid Scavenging Capacity and Stoichiometric Control

Polymer-bound morpholine resins are commercially available with high loading capacities, typically ranging from 2.75 to 3.6 mmol/g [1]. This high functional density allows for the use of a minimal mass of resin to achieve a 2- to 4-fold molar excess of base, driving sluggish acylation reactions to completion without contaminating the product stream [1]. Unlike liquid bases, where an excess remains in solution and complicates isolation, an excess of the polymer-bound reagent simply remains insoluble [1]. Studies demonstrate that using 3-4 equivalents of polymer-bound morpholine ensures complete scavenging of generated HCl, whereas a similar excess of liquid triethylamine requires extensive acidic aqueous washing to remove.

Allows chemists to use large excesses of base to force reactions to completion without paying a penalty in purification difficulty.

Volatility and Handling Safety in Automated Workflows

Liquid morpholine and N-methylmorpholine possess significant vapor pressures (e.g., morpholine vapor pressure is ~10 mmHg at 20 °C) and highly objectionable ammonia-like odors, requiring strict fume hood handling . Polymer-bound morpholine, formulated as a cross-linked polystyrene matrix, has an effective vapor pressure of zero. It is an odorless, free-flowing solid that can be weighed openly on a benchtop. This physical state completely eliminates inhalation exposure risks and allows for precise gravimetric dispensing, which is critical for automated solid-phase synthesizers where liquid dispensing of volatile bases can lead to needle clogging or inaccurate dosing .

Enhances laboratory safety and enables precise, automated solid-dispensing workflows without specialized ventilation.

Automated Parallel Synthesis of Compound Libraries

Where this compound is the right choice for high-throughput medicinal chemistry, allowing rapid generation of amide and sulfonamide libraries by eliminating liquid-liquid extraction bottlenecks and enabling direct-to-assay filtrate use[1].

Scavenging Acidic Byproducts in Water-Sensitive Reactions

Where this compound is the right choice for sequestering HCl or other acids in reaction mixtures where traditional aqueous workup would hydrolyze or degrade water-sensitive intermediates[1].

Solid-Phase Peptide Synthesis (SPPS) Additive

Where this compound is the right choice as an immobilized base to neutralize trace acids or facilitate coupling without introducing soluble basic contaminants that might cause racemization of the peptide chain[2].