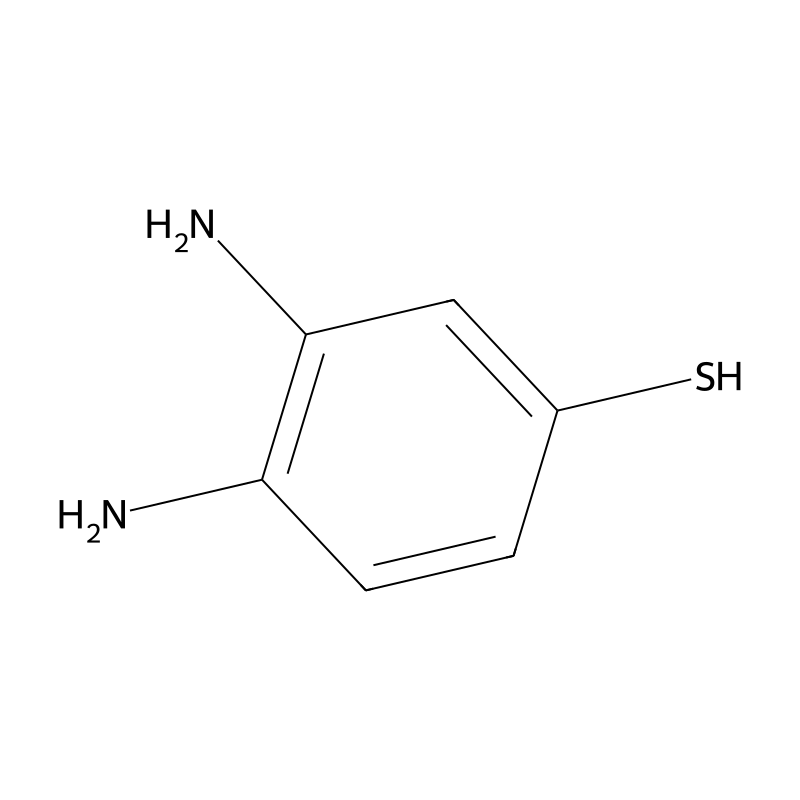
3,4-Diaminobenzenethiol

3,4-Diaminobenzenethiol (CAS: 655247-00-0) is a highly specialized bifunctional aromatic building block featuring an ortho-diamine moiety and a reactive thiol group. In materials science and chemoinformatics, this specific functional combination is critical for designing surface-anchored sensors, self-assembled monolayers (SAMs), and functionalized metal nanoparticles [1]. The thiol group provides robust covalent anchoring to gold and silver surfaces via strong metal-sulfur bonds, while the ortho-diamine serves as a highly selective recognition site for nitric oxide (NO) and specific metal cations like Cu2+, as well as a condensation precursor for quinoxalines and benzimidazoles [2]. For industrial and laboratory procurement, its value lies in eliminating the need for multi-step conjugations by providing both surface-binding and target-recognition capabilities in a single compact molecule.

Procurement of generic diamines (such as 1,2-phenylenediamine) or generic aminothiols (such as 4-aminothiophenol) cannot replicate the dual-action performance of 3,4-diaminobenzenethiol. While 1,2-phenylenediamine can react with NO to form benzotriazoles, it lacks the thiol anchor required for surface-enhanced Raman scattering (SERS) or nanoparticle functionalization, leading to probe leaching or complete failure to assemble on noble metals [1]. Conversely, 4-aminothiophenol readily forms self-assembled monolayers on gold and silver but lacks the adjacent amine required to form the triazole ring, rendering it completely unresponsive to NO [1]. For applications requiring both surface immobilization and ortho-diamine reactivity, 3,4-diaminobenzenethiol is the non-interchangeable, procurement-critical choice.

Ratiometric SERS Detection of Nitric Oxide (NO) via Surface Anchoring

3,4-Diaminobenzenethiol enables the construction of ratiometric SERS nanoprobes because it anchors to silver/gold via the thiol group while leaving the ortho-diamine free to react with NO. Upon NO exposure, it forms a triazole ring, generating a new Raman peak at 541 cm⁻¹ while the C-S reference peak at 1078 cm⁻¹ remains stable, allowing quantitative detection with a limit of 3.89 nmol/L[1]. Comparatively, 1,2-phenylenediamine cannot form stable Ag-S bonds, preventing the generation of a stable SERS signal, while 4-aminothiophenol cannot form the triazole ring, yielding zero NO-specific ratiometric response [1].

For researchers developing implantable or cellular SERS sensors, this compound is mandatory to achieve both stable metallic immobilization and selective NO recognition, ensuring mainstream laboratory workflow fit.

Colorimetric Detection of Copper Ions (Cu2+) via Nanoparticle Aggregation

3,4-Diaminobenzenethiol acts as a highly specific ligand for gold nanoparticles (AuNPs) in the colorimetric detection of Cu2+. The unique coordination geometry provided by the combination of the thiol (for AuNP attachment) and the ortho-diamine (for Cu2+ chelation) allows for rapid, visible color changes proportional to Cu2+ concentration [1]. Assays utilizing this compound demonstrate a linear detection range of 0.5 μM to 2.0 μM with recoveries of 92–109%[1]. In contrast, generic thiols like 4-aminothiophenol lack the specific bidentate amine coordination environment, resulting in lower selectivity against competing heavy metal ions and failing to induce the required specific aggregation.

Procurement for environmental testing or assay development should prioritize this compound to simplify assay design and eliminate the need for multi-step nanoparticle functionalization.

Synthesis of NIR-II Fluorescent Nanoprobes via Nucleophilic Substitution

The bifunctionality of 3,4-Diaminobenzenethiol allows it to be coupled with cyanine dyes (e.g., IR 1061) to create NO-responsive near-infrared (NIR-II) probes. The ortho-diamine acts as an electron donor, quenching the dye via photoinduced electron transfer (PET) [1]. Upon reaction with NO, the PET is inhibited, resulting in a massive fluorescence recovery. Studies show that the resulting probe exhibits a 9.2-fold fluorescence increment at 1050 nm upon NO treatment [1]. The presence of the thiol group provides a synthetic handle for further nucleophilic substitution that standard 1,2-phenylenediamine lacks, enabling integration into complex nanocarriers like mesoporous silica nanoparticles.

For in vivo imaging and diagnostic procurement, this compound provides both the NO-responsive switch and the chemical handle needed for advanced nanocarrier integration, proving its superior precursor suitability.

Ratiometric SERS Biosensors

Ideal for manufacturing silver- or gold-based SERS nanoprobes for real-time, low-concentration tracking of nitric oxide in live cells or tissues, leveraging the compound's dual anchoring and sensing capabilities [1].

Environmental Colorimetric Assays

Used as a primary ligand for gold nanoparticles to create rapid, naked-eye or UV-Vis quantifiable detection kits for Cu2+ in water samples, avoiding the need for multi-step functionalization[2].

Advanced Diagnostic Imaging Precursors

Serves as the reactive core for synthesizing NIR-II fluorescent probes used in monitoring drug-induced liver injury (DILI) or other NO-related pathologies, utilizing its PET quenching mechanism and synthetic modularity[3].