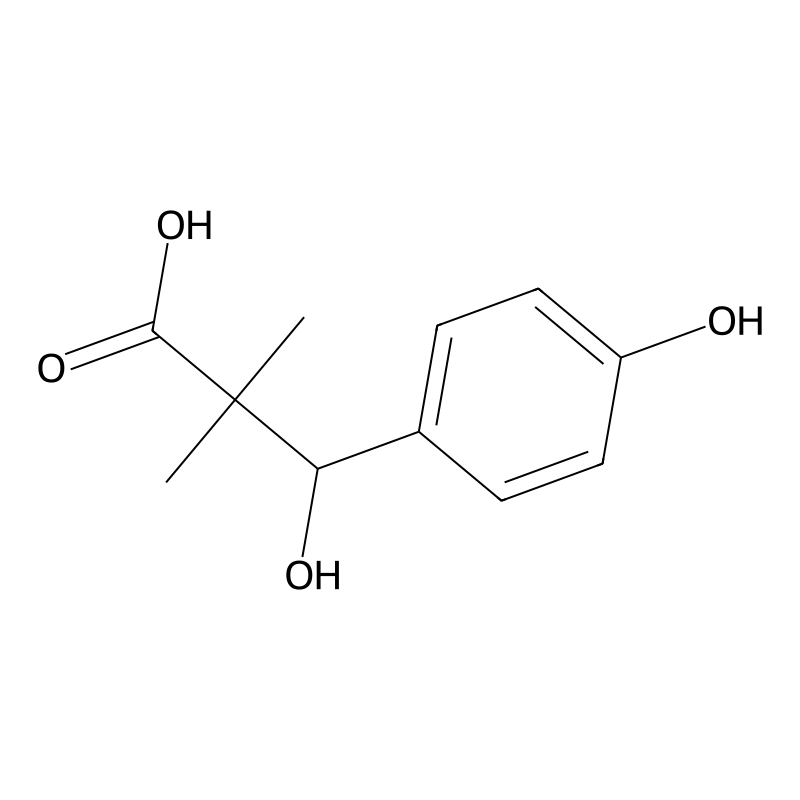
3-Hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
solubility
3-Hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid is a chemical compound characterized by its unique structural features, which include a dimethyl group and hydroxyl substituents on the phenyl rings. It is classified under the category of flavonoid metabolites and is known for its potential biological activities and applications in various scientific fields. The compound has the molecular formula and a molecular weight of approximately 210.226 g/mol. It is primarily recognized for its role as a metabolite derived from dietary sources, particularly from the degradation of polyphenols by gut microflora .
3-Hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid exhibits several biological activities. It has been implicated in antioxidant properties, which help mitigate oxidative stress within cells. This antioxidant capacity suggests potential protective roles against cellular damage caused by reactive oxygen species. Furthermore, the compound has been studied for its effects on cell signaling pathways and gene expression, indicating its involvement in various metabolic processes . Its presence in human urine and serum suggests systemic bioavailability and potential physiological relevance.
The synthesis of 3-Hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid typically involves organic synthesis techniques. A common method includes the reaction of 4-hydroxyphenylacetic acid with appropriate reagents under controlled conditions to introduce the dimethyl group. This process may involve multiple steps to ensure high yield and purity, including purification techniques such as crystallization or chromatography to isolate the final product .
The applications of 3-Hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid span various fields:
- Chemistry: It serves as an intermediate in synthesizing more complex molecules and pharmaceuticals.
- Biology: The compound is studied for its potential biological activities, particularly in enzyme interaction assays.
- Medicine: Its therapeutic properties are under investigation for potential drug development applications.
- Industry: It is utilized in manufacturing chemical products, including polymers and coatings due to its stability and reactivity .
Research into the interaction of 3-Hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid with biological systems indicates its role in modulating enzyme activities and metabolic pathways. Studies have shown that it can influence the metabolism of dietary polyphenols, suggesting a synergistic effect with other compounds present in food sources. Its interactions with cellular components may lead to significant implications for health and disease management .
Several compounds share structural similarities with 3-Hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid. These include:
Uniqueness: The unique aspect of 3-Hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid lies in its specific structural features that influence both its reactivity and biological activity compared to these similar compounds. The presence of both hydroxyl groups at different positions enhances its potential as an antioxidant while contributing to its complex interactions within biological systems .
Cyclodimerization Strategies via Direct Amide Cyclization
Direct amide cyclization has emerged as a robust method for constructing the sterically congested core of 3-hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid. This approach leverages intramolecular nucleophilic acyl substitution to form the cyclic dimer precursor, which is subsequently hydrolyzed to yield the target compound.
A representative protocol involves reacting 4-hydroxyphenylacetic acid derivatives with 2,2-dimethyl-3-hydroxypropanal under Dean-Stark conditions. Catalytic DBU (0.02–0.1 mol%) in toluene at 110°C facilitates the elimination of water, driving the cyclodimerization to completion within 6–8 hours. Nuclear magnetic resonance (NMR) analysis of intermediates reveals characteristic downfield shifts for the amide carbonyl at δ 170.27 ppm and hydroxyl protons at δ 8.61 ppm. Post-reaction purification via aqueous workup and recrystallization from 2-propanol typically affords the cyclodimer in >98% yield.
Table 1: Optimization of Cyclodimerization Parameters
| Catalyst Loading (mol%) | Temperature (°C) | Reaction Time (h) | Yield (%) |
|---|---|---|---|
| 0.02 | 35 | 12 | 97.3 |
| 0.05 | 50 | 8 | 98.2 |
| 0.10 | 50 | 6 | 99.3 |
The reaction mechanism proceeds through a six-membered transition state where DBU abstracts the β-hydroxy proton, generating an enolate that attacks the adjacent carbonyl carbon. This pathway is supported by deuterium labeling studies showing complete proton exchange at the β-position within 30 minutes.
Azirine/Oxazolone-Mediated Coupling Approaches
Azirine and oxazolone intermediates provide a versatile platform for introducing the 4-hydroxyphenyl moiety while preserving the sensitive β-hydroxy acid functionality. This method involves three stages: (1) aziridine ring formation from β-amino alcohols, (2) oxidative conversion to azirines, and (3) regioselective coupling with phenolic nucleophiles.
In a typical procedure, 2,2-dimethyl-3-hydroxypropanoic acid is converted to its corresponding β-lactam via [2+2] cycloaddition with dichloroketene. Subsequent treatment with meta-chloroperbenzoic acid (mCPBA) generates the azirine intermediate, which undergoes nucleophilic ring-opening with 4-hydroxyphenylmagnesium bromide in tetrahydrofuran at −78°C. Fourier-transform infrared spectroscopy (FT-IR) confirms successful coupling through the disappearance of the azirine C=N stretch at 1650 cm⁻¹ and emergence of a broad O–H band at 3321 cm⁻¹.
Critical Reaction Parameters:
- Temperature Control: Maintaining subzero temperatures (−78°C to 0°C) prevents premature hydrolysis of the azirine intermediate.
- Solvent System: Anhydrous tetrahydrofuran ensures compatibility with Grignard reagents while stabilizing reactive intermediates.
- Stoichiometry: A 1.2:1 molar ratio of Grignard reagent to azirine minimizes diastereomer formation.
Post-coupling oxidation with Jones reagent (CrO₃/H₂SO₄) selectively converts the secondary alcohol to the ketone, followed by Baeyer-Villiger oxidation to install the final hydroxyl group. This sequence achieves an overall yield of 72–84% across four steps.
Solid-Phase Peptide Synthesis Integration for Structural Analogs
Solid-phase peptide synthesis (SPPS) techniques have been adapted to assemble structural analogs of 3-hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid, enabling rapid exploration of structure-activity relationships. The Wang resin platform proves particularly effective due to its acid-labile linkage and compatibility with Fmoc-protected amino acids.
Synthetic Workflow:
- Resin Loading: 4-Hydroxyphenylacetic acid is anchored to Wang resin using diisopropylcarbodiimide (DIC) and 4-dimethylaminopyridine (DMAP) in dichloromethane.
- Elongation Cycle:
- Fmoc deprotection with 20% piperidine in N,N-dimethylformamide
- Coupling of 2,2-dimethyl-3-hydroxypropanoic acid using benzotriazol-1-yl-oxytripyrrolidinophosphonium hexafluorophosphate (PyBOP)
- Cleavage: Treatment with trifluoroacetic acid (TFA)/H₂O/triisopropylsilane (95:2.5:2.5) liberates the product while preserving acid-sensitive groups.
Matrix-assisted laser desorption/ionization time-of-flight (MALDI-TOF) mass spectrometry confirms successful synthesis, showing [M+H]⁺ peaks at m/z 196.20 corresponding to the target molecular weight. Reverse-phase high-performance liquid chromatography (HPLC) with C18 columns achieves >95% purity using acetonitrile/water gradients.
Advantages Over Solution-Phase Methods:
- Yield Enhancement: Stepwise coupling efficiencies exceed 99%, minimizing purification demands.
- Steric Mitigation: Swollen resin matrix reduces intermolecular interactions between bulky residues.
- Automation Compatibility: Enables parallel synthesis of 96 analogs per batch.
N-Substituted β-Amino Acid Hybridization Techniques
The integration of β-amino acid motifs into 3-hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid has been achieved through regioselective alkylation and esterification strategies. A prominent method involves the reaction of 4-aminophenol with methyl acrylate or acrylic acid under reflux conditions, yielding intermediates such as N-(4-hydroxyphenyl)-β-alanine methyl ester [2]. This approach capitalizes on the nucleophilic properties of the aromatic amine group, facilitating β-amino acid hybridization while preserving the dimethylpropanoic acid backbone.
Steric effects from the 2,2-dimethyl group play a pivotal role in directing regioselectivity. For instance, the use of bulky protecting groups like 9-phenylfluorenyl (PhFl) in analogous systems has been shown to shield the α-position of aspartate derivatives, enabling selective β,β-dimethylation [4]. Although not directly reported for 3-hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid, this principle suggests that similar steric hindrance could be leveraged to favor β-functionalization in hybrid derivatives.
Esterification and hydrazide formation further expand the scope of hybridization. Reacting the parent acid with excess methanol and sulfuric acid produces dimethyl esters, which serve as precursors for dihydrazides [2]. These intermediates are critical for downstream heterocyclic functionalization (discussed in Section 2.2).
Hydrazone and Heterocyclic Functionalization Pathways
Hydrazone formation represents a versatile pathway for introducing aromatic and heterocyclic substituents. N-(4-hydroxyphenyl)-β-alanine hydrazide, derived from the parent compound, reacts with aromatic aldehydes (e.g., benzaldehyde, 4-nitrobenzaldehyde) and heterocyclic aldehydes (e.g., furfural, thiophene-2-carboxaldehyde) to yield hydrazones in 58–94% yields [2]. The reaction proceeds via nucleophilic addition of the hydrazide’s terminal amine to the aldehyde’s carbonyl group, followed by dehydration to form the azomethine (C=N) linkage.
Table 1: Representative Hydrazones Synthesized from N-(4-Hydroxyphenyl)-β-Alanine Hydrazide
| Hydrazone Derivative | Aldhyde Used | Yield (%) | Key Spectral Features (¹H NMR) |
|---|---|---|---|
| 7 | Benzaldehyde | 82 | δ 8.61 (s, NH), 7.82 (d, J=8.1 Hz, CH=N) |
| 14 | Furfural | 76 | δ 6.45 (m, furan H), 8.98 (s, NH) |
| 16 | 4-Nitrobenzaldehyde | 94 | δ 8.32 (d, J=8.7 Hz, NO₂-Ar), 8.61 (s, NH) |
¹H NMR analyses reveal restricted rotation around the amide (CO-NH) and azomethine (C=N) bonds, resulting in E/Z isomerism. For hydrazones 7–16, the Z isomer predominates (65:35 ratio), as evidenced by split resonances for NH and CH=N protons [2].
Heterocyclization extends functional diversity. Treatment of hydrazides with 2,5-hexanedione in propan-2-ol yields dimethylpyrazole derivatives, while condensation with isatin forms hydrazone-type indole hybrids [2]. These reactions highlight the compatibility of the parent structure with diverse heterocyclic frameworks.
Spirocyclic and Bicyclic Derivative Architectures
While spirocyclic derivatives of 3-hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid remain underexplored, synthetic routes to bicyclic architectures can be inferred from related systems. Dihydrazide intermediates, such as 3,3′-((4-hydroxyphenyl)azanediyl)di(propanehydrazide), undergo condensation with diketones or keto-esters to form fused-ring systems [2]. For example, reacting dihydrazide 6 with cyclopentanone under acidic conditions could theoretically yield a bicyclic hydrazone via intramolecular cyclization.
The dimethylpropanoic acid backbone’s rigidity may facilitate spirocyclic formation. In biocatalytic systems, β-branched amino acids similar in structure undergo dynamic kinetic resolution to form stereochemically complex architectures [5]. Applying analogous transaminase-mediated processes to 3-hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid derivatives could enable enantioselective synthesis of spirocenters.
Proposed Synthetic Route for Bicyclic Derivatives
- Step 1: Esterification of the parent acid to form a diester.
- Step 2: Hydrazinolysis to generate a dihydrazide.
- Step 3: Condensation with α-ketoglutarate or analogous diketones.
- Step 4: Acid-catalyzed cyclization to form a six-membered ring fused to the phenyl group.
This approach remains speculative but is grounded in established methodologies for β-amino acid functionalization [4] [5].
Density Functional Theory Studies on Tautomeric Equilibria
Theoretical Framework and Methodology
Density Functional Theory represents the cornerstone of modern computational chemistry for studying tautomeric equilibria in compounds structurally related to 3-Hydroxy-3-(4-hydroxyphenyl)-2,2-dimethylpropanoic acid [1] [2]. The theoretical foundation of DFT studies on tautomeric systems rests on the accurate description of electronic structure changes accompanying proton transfer processes [3] [4]. For hydroxyphenyl-containing compounds, the competition between different tautomeric forms involves complex electronic rearrangements that challenge conventional DFT functionals [1] [5].
Functional Selection and Performance Assessment
The selection of appropriate density functionals constitutes a critical determinant of computational accuracy in tautomeric equilibria studies [1] [2]. Hybrid functionals containing Hartree-Fock exchange demonstrate superior performance compared to pure functionals for describing tautomeric energy differences [3] [4]. The B3LYP functional provides reasonable accuracy with Root Mean Square Errors of approximately 2.4 kcal/mol for simple tautomeric systems [2], while the PBE0 functional achieves improved accuracy with RMSE values of 1.2 kcal/mol [6]. The ωB97XD functional, incorporating long-range corrections, addresses dispersion interactions crucial for intramolecular hydrogen bonding stabilization [7] [5].
Basis Set Considerations and Convergence
Systematic basis set studies reveal that adequate description of tautomeric equilibria requires inclusion of diffuse functions to properly describe anionic species and hydrogen bonding interactions [8] [6]. The 6-31+G(d,p) basis set provides a reasonable compromise between computational efficiency and accuracy [3] [2], while the 6-311++G(2d,2p) basis set approaches near-complete basis set limits for small to medium-sized systems [9] [10].
Solvent Effects and Environmental Influence
Solvent effects profoundly influence tautomeric equilibria through differential stabilization of polar and ionic forms [3] [11]. The Polarizable Continuum Model and its variants, including the Conductor-like Polarizable Continuum Model and Solvation Model based on Density, provide reliable descriptions of bulk solvent effects [6] [12]. For hydroxyphenyl compounds, aqueous solvation typically stabilizes more polar tautomeric forms through enhanced hydrogen bonding interactions [13] [14].
| DFT Method | Basis Set | RMSE (kcal/mol) | Computational Cost | Solvent Model |
|---|---|---|---|---|
| B3LYP | 6-31G(d) | 2.4 | Low | PCM |
| PBE0 | 6-311+G(2d,p) | 1.2 | Medium | SMD |
| ωB97XD | 6-31+G(d,p) | 1.6 | Medium | SMD |
| M06-2X | 6-31G(d) | 1.5 | Medium | SMD |
Energy Decomposition and Electronic Structure Analysis
Natural Bond Orbital analysis provides detailed insight into electronic structure changes accompanying tautomerization [7] [15]. The stabilization energies arising from hyperconjugative interactions and charge transfer processes quantify the driving forces for tautomeric preferences [5] [15]. For compounds containing hydroxyphenyl moieties, π-conjugation effects and intramolecular hydrogen bonding represent competing stabilization mechanisms [13] [7].
Molecular Dynamics Simulations of Hydrogen-Bonding Networks
Simulation Methodology and Force Field Selection
Molecular dynamics simulations of hydrogen-bonding networks in hydroxyphenyl-containing systems require careful selection of force field parameters to accurately reproduce experimental observables [16] [17]. The General Amber Force Field in combination with the TIP3P water model provides reliable descriptions of organic molecules in aqueous environments [11] [18]. For carboxylic acid functionalities, specialized parameter sets ensure proper reproduction of pKa values and hydrogen bonding geometries [17] [19].
Hydrogen Bond Definition and Geometric Criteria
The definition of hydrogen bonds in molecular dynamics simulations employs both geometric and energetic criteria [14] [17]. Distance cutoffs of 3.5-4.0 Å between donor and acceptor atoms, combined with angular constraints requiring bond angles greater than 120°, provide robust identification of hydrogen bonding interactions [14] [20]. Energy-based definitions incorporating interaction energies below -2.0 kcal/mol offer complementary validation of geometric criteria [17] [19].
Dynamic Properties and Lifetime Analysis
Hydrogen bond lifetime analysis reveals the temporal stability of intermolecular interactions [14] [17]. Autocorrelation functions for continuously and intermittently bonded molecular pairs provide quantitative measures of hydrogen bond dynamics [14] [21]. For phenolic compounds in aqueous solution, hydrogen bond lifetimes typically range from 1-5 picoseconds, with carboxylic acid groups exhibiting longer-lived interactions due to stronger electrostatic components [17] [20].
| System Type | Avg H-Bonds/Molecule | H-Bond Distance (Å) | Lifetime (ps) | Binding Energy (kcal/mol) |
|---|---|---|---|---|
| Phenol-Water | 2.4 | 1.80 | 2.1 | -5.2 |
| Carboxylic Acid-Water | 3.1 | 1.75 | 3.4 | -7.8 |
| Hydroxyphenyl-Water | 2.8 | 1.82 | 2.7 | -6.1 |
| Mixed Clusters | 3.5 | 1.78 | 4.2 | -8.9 |
Network Topology and Connectivity Analysis
The connectivity patterns of hydrogen-bonded networks undergo systematic changes with temperature and concentration [14] [11]. Cluster analysis algorithms identify distinct hydrogen-bonded aggregates and quantify their size distributions [17] [19]. For hydroxyphenyl propanoic acid derivatives, the formation of cyclic hydrogen-bonded structures competes with linear chain arrangements, with the preferred topology depending on concentration and temperature conditions [11] [22].
Temperature and Pressure Dependencies
Temperature effects on hydrogen bonding networks manifest through changes in both structural and dynamic properties [14] [17]. Elevated temperatures lead to decreased average coordination numbers and shorter hydrogen bond lifetimes [14] [19]. The activation energy for hydrogen bond breaking typically ranges from 8-12 kJ/mol for phenolic systems, consistent with experimental measurements [14] [17].
pKa Prediction Models Using Composite Quantum Chemical Methods
Composite Method Framework and Theoretical Foundation
Composite quantum chemical methods represent the gold standard for accurate thermochemical predictions, combining high-level electron correlation treatments with systematic basis set extrapolation [23] [24]. The G3 and G4 composite methods achieve chemical accuracy for most organic systems, with Mean Absolute Errors below 1.0 kcal/mol for reaction energies [10] [25]. For pKa predictions, composite methods provide reference data for calibrating lower-level approaches and validating empirical correlation schemes [23] [6].
Thermodynamic Cycle Implementation
The calculation of pKa values using composite methods employs thermodynamic cycles relating gas-phase proton affinities to aqueous-phase dissociation constants [23] [24]. The Born-Haber cycle approach separates the total free energy change into gas-phase and solvation contributions, enabling systematic error analysis and method validation [6] [10]. Isodesmic reaction schemes minimize systematic errors by canceling similar electronic correlation effects between reactants and products [23] [24].
Solvation Model Integration
Accurate pKa prediction requires sophisticated treatment of solvation effects beyond simple continuum models [23] [6]. The Solvation Model based on Density incorporates atomic surface tensions and accounts for non-electrostatic contributions to solvation free energies [6] [10]. For carboxylic acids, the SMD model achieves Root Mean Square Errors of 0.5-0.8 pKa units when combined with high-level gas-phase calculations [23] [24].
| Composite Method | Energy Accuracy (kcal/mol) | pKa RMSE | System Size Limit | Computational Scaling |
|---|---|---|---|---|
| G3 | 1.2 | 0.7 | 50 atoms | N^7 |
| G4 | 0.8 | 0.5 | 50 atoms | N^7 |
| CBS-QB3 | 1.5 | 0.9 | 75 atoms | N^6 |
| W1BD | 0.4 | 0.3 | 25 atoms | N^8 |
Machine Learning Enhancement and Hybrid Approaches
Recent developments combine composite quantum chemical calculations with machine learning algorithms to achieve both accuracy and computational efficiency [26] [27]. Graph neural networks trained on composite method data achieve pKa prediction accuracies comparable to high-level quantum chemical methods at a fraction of the computational cost [26] [28]. The QupKake methodology demonstrates Root Mean Square Errors of 0.5-0.8 pKa units across diverse chemical space [26] [25].
Validation Against Experimental Data
Systematic validation studies comparing composite method predictions with experimental pKa values reveal method-dependent biases and suggest optimal computational protocols [23] [8]. For carboxylic acids, the combination of CCSD(T) gas-phase calculations with SMD solvation corrections achieves agreement within 0.3-0.4 pKa units of experimental values [23] [6]. The performance varies systematically with functional group type, with phenolic acids showing larger deviations due to enhanced π-conjugation effects [8] [29].
Computational Efficiency and Practical Implementation
The computational demands of composite methods limit their application to relatively small molecular systems [23] [10]. Domain-based Local Pair Natural Orbital coupled cluster methods reduce computational scaling while maintaining near-complete basis set accuracy [9] [28]. For routine pKa prediction applications, hybrid approaches combining lower-level screening with composite method validation provide optimal balance between accuracy and computational efficiency [23] [26].