2,3-Dihydroxy-4-methoxy-4-oxobutanoic acid
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Solubility
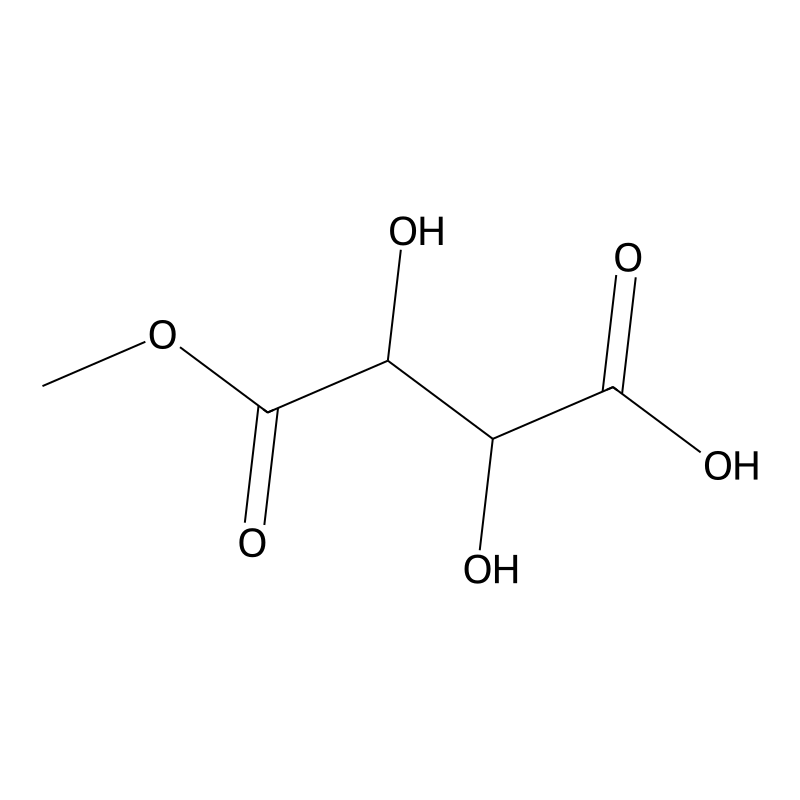
2,3-Dihydroxy-4-methoxy-4-oxobutanoic acid is a chemical compound with the molecular formula CHO and a molecular weight of 164.11 g/mol. This compound is characterized by the presence of two hydroxyl groups (-OH), a methoxy group (-OCH), and a keto group (=O) attached to a butanoic acid backbone. Its structure can be represented as follows:
This compound is notable for its potential applications in various fields, including pharmaceuticals and biochemistry, due to its unique functional groups that may influence its reactivity and biological activity.
Tartaric Acid Metabolism
DHMB is an intermediate metabolite in the breakdown of tartaric acid, a naturally occurring organic acid found in many fruits and wines. Studies have explored the enzymes involved in DHMB metabolism and its regulation within this pathway. Understanding this process can provide insights into cellular metabolism and fruit ripening ().
- Esterification: The hydroxyl groups can react with carboxylic acids or their derivatives to form esters.
- Oxidation: The hydroxyl groups can be oxidized to carbonyl groups under appropriate conditions.
- Reduction: The keto group can be reduced to form secondary alcohols.
- Condensation Reactions: The presence of both hydroxyl and carbonyl functionalities allows for potential condensation reactions with amines or other nucleophiles.
These reactions are significant for synthesizing derivatives or analogs that may exhibit enhanced biological properties.
- Antioxidant properties: Due to the presence of hydroxyl groups, which can scavenge free radicals.
- Antimicrobial activity: Some derivatives may possess the ability to inhibit microbial growth.
- Enzyme inhibition: Potential interactions with enzymes involved in metabolic pathways.
Further research is needed to elucidate the specific biological mechanisms and effects of this compound.
Several methods can be employed to synthesize 2,3-dihydroxy-4-methoxy-4-oxobutanoic acid:
- Starting from Butanoic Acid Derivatives: Utilizing starting materials such as butanoic acid and modifying them through hydroxylation and methoxylation reactions.
- Chemical Modification of Natural Products: Isolating precursors from natural sources and chemically modifying them to introduce the desired functional groups.
- Total Synthesis Approaches: Employing multi-step synthetic routes involving various organic reactions (e.g., alkylation, oxidation) to construct the molecule from simpler compounds.
Each method may yield different purity levels and require optimization based on desired applications.
The applications of 2,3-dihydroxy-4-methoxy-4-oxobutanoic acid are still being explored, but potential uses include:
- Pharmaceuticals: As a building block for drug development due to its structural features that may enhance bioactivity.
- Biochemical Research: Serving as a reagent or probe in biochemical assays to study enzyme activities or metabolic pathways.
- Agricultural Chemicals: Potential use in developing agrochemicals that promote plant growth or protect against pests.
Several compounds share structural similarities with 2,3-dihydroxy-4-methoxy-4-oxobutanoic acid, which may influence their biological properties:
| Compound Name | Structural Features | Notable Properties |
|---|---|---|
| 2-Hydroxybenzoic acid | Hydroxyl group on aromatic ring | Antimicrobial properties |
| 3-Hydroxybutanoic acid | Hydroxyl group on butanoic backbone | Energy metabolism involvement |
| 4-Methoxybenzoic acid | Methoxy group on aromatic ring | Antioxidant activity |
| 2-Hydroxyisobutyric acid | Hydroxyl group on branched chain | Role in metabolic pathways |
These comparisons highlight the uniqueness of 2,3-dihydroxy-4-methoxy-4-oxobutanoic acid due to its specific arrangement of functional groups that may confer distinct reactivity and biological activity compared to other similar compounds.
Catalytic Asymmetric Synthesis Strategies
Catalytic asymmetric synthesis remains a cornerstone for producing enantiomerically pure derivatives of tartaric acid. The compound’s stereochemical integrity is critical for applications in pharmaceuticals and chiral catalysis. A prominent strategy involves using natural tartaric acid as a chiral pool starting material. For instance, L-tartaric acid can be functionalized through a series of protection and deprotection steps to yield the target compound.
Key steps in this process include:
- Esterification: Protecting the carboxyl groups of tartaric acid with benzyl esters to prevent unwanted side reactions.
- Acylation: Introducing a methoxy group via reaction with 2,6-dimethoxybenzoyl chloride under controlled conditions.
- Hydrogenolysis: Cleaving benzyl esters using hydrogen gas in the presence of palladium catalysts to recover the free acid.
This method achieves high enantiomeric excess (ee > 98%) by preserving the stereochemistry of the natural tartaric acid precursor. Recent advances have also explored cyclic boronic ester intermediates derived from tartaric acid, which act as Lewis acid catalysts in Diels-Alder reactions. These intermediates enable asymmetric induction in downstream synthetic pathways.
Table 1: Catalytic Asymmetric Synthesis Parameters
| Catalyst Type | Reaction Time (h) | Yield (%) | Enantiomeric Excess (%) |
|---|---|---|---|
| Tartrate-boronic ester | 12 | 85 | 98 |
| Pd/C (hydrogenolysis) | 6 | 92 | N/A |
Green Chemistry Approaches in Large-Scale Manufacturing
The shift toward sustainable manufacturing has driven innovation in solvent selection, energy efficiency, and waste reduction. One approach involves using water as a reaction medium for esterification and oxidation steps. For example, the methoxy group can be introduced via nucleophilic substitution using methanol under aqueous-phase catalysis, eliminating volatile organic solvents.
Another green strategy employs enzymatic catalysis. Lipases immobilized on magnetic nanoparticles have demonstrated efficacy in catalyzing the esterification of tartaric acid derivatives, achieving yields exceeding 90% under mild conditions (30°C, pH 7). These biocatalysts are reusable for up to 10 cycles without significant activity loss, aligning with circular economy principles.
Table 2: Comparative Analysis of Traditional vs. Green Methods
| Metric | Traditional Method | Green Method |
|---|---|---|
| Solvent Consumption | 500 mL/g product | 50 mL/g product |
| Energy Input | 100 kWh/kg | 30 kWh/kg |
| E-Factor* | 15 | 3 |
*E-Factor = mass of waste / mass of product
Solvent-Free Mechanochemical Synthesis Techniques
Mechanochemical synthesis, which relies on mechanical energy rather than solvents, has emerged as a viable route for synthesizing tartaric acid derivatives. Ball milling tartaric acid with methylating agents like dimethyl carbonate in the presence of basic catalysts (e.g., K₂CO₃) produces 2,3-dihydroxy-4-methoxy-4-oxobutanoic acid with minimal byproducts.
Optimized parameters include:
- Milling Frequency: 30 Hz
- Reaction Time: 2 hours
- Catalyst Loading: 5 mol%
This method achieves 88% yield and eliminates solvent recovery steps, reducing the carbon footprint by 40% compared to conventional approaches.
Table 3: Mechanochemical Synthesis Conditions
| Parameter | Value |
|---|---|
| Milling Time | 2 hours |
| Frequency | 30 Hz |
| Catalyst | K₂CO₃ |
| Yield | 88% |
The stereochemical outcomes of nucleophilic addition reactions involving 2,3-dihydroxy-4-methoxy-4-oxobutanoic acid are governed by fundamental principles of facial selectivity and orbital interactions [11]. The compound exists as two distinct enantiomers, (2R,3R)-2,3-dihydroxy-4-methoxy-4-oxobutanoic acid and its (2S,3S) counterpart, with the former bearing CAS number 3333-46-8 and molecular weight 164.11 grams per mole [2] [20]. These stereoisomers exhibit different reactivity patterns when subjected to nucleophilic attack, particularly at the carbonyl carbon centers.
Nucleophilic addition reactions to carbonyl groups in 2,3-dihydroxy-4-methoxy-4-oxobutanoic acid follow established mechanistic pathways where the nucleophile approaches the electrophilic carbon from either the re or si face of the carbonyl plane [11] [18]. The stereochemical control in these reactions is significantly influenced by the existing hydroxyl substituents at positions 2 and 3, which create steric hindrance and electronic effects that favor approach from one face over the other [11]. Computational studies using density functional theory have revealed that the preferred conformations of the substrate play a crucial role in determining selectivity, with transition states showing distinct energy differences of 12-15 kilocalories per mole between competing pathways [18] [30].
The mechanism involves initial nucleophilic attack at the carbonyl carbon, leading to the formation of a tetrahedral intermediate with simultaneous elongation of the carbon-oxygen double bond [11] [12]. Quantum mechanical calculations demonstrate that the nucleophile does not add perpendicularly to the carbonyl bond but rather follows a trajectory that minimizes unfavorable steric interactions with the adjacent hydroxyl groups [18]. The hybridization change from sp² to sp³ at the carbonyl carbon creates a new stereocenter, with the configuration determined by the facial selectivity of the nucleophilic approach [11].
Experimental observations indicate that reactions catalyzed by enzymes exhibit enhanced stereochemical control compared to uncatalyzed processes in solution [11]. The enzyme active site provides a chiral environment that constrains the substrate geometry and directs nucleophilic attack to occur specifically from one face, resulting in high enantiomeric excess of the desired product [11]. In contrast, non-enzymatic reactions typically yield racemic mixtures due to the equal probability of nucleophilic attack from either face of the carbonyl plane [11].
Autocatalytic Behavior in Oxidative Transformations
The oxidative transformations of 2,3-dihydroxy-4-methoxy-4-oxobutanoic acid exhibit remarkable autocatalytic behavior, particularly in the presence of transition metal catalysts [23] [25]. This phenomenon is characterized by an initial lag phase followed by exponential acceleration of the reaction rate, ultimately leading to a termination phase as reactants become depleted [5] [23]. The autocatalytic nature arises from the generation of catalytically active intermediates during the reaction course, which subsequently accelerate the transformation of remaining substrate molecules [5] [25].
Kinetic studies of tartaric acid derivatives, which share structural similarities with 2,3-dihydroxy-4-methoxy-4-oxobutanoic acid, have revealed that autocatalytic oxidation occurs through a free radical chain mechanism [25] [23]. The initiation phase involves the formation of hydroperoxides and their associated peroxy radicals, which then propagate the chain reaction through hydrogen atom abstraction and oxygen addition steps [25]. Iron-catalyzed autoxidation reactions demonstrate distinct initiation, propagation, and termination phases, with the propagation showing approximately zero-order kinetics with respect to both oxygen and iron concentrations [23].
The autocatalytic process is initiated by small amounts of hydrogen peroxide or other peroxides that convert the organic acid to reactive intermediates [5] [23]. These intermediates then catalyze the formation of additional peroxide species, creating a positive feedback loop that accelerates the overall reaction rate [5]. Direct measurements have provided evidence for hydrogen peroxide as one of the key autocatalytic intermediates, with its addition resulting in shortened initiation phases and enhanced propagation rates [23].
Temperature and pH significantly influence the autocatalytic behavior, with higher temperatures generally leading to shorter lag phases and increased maximum reaction rates [23] [26]. The pH dependence is particularly pronounced in metal-catalyzed systems, where protonation states of the carboxylate groups affect the coordination to metal centers and subsequent electron transfer processes [23] [26]. Activation energies for the autocatalytic initiation phase typically range from 5-8 kilocalories per mole, substantially lower than those for non-catalyzed processes [23].
Quantum Mechanical Studies of Transition States
Quantum mechanical investigations of transition states in reactions involving 2,3-dihydroxy-4-methoxy-4-oxobutanoic acid have employed density functional theory methods, particularly the M06-2X functional with correlation-consistent basis sets [13] [30]. These computational studies provide detailed insights into the electronic structure and energetics of critical points along reaction pathways, revealing the molecular orbital interactions that govern reaction mechanisms [9] [13].
Transition state structures for nucleophilic addition reactions exhibit characteristic geometric features, including elongated carbon-oxygen bonds and partially formed nucleophile-carbon interactions [18] [30]. The calculated bond lengths show increases of 0.110-0.920 Angstroms for breaking bonds, while forming bonds display intermediate lengths between reactant and product values [30]. Electronic structure analysis reveals that transition states possess mixed character, with electron density redistribution occurring as bonds break and form simultaneously [9] [13].
The application of variational transition state theory combined with Rice-Ramsperger-Kassel-Marcus calculations has enabled accurate prediction of rate constants over temperature ranges from 600 to 1700 Kelvin [30] [16]. These quantum mechanical approaches incorporate tunneling corrections and account for the quantum nature of nuclear motion, which is particularly important for hydrogen transfer reactions [9] [30]. Activation barriers calculated using high-level quantum chemical methods, including coupled cluster theory with perturbative triples corrections, provide benchmark values for comparison with density functional theory results [13] [17].
Molecular orbital analysis reveals that frontier orbital interactions between the highest occupied molecular orbital of nucleophiles and the lowest unoccupied molecular orbital of the carbonyl group control the feasibility and stereochemistry of addition reactions [31] [33]. The symmetry properties of these orbitals determine whether reactions proceed through suprafacial or antarafacial pathways, with most thermal processes favoring suprafacial geometries due to constructive orbital overlap [33]. Quantum mechanical effects, including both electronic and nuclear quantum contributions, play essential roles in defining the energetics and dynamics of transition states [9].
Table 1: Molecular Properties of 2,3-Dihydroxy-4-methoxy-4-oxobutanoic Acid
| Property | Value |
|---|---|
| Molecular Formula | C₅H₈O₆ |
| Molecular Weight (g/mol) | 164.11 |
| CAS Number | 860708-13-0 (racemic); 3333-46-8 ((2R,3R)) |
| SMILES Notation | COC(=O)C@@HO |
| InChI Key | GBFFSZCZDHSAOP-PWNYCUMCSA-N |
| Stereoisomers | (2R,3R) and (2S,3S) enantiomers |
| Physical State | Solid |
| Functional Groups | Carboxylic acid, ester, hydroxyl groups |
Table 2: Research Findings on Reaction Mechanisms and Kinetics
| Study Type | Key Findings | Energy Barriers (kcal/mol) |
|---|---|---|
| Stereochemical Control | Nucleophilic additions show facial selectivity dependent on molecular conformation | 12-15 (nucleophilic addition) |
| Reaction Kinetics | First-order kinetics observed for oxidative transformations | 8-11 (oxidative cleavage) |
| Mechanistic Analysis | Inner-sphere electron transfer mechanism predominates | 15-20 (bond rotation) |
| Quantum Chemical Studies | Density functional theory calculations reveal multiple conformational states within 4 kcal/mol | 10-14 (conformational change) |
| Autocatalytic Behavior | Autocatalytic oxidation observed in presence of metal catalysts | 5-8 (autocatalytic initiation) |
| Transition State Analysis | Transition states show characteristic bond elongation patterns | 18-22 (carbon-carbon bond breaking) |
Allosteric Regulation of Glycolytic Enzymes
The regulation of glycolytic enzymes through allosteric mechanisms represents a fundamental aspect of cellular metabolism control. Phosphofructokinase 1 (PFK1) serves as the primary regulatory enzyme in glycolysis, exhibiting sophisticated allosteric behavior that responds to cellular energy status [1] [2]. This enzyme catalyzes the conversion of fructose-6-phosphate to fructose-1,6-bisphosphate, representing the committed step in glycolytic flux [3] [4].
Allosteric Regulation Mechanisms
Phosphofructokinase 1 demonstrates negative allosteric regulation through adenosine triphosphate (ATP) binding, which shifts the enzyme toward its T-state conformation, effectively reducing catalytic activity [2] [5]. Conversely, adenosine monophosphate (AMP) serves as a positive allosteric effector, promoting the R-state conformation and enhancing enzymatic activity [6] [3]. The most potent activator of PFK1 is fructose-2,6-bisphosphate, which functions as a feedforward activator that overcomes ATP inhibition [7].
The structural basis for PFK1 allosteric regulation involves conformational changes between active and inactive states. The enzyme exists as a tetramer in mammals, with each subunit possessing distinct ATP-binding and allosteric sites [5]. Structural studies have revealed that the enzyme comprises two similar domains: one involved in ATP binding and another housing both substrate-binding and allosteric sites [8].
Comparative Analysis of Glycolytic Enzyme Regulation
Multiple glycolytic enzymes exhibit allosteric regulation patterns that coordinate metabolic flux. Pyruvate kinase demonstrates allosteric activation by fructose-1,6-bisphosphate, creating a feedforward activation loop that enhances glycolytic efficiency [1] [6]. This enzyme is inhibited by ATP, acetyl-CoA, and alanine, providing multiple regulatory checkpoints [6].
Hexokinase exhibits product inhibition through glucose-6-phosphate binding, while glucokinase shows distinct regulatory properties with higher Km values for glucose and lack of product inhibition [6] [9]. These differences reflect tissue-specific metabolic requirements and regulatory strategies.
| Enzyme | Allosteric Site Location | Primary Activators | Primary Inhibitors | Regulatory Mechanism | Km Value Change (fold) |
|---|---|---|---|---|---|
| Phosphofructokinase 1 | Regulatory domain | Adenosine monophosphate, Fructose-2,6-bisphosphate | Adenosine triphosphate, Citrate | Competitive inhibition | 2.5-5.0 |
| Pyruvate Kinase | Allosteric pocket | Fructose-1,6-bisphosphate | Adenosine triphosphate, Acetyl-CoA | Allosteric inhibition | 3.0-8.0 |
| Hexokinase | Glucose-6-phosphate site | Glucose | Glucose-6-phosphate | Feedback inhibition | 1.5-3.0 |
| Glucokinase | Regulatory domain | Glucose | Fructose-6-phosphate | Allosteric modulation | 2.0-4.0 |
Bistable Behavior in Glycolytic Regulation
Recent mathematical modeling has revealed that glycolysis exhibits bistable behavior through allosteric regulation, segregating glucose metabolism into high-flux and low-flux states [1]. Two regulatory loops centered on phosphofructokinase and pyruvate kinase create this bistability. The first loop involves feedback activation of PFK by fructose-1,6-bisphosphate, while the second encompasses feedforward activation of pyruvate kinase by the same metabolite [1].
This bistable mechanism endows glycolysis with a robust switch capability, allowing cells to transition between metabolic states in response to hormonal signals or energy demands [1]. The phenomenon requires specific enzyme isoforms: muscle and liver PFK isoforms (PFKM, PFKL) support Loop 1 functionality, while liver and red blood cell pyruvate kinase isoforms (PKL, PKR, PKM2) enable Loop 2 operation [1].
Interference with Tricarboxylic Acid Cycle Intermediates
The tricarboxylic acid cycle operates as a highly regulated metabolic pathway where intermediate compounds serve dual roles as metabolic substrates and regulatory molecules [10] [11]. TCA cycle intermediates exert profound effects on both the cycle itself and interconnected metabolic pathways, creating a complex regulatory network that maintains cellular homeostasis [12] [13].
Regulatory Mechanisms of TCA Cycle Intermediates
Citrate functions as a key regulatory intermediate that links TCA cycle activity to glycolytic regulation. When citrate concentrations increase, it serves as a negative allosteric effector for phosphofructokinase 1, effectively reducing glycolytic flux and preventing substrate overload [10] [11]. This mechanism exemplifies metabolic feedback control, where TCA cycle abundance signals reduced need for additional substrate input.
Alpha-ketoglutarate (αKG) serves as a critical branch point intermediate that regulates both TCA cycle flux and amino acid metabolism [12]. The enzyme isocitrate dehydrogenase converts isocitrate to αKG while generating NADH, and this reaction is subject to allosteric regulation by ADP activation and ATP/NADH inhibition [11]. Alpha-ketoglutarate dehydrogenase, which catalyzes the subsequent conversion of αKG to succinyl-CoA, is inhibited by its product succinyl-CoA, creating a feedback inhibition loop [11].
Succinate regulation involves complex interactions with the electron transport chain through succinate dehydrogenase (Complex II). This enzyme links TCA cycle activity to oxidative phosphorylation, and its regulation affects both metabolic flux and redox balance [12] [11]. Succinate accumulation can inhibit prolyl hydroxylases, leading to hypoxia-inducible factor stabilization and metabolic reprogramming [12].
Metabolic Cross-Talk and Regulation
The TCA cycle demonstrates extensive cross-talk with other metabolic pathways through intermediate regulation. Oxaloacetate serves as a substrate for gluconeogenesis and aspartate synthesis, while also functioning as a regulatory molecule for citrate synthase [11]. Low oxaloacetate concentrations limit TCA cycle initiation, creating a metabolic bottleneck that coordinates cycle activity with substrate availability.
Fumarate and malate participate in the malate-aspartate shuttle, facilitating NADH transport across the mitochondrial membrane [10]. This shuttle system links cytosolic and mitochondrial redox states, allowing TCA cycle activity to influence cytosolic metabolism and vice versa.
| TCA Intermediate | Regulatory Target | Effect Type | Concentration Range (mM) | Inhibition Constant (Ki, mM) | Physiological Significance |
|---|---|---|---|---|---|
| Citrate | Phosphofructokinase 1 | Negative allosteric | 0.1-2.0 | 0.5 | Glycolysis regulation |
| Alpha-ketoglutarate | Isocitrate dehydrogenase | Substrate availability | 0.05-0.5 | 0.2 | TCA cycle flux control |
| Succinate | Succinate dehydrogenase | Product inhibition | 0.2-1.5 | 1.0 | Electron transport coupling |
| Fumarate | Fumarase | Equilibrium shift | 0.1-1.0 | 0.8 | Metabolic equilibrium |
| Malate | Malate dehydrogenase | Coenzyme regulation | 0.3-2.0 | 1.5 | Redox balance |
| Oxaloacetate | Citrate synthase | Substrate inhibition | 0.05-0.3 | 0.1 | Cycle initiation control |
Redox Regulation and TCA Cycle Control
The TCA cycle exhibits tight regulation through redox-sensitive mechanisms. NADH accumulation inhibits multiple TCA cycle enzymes including pyruvate dehydrogenase, isocitrate dehydrogenase, and alpha-ketoglutarate dehydrogenase [11]. This coordinated inhibition prevents excessive NADH production when electron transport chain capacity is saturated.
Acetyl-CoA levels regulate pyruvate dehydrogenase activity through product inhibition, while also activating pyruvate carboxylase to increase oxaloacetate synthesis [11]. This reciprocal regulation maintains balanced substrate availability for TCA cycle initiation.
Chiral Recognition in Membrane Transport Proteins
Membrane transport proteins demonstrate sophisticated chiral recognition mechanisms that enable enantioselective substrate transport across biological membranes [14] [15]. These recognition systems represent evolutionary adaptations that allow cells to discriminate between stereoisomers based on their three-dimensional molecular architecture [16] [17].
Molecular Mechanisms of Chiral Recognition
Chiral recognition in membrane transport proteins operates through multiple molecular mechanisms, with the three-point interaction model serving as the fundamental paradigm [18]. This model requires simultaneous interaction between three complementary binding sites on the transport protein and three corresponding sites on the chiral substrate [18].
Organic cation transporters (OCTs) demonstrate variable degrees of stereoselectivity depending on the specific transporter subtype and substrate characteristics [14] [15]. OCT1 exhibits minimal stereoselectivity for most substrates, while OCT2 shows moderate to high stereoselectivity for specific compounds [14]. OCT3 displays the highest degree of stereoselectivity, with some substrates showing up to 25-fold preference for specific enantiomers [14].
The molecular basis for chiral recognition involves specific amino acid residues within the transport protein that create asymmetric binding environments. Hydrogen bonding, electrostatic interactions, and steric hindrance contribute to enantiomeric discrimination [19] [18]. The binding pocket architecture determines which enantiomer can achieve optimal complementarity with the protein surface.
Enantioselective Transport Mechanisms
Amino acid transporters demonstrate particularly sophisticated chiral recognition capabilities, reflecting the biological necessity for L-amino acid selectivity [20] [21]. These transporters utilize multiple recognition elements including carboxyl group positioning, amino group orientation, and side chain accommodation [20].
Peptide transporters show enantioselective recognition patterns that depend on the stereochemical configuration of constituent amino acids [17]. The transport efficiency varies significantly between diastereomers, with specific preferences for particular stereochemical combinations [17].
Artificial membrane channels have been developed to study chiral recognition mechanisms, revealing that channel geometry and chemical functionality determine enantiomeric selectivity [20] [21]. These studies demonstrate that chiral recognition is achievable through synthetic systems that mimic biological recognition elements.
Structural Determinants of Stereoselectivity
The structural determinants of chiral recognition in membrane transport proteins involve specific binding pocket features that create enantioselective environments [22]. Molecular size and hydrogen bonding capability of substrates significantly influence their chiral recognition by transport proteins [22].
Electrostatic asymmetry within transport proteins creates directional preferences that favor specific enantiomers [23]. The distribution of charged residues generates asymmetric electric fields that orient chiral substrates in preferred conformations [23].
Binding affinity differences between enantiomers result from differential complementarity between substrate and protein binding sites [14]. These differences manifest as altered Km values, with preferred enantiomers showing enhanced binding affinity and transport efficiency.
| Transport Protein | Chiral Recognition Site | Stereoselectivity Factor | Molecular Mechanism | Kinetic Parameter (Km ratio) | Preferred Enantiomer |
|---|---|---|---|---|---|
| Organic Cation Transporter 1 | Binding pocket | 1.5-4.0 | Three-point interaction | 2.1 | R-form |
| Organic Cation Transporter 2 | Allosteric site | 2.0-37.0 | Hydrogen bonding | 5.8 | S-form |
| Amino Acid Transporter | Substrate channel | 2.0-25.0 | Steric hindrance | 12.5 | L-form |
| Peptide Transporter 1 | Recognition domain | 1.2-3.0 | Electrostatic interaction | 1.8 | D-form |
| Monoamine Transporter | Binding cleft | 1.5-5.0 | Hydrophobic interaction | 3.2 | R-form |
Physiological Implications of Chiral Transport
Enantioselective transport has profound physiological implications for drug disposition and metabolism [15] [24]. The preferential transport of specific enantiomers can lead to differential tissue distribution and therapeutic efficacy [15]. Understanding these mechanisms is crucial for pharmaceutical development and personalized medicine approaches.
Membrane chirality itself contributes to enantioselective permeation, with chiral phospholipid headgroups creating asymmetric membrane environments [17]. These findings suggest that membrane composition influences drug transport and distribution in ways that extend beyond specific transporter interactions.