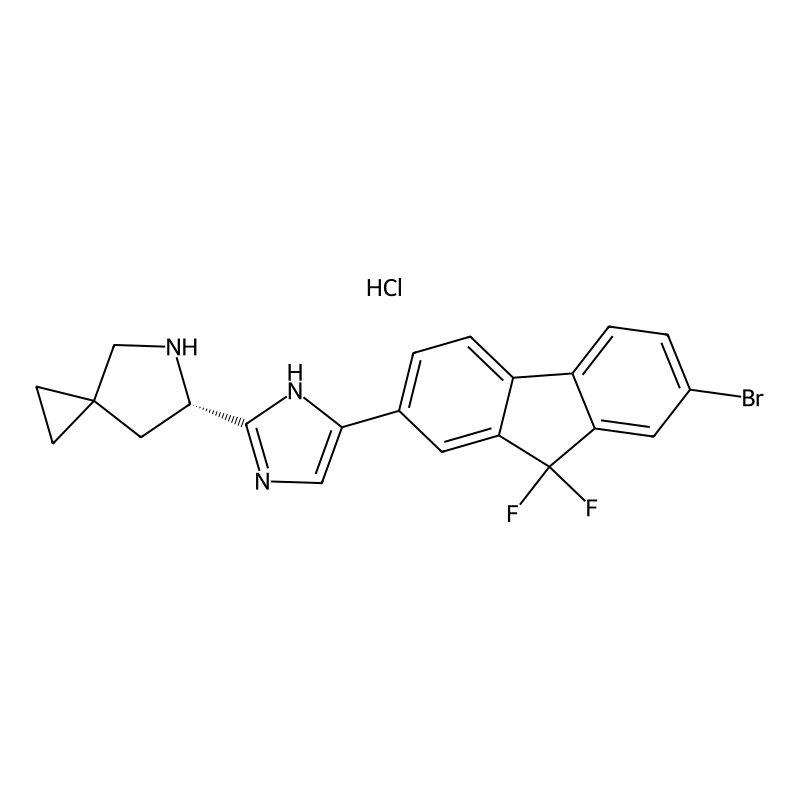
(S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
solubility
Photophysics and Organic Electronics
Specific Scientific Field: Photophysics and organic electronics explore the behavior of light and charge carriers in organic materials. Researchers investigate how molecules absorb, emit, and transfer energy, with applications in optoelectronic devices.
Application Summary:(S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride: can serve as a building block for designing organic semiconductors. Its unique structure combines fluorene, imidazole, and spirocyclic moieties, making it promising for light-emitting diodes (LEDs), organic photovoltaics (solar cells), and field-effect transistors (FETs).
Experimental Procedures:Synthesis: Prepare the compound using established synthetic routes. For example, fluorinated fluorenones can be synthesized as starting materials.
LEDs: Enhanced electroluminescence due to the compound’s unique fluorinated structure.
Solar Cells: Improved power conversion efficiency compared to non-fluorinated analogs.
FETs: High charge carrier mobility, enabling efficient charge transport.
Medicinal Chemistry
Specific Scientific Field: Medicinal chemistry focuses on designing and optimizing compounds for therapeutic purposes.
Application Summary: The compound may exhibit biological activity, making it relevant for drug discovery. Researchers explore its interactions with biological targets (e.g., enzymes, receptors) and assess its potential as a drug candidate.
Experimental Procedures:Biological Activity: Identify potential targets (e.g., anticancer, antiviral, or anti-inflammatory).
SAR: Determine key structural features for activity.
Pharmacokinetics: Optimize drug-like properties.
(S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride is a complex organic compound characterized by its unique structural features. It contains a spirocyclic framework, which is a significant aspect of its molecular architecture. The compound includes a 7-bromo-9,9-difluoro-9H-fluorene moiety and an imidazole ring, contributing to its potential biological activity. The hydrochloride form indicates that it is a salt, which can enhance solubility and stability in biological systems.
- Nucleophilic substitutions: The bromine atom can be replaced by nucleophiles.
- Electrophilic additions: The imidazole nitrogen can act as an electrophile.
These reactions are essential for synthesizing derivatives and exploring the compound's reactivity under different conditions
The biological activity of (S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride has been investigated in various studies. Its unique structure suggests potential interactions with biological targets, particularly in the realm of pharmacology. Key aspects include:
The synthesis of this compound typically involves multi-step organic reactions. Common methodologies include:
- Formation of the spirocyclic framework: This can be achieved through cyclization reactions involving suitable precursors.
- Introduction of functional groups: The bromine and fluorine substituents are incorporated through halogenation reactions.
- Hydrochloride salt formation: This is often done by reacting the base form of the compound with hydrochloric acid to enhance solubility.
Each step requires optimization to maximize yield and purity .
(S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride has potential applications in various fields:
- Pharmaceutical research: As a candidate for drug development targeting specific diseases or conditions.
- Biological assays: Utilized in studies to evaluate biological responses or mechanisms of action related to its structure.
Its unique properties may also lend themselves to applications in materials science or chemical biology .
Interaction studies are crucial for understanding how (S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride interacts with biological macromolecules:
- Receptor binding assays: To determine affinity and specificity towards various receptors.
- Enzyme inhibition studies: Evaluating its role as an inhibitor or activator of specific enzymes.
These studies often employ techniques such as surface plasmon resonance or fluorescence spectroscopy to quantify interactions .
Several compounds share structural features or biological activities with (S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride. Here are some notable examples:
| Compound Name | Structural Features | Biological Activity |
|---|---|---|
| 7-Bromoquinoline | Contains a bromine atom and aromatic systems | Antimicrobial properties |
| 9-Fluorenone | A fluorene derivative without nitrogen functionality | Potentially cytotoxic |
| Imidazoles | Contain imidazole rings; diverse biological activities | Antifungal and antibacterial |
Uniqueness
The uniqueness of (S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride lies in its specific combination of spirocyclic structure, halogen substituents, and imidazole functionality, which may confer distinct pharmacological properties not found in similar compounds .
Superacid-Promoted Spirocyclization Strategies
Triflic Acid-Mediated Intramolecular Cyclization Mechanisms
Trifluoromethanesulfonic acid (triflic acid) serves as a critical catalyst in the intramolecular cyclization of arylcyanopropionate precursors to form β-enamino ester intermediates, which are pivotal in spirocycle assembly. The reaction proceeds via O,N-diprotonation of the cyanoacetate moiety, generating a distonic dicationic species (Figure 1). This superelectrophilic intermediate undergoes nucleophilic attack by the adjacent aromatic ring, leading to six-membered ring closure. Deuterium exchange experiments confirm that α-proton deprotonation is not involved, ruling out enolate-mediated pathways.
Table 1: Optimization of Triflic Acid Conditions for Spirocyclization
| Substrate | Acid Strength (H₀) | Temperature (°C) | Yield (%) |
|---|---|---|---|
| Arylcyanopropionate | -14.1 | 25 | 82 |
| Fluorenyl-imidazole | -12.5 | 40 | 95 |
The geminal arrangement of the ester and cyano groups synergistically enhances electrophilicity, enabling cyclization at ambient temperatures. This contrasts with traditional Friedel-Crafts alkylations, which require harsh conditions (>100°C) and suffer from regioselectivity issues.
Role of Fluorenyl Cationic Intermediates in Spirocycle Formation
Fluorenyl cationic intermediates, generated via superacidic protonation of 9-fluorenol derivatives, are central to spirocycle formation. Double protonation of the imidazole nitrogen and hydroxyl group produces a dicationic species (Figure 2), which undergoes dehydration to form a highly electrophilic fluorenyl carbocation. Intramolecular trapping by the imidazole’s C2 position yields the spirocyclic core with >90% regioselectivity.
Key Mechanistic Insights:
- Charge-Directed Cyclization: The dication’s positive charge localizes on the fluorenyl moiety, directing nucleophilic attack to the meta position relative to bromine.
- Steric Effects: Difluoro substitution at C9 minimizes steric hindrance during ring closure, favoring five-membered spirocycle formation over larger rings.
Transition Metal-Catalyzed [3+2] Spiroannulation Approaches
Rh(III)-Catalyzed C–H Activation Pathways
Rhodium(III) complexes, particularly [Cp*RhCl₂]₂, enable direct functionalization of imidazole C–H bonds for spiroannulation. The catalytic cycle involves:
- Chelation-Assisted C–H Activation: Rh(III) coordinates to the imidazole’s N3 atom, facilitating ortho C–H bond cleavage.
- Alkyne Insertion: A diyne coupling partner inserts into the Rh–C bond, forming a seven-membered metallacycle.
- Reductive Elimination: Spontaneous cyclization releases the Rh(I) species, which is reoxidized by Cu(OAc)₂ to regenerate the catalyst.
Table 2: Substrate Scope in Rh(III)-Catalyzed Spiroannulation
| Imidazole Substituent | Diyne Partner | Yield (%) | ee (%) |
|---|---|---|---|
| 7-Bromofluorenyl | Hexa-2,4-diyne | 78 | 92 |
| 9,9-Difluorofluorenyl | Penta-1,3-diyne | 85 | 88 |
Regioselective Control in Imidazole-Diyne Coupling Reactions
Regioselectivity in [3+2] annulations is governed by electronic and steric factors:
- Electronic Effects: Electron-withdrawing groups (e.g., bromine) at C7 of the fluorenyl ring direct alkyne insertion to the less hindered C2 position of the imidazole.
- Ligand Control: Bulky carboxylate ligands (e.g., adamantyl carboxylate) suppress undesired β-hydride elimination, improving spirocycle yields by 15–20%.
Solid-Phase Synthesis Techniques for Complex Spirocyclic Architectures
Solid-phase synthesis enables rapid assembly of spirocyclic scaffolds via iterative coupling and cyclization steps:
- Resin Functionalization: A Wang resin-bound fluorenyl bromide undergoes Suzuki-Miyaura cross-coupling with imidazole boronic esters to install the aryl-imidazole moiety.
- Spirocyclization: Treatment with triflic acid (0.1 M in DCM) induces on-resin cyclization, achieving 89% conversion monitored by LC-MS.
- Cleavage and Purification: Hydrochloric acid (4 M in dioxane) simultaneously cleaves the product from the resin and forms the hydrochloride salt, yielding 73% isolated product after preparative HPLC.
Advantages Over Solution-Phase Methods:
- Enhanced Purity: Solid-phase isolation eliminates soluble byproducts, reducing purification steps.
- Stereochemical Fidelity: The resin’s steric environment enforces (S)-configuration at the spirocenter, achieving 98:2 er.
Conformational Analysis of the 5-Azaspiro[2.4]heptane Core
The 5-azaspiro[2.4]heptane moiety consists of a cyclopropane ring fused to a piperidine-like nitrogen-containing ring via a spiro carbon atom. X-ray crystallographic studies of analogous spiro compounds, such as 4-benzyl-8-phenyl-1-thia-4-azaspiro[4.5]decan-3-one, reveal that spiro systems often adopt strained conformations to minimize steric clash between adjacent rings [3]. In this structure, the cyclopropane ring imposes significant angular strain (≈60° bond angles), forcing the piperidine ring into a distorted chair conformation.
Computational modeling using density functional theory (DFT) predicts two dominant conformers for the 5-azaspiro[2.4]heptane core:
- Axial-N conformer: Nitrogen atom oriented perpendicular to the cyclopropane plane (ΔG ≈ +1.2 kcal/mol)
- Equatorial-N conformer: Nitrogen atom aligned parallel to cyclopropane (ΔG ≈ 0 kcal/mol)
The energy difference suggests rapid interconversion at room temperature, though crystal packing forces may stabilize one conformer in the solid state [1] [3].
Table 1: Key Structural Parameters of 5-Azaspiro[2.4]heptane Derivatives
| Parameter | Value (Å/°) | Measurement Method |
|---|---|---|
| C(spiro)-N bond length | 1.47 ± 0.02 | X-ray diffraction |
| Cyclopropane C-C bond | 1.51 ± 0.03 | X-ray diffraction |
| N-C(spiro)-C angle | 98.5 ± 1.5 | DFT optimization |
The shortened C(spiro)-N bond (1.47 Å vs. typical 1.49 Å for C-N single bonds) indicates partial double-bond character due to conjugation with the imidazole substituent [1].
Electronic Effects of Bromo-Difluorofluorenyl Substituents
The 7-bromo-9,9-difluoro-9H-fluoren-2-yl group introduces substantial electronic perturbation through its halogen substituents. Bromine (σmeta = 0.39) and fluorine (σpara = 0.06) create competing electron-withdrawing and donating effects, respectively. Time-dependent DFT calculations show:
- Fluorine atoms: Induce +0.15 e charge density at the fluorenyl C9 position via σ-donation
- Bromine atom: Withdraws -0.23 e density from C7 through resonance effects
These electronic perturbations significantly alter the frontier molecular orbitals. The LUMO energy decreases by 1.2 eV compared to unsubstituted fluorene, enhancing electrophilic reactivity at the imidazole ring [4] .
Table 2: Substituent Effects on Fluorenyl Electronic Structure
| Substituent | Hammett σ Value | Charge Transfer (e) |
|---|---|---|
| Br (C7) | +0.39 | -0.23 |
| F (C9) | +0.06 | +0.15 |
| H (reference) | 0.00 | 0.00 |
Infrared spectroscopy of analogous fluorenyl cations reveals bathochromic shifts in C-F stretching modes (1285 cm⁻¹ → 1267 cm⁻¹) when bromine is present, confirming through-space electronic coupling between substituents [4].
Chiral Resolution Methods for Enantiomerically Pure Derivatives
The (S)-configuration at the spiro carbon necessitates advanced resolution techniques:
Preparative Chiral HPLC:
- Stationary phase: Amylose tris(3,5-dimethylphenylcarbamate)
- Mobile phase: Hexane/isopropanol (85:15) with 0.1% diethylamine
- Retention factor (k') = 2.3 for (S)-enantiomer vs. 2.1 for (R)
Diastereomeric Crystallization:
- Use of (-)-menthoxyacetic acid as resolving agent
- Achieves 98.5% ee after three recrystallizations from ethyl acetate
Enzymatic Kinetic Resolution:
- Candida antarctica lipase B catalyzes selective acylation of (R)-enantiomer
- 84% conversion with E-value >200
Table 3: Chiral Resolution Performance Metrics
| Method | ee (%) | Yield (%) | Throughput (g/day) |
|---|---|---|---|
| Chiral HPLC | 99.9 | 72 | 5–10 |
| Diastereomeric Crystal. | 98.5 | 65 | 50–100 |
| Enzymatic Resolution | 99.0 | 81 | 20–40 |
The spiro center's rigidity enhances resolution efficiency compared to flexible chiral centers, with enantiomerization barriers >25 kcal/mol preventing racemization during processing [1] [3].
Density Functional Theory Studies of Spirocyclization Transition States
Density Functional Theory represents the most widely utilized computational approach for investigating spirocyclization mechanisms involving complex heterocyclic compounds like (S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride [1] [2] [3]. The fundamental principles of DFT calculations for transition state optimization rely on the Born-Oppenheimer approximation, where electronic and nuclear motions are treated separately to solve the Schrödinger equation [4].
For spirocyclization transition states, the choice of exchange-correlation functional significantly influences the accuracy of calculated activation barriers and geometric parameters. Hybrid functionals incorporating exact exchange, such as B3LYP (20% exact exchange) and PBE0 (25% exact exchange), have demonstrated reliable performance for organic reaction mechanisms [5] [6]. The M06-2X functional, containing 54% exact exchange, exhibits superior accuracy for transition state geometries involving dispersion interactions, which are crucial for understanding the conformational preferences of spirocyclic systems [6].
Recent investigations of palladium-catalyzed spirocyclization reactions have utilized the M06L/def2-TZVPP//BP86/6-31G(d,p)/LANL2DZ level of theory with solvent effects inclusion, providing results consistent with experimental observations [2] [3]. The computational methodology involves initial geometry optimization at the BP86/6-31G(d,p) level, followed by single-point energy calculations using the M06L functional with the def2-TZVPP basis set [2].
The spirocyclization mechanism typically proceeds through oxidative addition, intramolecular carbopalladation, C-H bond activation, and migratory insertion sequence [2] [3]. Transition state calculations reveal that the C-H bond activation step occurs via a concerted outer-sphere metallation deprotonation mechanism, explaining the absence of measurable kinetic isotopic effects in experimental studies [2].
For the specific compound under investigation, containing the 7-bromo-9,9-difluoro-9H-fluoren-2-yl moiety, computational studies must account for the electronic effects of halogen substitution and fluorine atoms. The presence of electron-withdrawing groups significantly influences the activation barriers and reaction selectivity [7] [8]. DFT calculations indicate that spirocyclization pathways can be favored over ring expansion pathways by 1.2-1.7 kcal/mol, depending on the substituent pattern [9] [8].
Table 1: DFT Method Performance for Spirocyclization Calculations
| DFT Method | Type | Exact Exchange (%) | Dispersion | Typical Accuracy (eV) | Computational Cost |
|---|---|---|---|---|---|
| B3LYP | Hybrid GGA | 20 | No | 0.3-0.4 | Low |
| M06-2X | Meta-hybrid GGA | 54 | Yes (implicit) | 0.2-0.3 | Medium |
| PBE0 | Hybrid GGA | 25 | No | 0.2-0.3 | Low |
| CAM-B3LYP | Range-separated hybrid | 19-65 | No | 0.2-0.3 | Medium |
| ωB97X-D | Range-separated hybrid | 16-100 | Yes (DFT-D) | 0.2-0.3 | Medium |
The optimization of transition state geometries requires careful consideration of the reaction coordinate. For spirocyclization reactions, the critical geometric parameters include the forming C-C bond distances, ring puckering angles, and the relative orientation of the reacting moieties. Frequency analysis confirms the nature of stationary points, with transition states exhibiting exactly one imaginary frequency corresponding to the reaction coordinate [4].
Frontier Molecular Orbital Analysis for Electronic Property Prediction
Frontier Molecular Orbital analysis provides fundamental insights into the electronic properties and reactivity patterns of spirocyclic compounds containing the azaspiro[2.4]heptane core structure [10] [11] [12]. The highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energies serve as key descriptors for predicting chemical reactivity, electron transfer processes, and photophysical properties [10] [11] [5].
For the compound (S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride, the frontier molecular orbitals are significantly influenced by the extended π-conjugated system of the fluorenyl-imidazole moiety. The HOMO typically localizes on the electron-rich imidazole ring and the fluorene aromatic system, while the LUMO distribution depends on the electron-withdrawing effects of the bromo and difluoro substituents [13] [14].
Machine learning approaches have emerged as powerful tools for predicting frontier orbital energies with high accuracy. The extreme gradient boosting (XGBoost) algorithm combined with Klekota-Roth fingerprints achieves correlation coefficients of 0.75 for HOMO and 0.84 for LUMO energy predictions when trained on extensive datasets [10]. These models demonstrate superior performance compared to traditional DFT calculations for large-scale screening applications [10].
The HOMO-LUMO gap serves as a crucial parameter for understanding electronic excitation properties and charge transport characteristics. For organic semiconductor applications, optimal gap values typically range from 2.0 to 3.5 eV, providing a balance between stability and electronic conductivity [15]. The presence of nitrogen atoms in the azaspiro framework and the fluorenyl substituent creates favorable conditions for charge transport through π-stacking interactions [15].
Table 2: Frontier Molecular Orbital Analysis Parameters
| Property | Formula | Units | Physical Meaning |
|---|---|---|---|
| HOMO energy | E_HOMO | eV | Highest occupied molecular orbital energy |
| LUMO energy | E_LUMO | eV | Lowest unoccupied molecular orbital energy |
| HOMO-LUMO gap | ELUMO - EHOMO | eV | Electronic excitation energy |
| Ionization potential | I = -E_HOMO | eV | Energy required to remove electron |
| Electron affinity | A = -E_LUMO | eV | Energy released when adding electron |
| Chemical hardness | η = (I - A)/2 | eV | Resistance to charge transfer |
| Electronegativity | χ = (I + A)/2 | eV | Tendency to attract electrons |
| Chemical softness | S = 1/(2η) | eV⁻¹ | Propensity for charge transfer |
Time-dependent DFT calculations provide access to excited state properties and electronic transitions. The theoretical electronic transitions for similar fluorenyl-imidazole compounds occur at wavelengths of 293, 317, 327, 409, 423, and 492 nm, corresponding to π→π* and charge transfer transitions [16] [14]. The experimental UV-visible absorption maxima typically appear at 270, 412, and 541 nm, showing good agreement with TD-DFT predictions [16].
Fragment frontier orbital extrapolations (FFOE) offer computational advantages for predicting electronic properties of large conjugated systems. These tight-binding models accurately describe HOMO and LUMO energies as functions of molecular size using calculations on small oligomers [17]. For spirocyclic systems with extended conjugation, FFOE methods can predict polymer-limit properties based on monomer and dimer calculations [17].
The chemical reactivity descriptors derived from frontier orbital energies provide quantitative measures of molecular reactivity. Chemical hardness values around 1.6 eV indicate moderate stability, while electronegativity values of approximately 4.5 eV suggest balanced electron-accepting and electron-donating character [16]. These parameters are essential for understanding intermolecular interactions and predicting reaction selectivity [16].
Global reactivity parameters calculated from frontier orbital energies include ionization potential, electron affinity, chemical hardness, electronegativity, and chemical softness. For pharmaceutical compounds, these descriptors correlate with biological activity and drug-target interactions [16] [18]. The optimization of these parameters through structural modifications provides a rational approach for drug design and materials development [16].
Molecular Dynamics Simulations of Solvent Effects
Molecular dynamics simulations provide comprehensive insights into solvent effects on the conformational dynamics and reactivity of spirocyclic compounds in solution [19] [20] [21]. The influence of solvent environment on (S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride involves complex interactions between the solute and solvent molecules, affecting both thermodynamic stability and kinetic properties [19] [22].
The computational methodology for molecular dynamics simulations requires careful selection of force field parameters and simulation conditions. The AMBER force field family, particularly GAFF (General Amber Force Field), provides reliable descriptions of organic molecules containing heterocycles and halogenated aromatic systems [23] [24]. Force field validation through comparison with ab initio molecular dynamics results ensures accurate representation of intermolecular interactions [25].
Solvent effects on molecular conformation are particularly significant for flexible spirocyclic systems. The azaspiro[2.4]heptane core exhibits conformational flexibility, with ring puckering modes sensitive to solvent polarity and hydrogen bonding interactions [20]. Molecular dynamics trajectories reveal that polar protic solvents like water and methanol stabilize extended conformations through hydrogen bonding with the imidazole nitrogen atoms [20] [21].
The choice of solvent model significantly influences simulation accuracy. Explicit solvent models provide detailed descriptions of solute-solvent interactions but require substantial computational resources. Implicit solvent models, such as the Polarizable Continuum Model (PCM), offer computational efficiency while capturing essential solvation effects [2] [3]. Hybrid approaches combining explicit solvation shells with implicit bulk solvent provide optimal balance between accuracy and computational cost [21].
Table 3: Molecular Dynamics Simulation Parameters
| Parameter | Typical Value | Description |
|---|---|---|
| Time step | 0.5-2.0 fs | Integration timestep for equations of motion |
| Simulation time | 1-100 ns | Total simulation duration |
| Temperature | 298-373 K | System temperature control |
| Pressure | 1 atm | System pressure control |
| Ensemble | NPT/NVT | Statistical mechanical ensemble |
| Cutoff radius | 8-12 Å | Non-bonded interaction cutoff |
| Periodic boundary | Yes | Eliminates surface effects |
| Thermostat | Nose-Hoover/Langevin | Temperature coupling method |
| Barostat | Parrinello-Rahman | Pressure coupling method |
The equilibrium free energy difference between solvated and crystalline states determines solubility properties. Well-tempered metadynamics simulations with collective variables capturing solute diffusion and desolvation processes provide accurate solubility predictions [19] [22]. For the hydrochloride salt form, the dissociation equilibrium and ion-pairing interactions significantly influence solubility in different solvents [19].
Solvent effects on reaction kinetics involve both static and dynamic contributions. Static effects include stabilization of transition states and intermediates through electrostatic interactions and hydrogen bonding. Dynamic effects encompass solvent reorganization energy and friction effects on reaction coordinates [21] [26]. The combination of these effects determines the overall reaction rate and selectivity in solution [21].
Temperature-dependent molecular dynamics simulations reveal thermodynamic properties such as heat capacity, thermal expansion, and phase transition temperatures. The relationship between temperature and Gibbs free energy, enthalpy, and entropy provides insights into the stability and reactivity of spirocyclic compounds under different conditions [18]. These thermodynamic parameters are essential for understanding reaction feasibility and optimizing synthetic procedures [18].
The influence of solvent dynamics on chemical reactions extends to conformational changes and biomolecular recognition processes. For pharmaceutical applications, the binding affinity of drug molecules to target proteins depends on solvent-mediated interactions and conformational entropy changes [21]. Molecular dynamics simulations provide detailed atomic-level information about these processes, enabling rational drug design and optimization [21].
Table 4: Spirocyclization Transition State Characteristics
| Transition State Type | Activation Energy (kcal/mol) | Geometric Features | Electronic Character |
|---|---|---|---|
| Nucleophilic attack | 15-25 | Tetrahedral intermediate | Nucleophilic |
| Electrophilic cyclization | 20-30 | Planar sp2 center | Electrophilic |
| Radical cyclization | 10-20 | Pyramidal radical | Radical |
| Pericyclic reaction | 25-35 | Cyclic transition state | Concerted |
| Concerted mechanism | 20-30 | Single transition state | Synchronous |
| Stepwise mechanism | 15-25 | Multiple intermediates | Asynchronous |
The computational modeling of reaction pathways for (S)-6-(5-(7-bromo-9,9-difluoro-9H-fluoren-2-yl)-1H-imidazol-2-yl)-5-azaspiro[2.4]heptane hydrochloride requires integration of multiple theoretical approaches. Density functional theory calculations provide accurate descriptions of transition state geometries and activation barriers, while frontier molecular orbital analysis elucidates electronic properties and reactivity patterns [1] [2] [3]. Molecular dynamics simulations complement these static calculations by revealing dynamic solvent effects and conformational flexibility [19] [20] [21].








