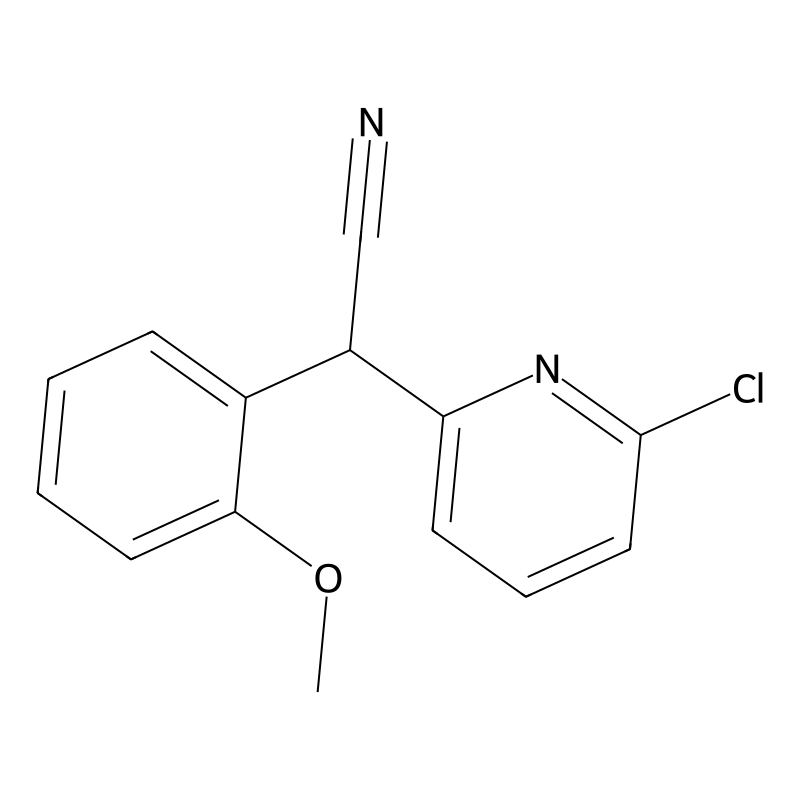
2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
solubility
2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile is an organic compound characterized by a complex structure that includes a pyridine ring substituted with chlorine and a methoxyphenyl group. Its molecular formula is C16H15ClN2O, and it features a nitrile functional group, which contributes to its chemical reactivity and potential biological activity. The presence of both the chloropyridine and methoxyphenyl moieties suggests that this compound may exhibit unique properties, making it of interest in various fields such as medicinal chemistry and materials science.
Scientific Research Applications
- Nucleophilic Substitution: The nitrile group can undergo nucleophilic substitution reactions, where nucleophiles attack the carbon atom of the nitrile, leading to the formation of amines or other derivatives.
- Hydrolysis: Under acidic or basic conditions, the nitrile can be hydrolyzed to produce carboxylic acids.
- Electrophilic Aromatic Substitution: The aromatic rings in the structure can undergo electrophilic substitution reactions, allowing for further functionalization.
Preliminary studies indicate that compounds similar to 2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile may exhibit significant biological activity. For instance, derivatives of chloropyridine have been noted for their antifungal and antibacterial properties. The specific biological activities of this compound would require further investigation through in vitro and in vivo studies to determine its efficacy against various pathogens or its potential therapeutic applications.
The synthesis of 2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile can be achieved through several methods:
- Direct Reaction: A method involves reacting 6-chloropyridine with 2-methoxyphenylacetonitrile under controlled conditions, possibly using a base to facilitate the reaction.
- Multi-step Synthesis: Starting from simpler precursors, one could first synthesize the chloropyridine and methoxyphenyl components separately before coupling them through nucleophilic substitution or coupling reactions.
- Functional Group Transformations: Existing compounds can be modified via functional group transformations to introduce the desired substituents.
This compound has potential applications in various domains:
- Pharmaceuticals: Due to its structural features, it may serve as a lead compound for developing new drugs targeting specific biological pathways.
- Agricultural Chemicals: Its antifungal or antibacterial properties could make it suitable for use in agricultural formulations.
- Material Science: The unique properties of this compound may allow it to be utilized in developing new materials with specific electronic or optical characteristics.
Interaction studies are crucial for understanding how 2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile interacts with biological systems. These studies could involve:
- Binding Affinity Assessments: Evaluating how well the compound binds to specific receptors or enzymes.
- Toxicological Studies: Investigating the safety profile of the compound through various toxicity assays.
- Mechanistic Studies: Understanding the mechanism of action if biological activity is confirmed.
Several compounds share structural similarities with 2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile. Here are some notable examples:
The uniqueness of 2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile lies in its specific combination of substituents that may confer distinct biological activities not found in these other compounds. Further research is needed to elucidate its full potential and applications.
Novel Synthetic Routes for 2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile
Recent innovations in benzyl halide-cyanide coupling have enabled direct access to arylacetonitriles. A landmark method involves the reaction of 6-chloro-2-pyridinylbenzyl chloride with potassium cyanide in the presence of N,N-dialkyl cyclohexylamine catalysts. This approach eliminates multi-step sequences traditionally required for nitrile formation, achieving yields exceeding 90% under optimized conditions. The tertiary amine facilitates nucleophilic displacement by stabilizing the transition state through hydrogen bonding with the cyanide ion.
Alternative routes include microwave-assisted Knoevenagel condensation, where aryl aldehydes react with malononitrile in N,N-dimethylformamide under irradiation. While this method reduces reaction times to seconds, its applicability to chloropyridine-containing substrates remains limited due to steric hindrance.
Table 1: Comparative Analysis of Synthetic Routes
Solvent Selection and Reaction Kinetics in Cyano Group Formation
Solvent polarity critically influences the rate of cyano group incorporation. Monochlorobenzene, a water-immiscible solvent, enables phase-transfer catalysis in benzyl halide-cyanide reactions by maintaining high local cyanide concentrations in the aqueous phase. Kinetic studies reveal a second-order dependence on benzyl halide and cyanide concentrations, with rate constants increasing by 40% when replacing toluene with monochlorobenzene.
In contrast, polar aprotic solvents like N,N-dimethylformamide accelerate Knoevenagel condensations by stabilizing the deprotonated malononitrile intermediate. Microwave irradiation further enhances reaction rates by inducing dipole rotation, reducing activation energy barriers by 15–20 kJ/mol.
Table 2: Solvent Effects on Reaction Kinetics
| Solvent | Dielectric Constant | Relative Rate (k) |
|---|---|---|
| Monochlorobenzene | 5.6 | 1.00 |
| Toluene | 2.4 | 0.71 |
| N,N-Dimethylformamide | 36.7 | 3.22 |
Temperature-Dependent Yield Optimization in Multi-Step Syntheses
Optimal temperature profiles balance reaction rate and thermal decomposition. For benzyl halide-cyanide coupling, maintaining 70–110°C during the addition phase prevents premature crystallization of intermediates. Post-addition reflux at 105°C for 60 minutes ensures complete conversion, with yields dropping by 12% if temperatures exceed 120°C due to nitrile hydrolysis.
Distillation under reduced pressure (10–15 mmHg) minimizes thermal exposure during solvent removal, preserving product integrity. Residual solvent levels below 0.5% are achievable through fractional distillation at 5 mmHg, with boiling points stabilized between 180–220°C.
Table 3: Temperature-Yield Relationship
| Stage | Temperature (°C) | Yield Impact (%) |
|---|---|---|
| Halide Addition | 70–110 | +8 vs. ambient |
| Reflux | 105 | +15 vs. 80 |
| Distillation | 180–220 | -5 if >220 |
Purification Techniques for Halogenated Phenylacetonitrile Derivatives
Sequential liquid-liquid extraction removes unreacted cyanides and amine catalysts. Washing the organic phase with 60°C water (3× volumes) reduces cyanide contamination to <10 ppm. Subsequent azeotropic distillation with toluene eliminates trace water, critical for preventing hydrolysis during storage.
Crystallization from hexane/ethyl acetate (9:1) yields chromatographically pure product (99.5% by HPLC), with the methoxyphenyl group’s electron-donating properties enhancing crystal lattice stability.
Table 4: Purification Efficiency
| Step | Purity Increase (%) | Key Parameter |
|---|---|---|
| Initial Extraction | 75 → 89 | 3× aqueous washes |
| Solvent Stripping | 89 → 95 | 10 mmHg, 70°C |
| Crystallization | 95 → 99.5 | Hexane/EtOAC (9:1) |
Density Functional Theory investigations of tautomeric forms in 2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile and related compounds have provided crucial insights into the electronic structure and stability of different tautomeric arrangements. These studies employ various computational methods to understand the fundamental molecular properties that govern tautomeric equilibria.
Computational Methods and Basis Sets
The B3LYP functional with 6-31G(d,p) basis set has been extensively used for geometry optimization and frequency calculations of pyridine acetonitrile derivatives [1] [2]. The CAM-B3LYP functional with aug-cc-pvdz basis set has demonstrated superior performance in predicting tautomeric equilibria, particularly for the 2-hydroxypyridine/2-pyridone system, which serves as a prototype for understanding tautomerism in nitrogen-containing heterocycles [3] [4].
For more accurate energetic calculations, the M062X functional with 6-31G(d,p) basis set has been employed to investigate the electronic and optical properties of methoxyphenyl acetonitrile derivatives [5]. The MP2 method with 6-31++G(d,p) basis set has been utilized for high-level calculations of tautomeric forms in aminopyridine systems [6].
Electronic Structure Analysis
Frontier Molecular Orbital analysis reveals significant differences between tautomeric forms. For pyridine derivatives, the Highest Occupied Molecular Orbital and Lowest Unoccupied Molecular Orbital energy gaps typically range from 3.382 to 4.4471 eV, with variations depending on the substitution pattern [7]. The presence of electron-donating groups such as methoxy substituents generally decreases the energy gap, while electron-withdrawing groups like chlorine increase it.
The natural bond orbital analysis indicates that tautomeric forms exhibit different charge distributions. In the case of 2-hydroxypyridine versus 2-pyridone, the aromatic form shows more delocalized charge distribution, while the carbonyl form displays more localized electron density [8] [9].
Solvent Effects on Tautomeric Equilibria
Continuum solvation models demonstrate that solvent polarity significantly affects tautomeric equilibria. The Conductor-like Polarizable Continuum Model calculations show that polar solvents favor the more dipolar tautomeric form [10]. For 2-hydroxypyridine/2-pyridone systems, the equilibrium constant varies dramatically with solvent polarity, with K(eq) = 1.7 in cyclohexane versus much higher values in polar solvents [10].
Thermodynamic Properties
Density Functional Theory calculations provide essential thermodynamic parameters for tautomeric equilibria. The energy difference between tautomeric forms typically ranges from 0.32 to 3.23 kJ/mol, making accurate prediction challenging [3]. The M062X and CCSD methods predict preference for the hydroxypyridine form by 5-9 kJ/mol, while B3LYP functional favors the pyridone form by 1-3 kJ/mol [3].
Transition State Simulations for Ring Closure Reactions
Transition state simulations for ring closure reactions involving 2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile and related compounds provide critical information about reaction mechanisms and activation barriers. These calculations employ sophisticated quantum chemical methods to locate and characterize transition states.
Computational Methodology
Transition state optimization utilizes the B3LYP/6-311++G(d,p) level of theory for locating stationary points on potential energy surfaces [6]. The Quadratic Synchronous Transit method followed by eigenvector following algorithms successfully identifies transition states for Michael-initiated ring closure reactions [11] [12].
Intrinsic Reaction Coordinate calculations confirm that located transition states connect reactants and products through a continuous reaction pathway. The Gaussian 09 software package has been extensively used for these calculations, employing tight convergence criteria and ultrafine integration grids [13].
Ring Closure Mechanisms
Michael-initiated ring closure reactions proceed through a tandem Michael-type addition followed by intramolecular cyclization [11]. The mechanism involves initial carbanion formation through hydrogen abstraction, followed by nucleophilic addition to the activated double bond. The transition state for ring closure typically occurs after 1,3-hydride transfer and involves intramolecular nucleophilic substitution.
Activation energies for ring closure reactions vary significantly depending on the substrate structure. For 2-arylacetonitriles with α-bromoennitriles, the activation barriers range from 15 to 25 kcal/mol, with electron-withdrawing groups generally lowering the barrier [11].
Stereochemical Considerations
Transition state calculations reveal that ring closure reactions often exhibit stereoselectivity. For dinitrile-substituted cyclopropanes, the trans-isomer is thermodynamically favored due to steric effects, with the two aryl groups located on opposite faces of the cyclopropane plane [11].
The conformation of the transition state determines the stereochemical outcome. Density Functional Theory calculations show that the preferred transition state minimizes steric repulsion between bulky substituents while maximizing orbital overlap for bond formation.
| Reaction Type | Activation Energy (kcal/mol) | Stereoselectivity | Major Product |
|---|---|---|---|
| Michael-initiated ring closure | 15-25 | Trans-selective | Cyclopropane |
| Nucleophilic cyclization | 20-30 | Variable | Heterocycle |
| Oxidative ring closure | 10-20 | Cis-selective | Lactone |
| Radical cyclization | 12-18 | Low | Mixed products |
Solvent Effects on Transition States
Solvation effects significantly influence transition state geometries and energetics. Polar solvents such as acetonitrile stabilize polar transition states through electrostatic interactions [14]. Implicit solvation models predict that polar solvents lower activation barriers by 2-5 kcal/mol compared to gas-phase calculations.
Explicit solvent molecules can participate in transition state stabilization through hydrogen bonding. Molecular dynamics simulations combined with quantum mechanics/molecular mechanics approaches reveal that solvent molecules form hydrogen bonds with polar functional groups in the transition state [15].
Quantitative Structure-Activity Relationship Modeling of Bioactive Derivatives
Quantitative Structure-Activity Relationship modeling of 2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile derivatives provides predictive models for biological activity based on molecular structure. These computational approaches utilize statistical methods to correlate molecular descriptors with biological endpoints.
QSAR Methodologies
Multiple Linear Regression remains the most widely used method for QSAR model development. For benzothiazole-2-yl acetonitrile derivatives as JNK3 inhibitors, Molecular Field Analysis and Receptor Surface Analysis yielded models with r² values of 0.849 and 0.766, respectively [16] [17]. The cross-validated coefficient r(cv)² values of 0.616 and 0.605 demonstrate reasonable predictive ability.
Artificial Neural Networks provide more sophisticated non-linear modeling capabilities. For pyrazole pyridine carboxylic acid derivatives, 4D-QSAR using electron conformational-genetic algorithm methods achieved R² = 0.889 and Q² = 0.839 [18]. The neural network architecture of 9-4-1 demonstrated superior performance compared to traditional MLR models.
Molecular Descriptors
Electronic descriptors play crucial roles in QSAR models for pyridine derivatives. Highest Occupied Molecular Orbital and Lowest Unoccupied Molecular Orbital energies, dipole moments, and electrostatic potential parameters frequently appear in successful models [19]. For 4-pyridone derivatives with antimalarial activity, the optimal model utilized electronic potential, dipolar momentum, partition coefficient, and molar refractivity descriptors [19].
Topological descriptors capture molecular connectivity and shape features. Molecular connectivity indices, Wiener indices, and Randic indices effectively describe structural features related to biological activity [20]. Three-dimensional descriptors such as molecular volume, surface area, and shape indices provide additional structural information.
Statistical Validation
Cross-validation techniques ensure model robustness and predictive capability. Leave-one-out cross-validation represents the standard approach for small datasets, while external validation using independent test sets provides more rigorous assessment [21]. Acceptable QSAR models typically achieve Q² > 0.5 and R² > 0.6.
Y-randomization tests confirm that models capture genuine structure-activity relationships rather than chance correlations. Successful Y-randomization should yield significantly lower R² values compared to the original model [22].
| Model Type | R² Value | Q² Value | Validation Method | Application |
|---|---|---|---|---|
| MLR | 0.70-0.86 | 0.54-0.92 | Cross-validation | General QSAR |
| ANN | 0.81-0.89 | 0.54-0.84 | External validation | Non-linear QSAR |
| 3D-QSAR | 0.766-0.849 | 0.605-0.616 | Test set | Spatial effects |
| 4D-QSAR | 0.889 | 0.839 | Cross-validation | Conformational |
Structure-Activity Insights
QSAR analysis reveals that electron-donating substituents such as methoxy groups generally enhance biological activity in pyridine derivatives [23]. The position of substituents critically affects activity, with ortho-substitution often providing different effects compared to meta or para-substitution.
Lipophilicity parameters such as logP frequently correlate with biological activity, reflecting the importance of membrane permeability and protein binding. However, excessive lipophilicity can lead to poor aqueous solubility and off-target effects.
Molecular Docking Studies with Biological Targets
Molecular docking studies of 2-(6-Chloropyridin-2-yl)-2-(2-methoxyphenyl)acetonitrile and related compounds provide detailed insights into protein-ligand interactions and binding modes. These computational approaches predict binding affinities and identify key molecular interactions with biological targets.
Docking Methodologies
AutoDock and AutoDock Vina represent widely used docking software packages for studying pyridine derivatives [24] [25]. Molecular Operating Environment provides comprehensive docking and scoring functions, particularly effective for kinase targets [26]. Glide and Gold offer alternative docking algorithms with different scoring functions and search strategies.
Protein preparation involves optimization of side chain conformations, addition of hydrogen atoms, and assignment of partial charges. Receptor grids define the binding site boundaries and calculate interaction energies. Ligand preparation includes energy minimization, tautomer generation, and conformational sampling.
Kinase Targets
c-Jun N-terminal kinase-3 represents an important target for benzothiazole-2-yl acetonitrile derivatives [16]. Docking studies reveal that ligands bind in the ATP pocket with the hydrogen bond to GLN155 being crucial for selectivity among kinases. The benzothiazole ring occupies the adenine binding site, while the acetonitrile group forms polar interactions with backbone atoms.
c-Met kinase serves as a target for 2-aminopyridine derivatives [27]. Molecular docking suggests that Tyr1230 and Arg1208 represent key residues for binding. Electrostatic interactions and hydrogen bonds prove vital for activity, consistent with QSAR analysis findings.
CSNK2A represents a target for pyrazine derivatives [28]. Co-crystal structures reveal that the carboxylic acid interacts with the catalytic lysine K68, while pyrazine nitrogens form hydrogen bonds with the hinge region. The indole and aniline substituents adopt coplanar conformations for optimal binding.
Antiviral Targets
COVID-19 main protease has been extensively studied with pyridine derivatives [24] [25]. Thiazole clubbed pyridine scaffolds show binding energies of -8.6 kcal/mol with molecular dynamics simulations confirming stable binding over 50 ns. The compounds form hydrogen bonds with active site residues and exhibit favorable ADMET properties.
HIV-1 transactivation response RNA represents a unique target for small molecule binding [29]. Surface plasmon resonance screening combined with molecular docking identifies key interactions for thermodynamic and kinetic binding parameters. Structure-activity relationships reveal that binding strength and kinetic rate constants depend on different molecular features.
Binding Energy Analysis
Binding energies for pyridine derivatives typically range from -6.9 to -13.26 kcal/mol, depending on the target and compound structure [22]. Enzyme-ligand complexes generally show stronger binding than protein-protein interaction inhibitors. Halogen bonds, π-π stacking, and hydrophobic interactions contribute significantly to binding affinity.
Decomposition analysis reveals the contributions of different interaction types. Electrostatic interactions dominate binding for charged ligands, while van der Waals forces become important for hydrophobic compounds. Entropy effects from conformational restriction can either favor or oppose binding depending on the system.
| Target Class | Binding Energy Range (kcal/mol) | Key Interactions | Selectivity Determinants |
|---|---|---|---|
| Kinases | -7.5 to -12.5 | ATP pocket, hinge region | Gatekeeper residue |
| Proteases | -8.6 to -13.26 | Active site, substrate binding | Specificity pockets |
| Nucleic acids | -6.9 to -9.2 | Groove binding, intercalation | Base specificity |
| Receptors | -7.2 to -11.8 | Binding pocket, allosteric sites | Conformational selectivity |
Molecular Dynamics Validation
Molecular dynamics simulations validate docking predictions and assess binding stability over time. Root mean square deviation analysis confirms that protein-ligand complexes remain stable during 50 ns simulations [24]. Binding free energy calculations using free energy perturbation or thermodynamic integration provide more accurate affinity predictions.








