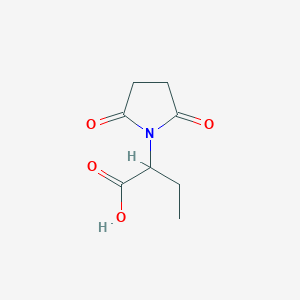
2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Solubility
Bioconjugation Agent:
Succinimidyl butanoic acid (SBA) functions as a versatile bioconjugation agent, facilitating the attachment of various biomolecules, such as antibodies, peptides, and drugs, to other molecules, including proteins, lipids, and nanoparticles. This attachment process allows researchers to create novel tools for targeted drug delivery, diagnostics, and bioimaging. The key advantage of SBA lies in its ability to react selectively with primary amines present in biomolecules under mild reaction conditions, minimizing potential side reactions and preserving biological activity.
Antibody-Drug Conjugates (ADCs):
SBA plays a crucial role in developing antibody-drug conjugates (ADCs), a class of targeted cancer therapies. These therapeutic agents utilize antibodies to specifically deliver cytotoxic drugs to cancer cells. SBA serves as a linker molecule, covalently connecting the antibody to the potent drug. This selective delivery approach minimizes drug exposure to healthy tissues, potentially reducing side effects compared to traditional chemotherapy.
Labeling of Biomolecules:
SBA also finds application in labeling various biomolecules for research purposes. By attaching fluorescent or radioactive tags to biomolecules using SBA, researchers can track their movement, localization, and interactions within cells or organisms. This labeling technique plays a vital role in studying cellular processes, protein-protein interactions, and drug targeting efficiency.
Biosensors and Biomaterials:
SBA contributes to the development of biosensors and biomaterials by facilitating the immobilization of biomolecules onto surfaces. For example, enzymes or antibodies can be immobilized on sensor chips using SBA, enabling the creation of biosensors for specific biomolecule detection. Similarly, SBA can be used to attach bioactive molecules to biomaterials, potentially enhancing their biocompatibility and functionality in applications like tissue engineering and implant design.
2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid is a compound characterized by its unique pyrrolidine structure, which includes a dioxopyrrolidine moiety. Its molecular formula is , and it has a molecular weight of approximately 227.25 g/mol. The compound features a butanoic acid side chain, which contributes to its biological activity and potential applications in medicinal chemistry. The structure can be represented by the following canonical SMILES notation: CC(C(=O)O)N1C(=O)CCC1=O.
- Esterification: Reaction with alcohols can yield esters, especially in the presence of acid catalysts.
- Amidation: The carboxylic acid can react with amines to form amides.
- Reduction: The carbonyl groups in the dioxopyrrolidine can be reduced to hydroxyl groups using reducing agents such as lithium aluminum hydride.
- Cyclization: Under specific conditions, the compound can participate in cyclization reactions to form more complex structures.
Research indicates that 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid exhibits significant biological activity, particularly in anticonvulsant properties. A study synthesized a library of derivatives based on this compound, demonstrating its potential as a new class of hybrid anticonvulsant agents. These derivatives showed effectiveness in various seizure models, indicating that modifications to the base structure can enhance pharmacological activity .
The synthesis of 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid typically involves several steps:
- Formation of Dioxopyrrolidine: Starting materials are reacted under controlled conditions to form the dioxopyrrolidine core.
- Coupling Reaction: The dioxopyrrolidine is then coupled with butanoic acid derivatives using coupling agents like N,N'-dicyclohexylcarbodiimide (DCC) or N,N-carbonyldiimidazole (CDI).
- Purification: The final product is purified through recrystallization or chromatography to obtain high purity suitable for biological testing.
Industrial methods may employ continuous flow systems for scalability and efficiency while ensuring quality control measures are in place .
The primary applications of 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid lie in medicinal chemistry and drug development:
- Anticonvulsant Drugs: As part of hybrid compounds, it shows promise in treating epilepsy and other seizure disorders.
- Pharmaceutical Research: Its unique structure makes it a candidate for further modifications to enhance therapeutic effects or reduce side effects.
Interaction studies have focused on the compound's ability to bind to various biological targets, particularly in the central nervous system. Preliminary studies suggest that derivatives of 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid interact favorably with neurotransmitter systems involved in seizure propagation, potentially offering new avenues for therapeutic intervention .
Several compounds share structural similarities with 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid. Here are some notable examples:
| Compound Name | Structural Features | Unique Aspects |
|---|---|---|
| 2,5-Dioxopyrrolidin-1-yl 3-methylbutanoate | Similar dioxopyrrolidine core | Methyl substitution alters pharmacokinetics |
| N-Succinimidyl 3-(pyridin-2-yldisulfanyl)propionate | Contains a succinimide ring | Used in bioconjugation applications |
| 2-(3-methyl-2,5-dioxopyrrolidin-1-yl)propanamide | Methyl group on pyrrolidine | Enhanced biological activity as anticonvulsants |
Uniqueness: The unique aspect of 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid lies in its specific combination of structural features that provide optimal stability and reactivity for pharmaceutical applications. Its bifunctional nature allows for versatile modifications that can lead to improved therapeutic profiles compared to other similar compounds .
Carbodiimide reagents, particularly 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide (EDC), are widely employed to activate the carboxylic acid group of 2-(2,5-dioxopyrrolidin-1-yl)butanoic acid for subsequent amide bond formation. The reaction proceeds via the formation of an O-acylisourea intermediate, which reacts with primary amines to yield stable conjugates. Notably, the inclusion of NHS enhances the stability of the activated intermediate, enabling efficient coupling under physiological conditions.
A key advantage of this approach lies in the dual reactivity of the molecule: the NHS ester can act as a leaving group during carbodiimide-mediated activation, while the butanoic acid backbone provides flexibility for spacer arm design. Experimental data from analogous systems demonstrate that optimizing the molar ratio of EDC to NHS significantly improves coupling efficiency. For instance, a 2:1 molar ratio of EDC:NHS in 0.1 M MES buffer (pH 4.5) achieves >90% conversion to the active ester within 30 minutes at 25°C.
| Parameter | Optimal Value | Effect on Yield |
|---|---|---|
| EDC:NHS Ratio | 2:1 | Maximizes intermediate stability |
| pH | 4.5–6.0 | Minimizes hydrolysis |
| Reaction Time | 30–60 minutes | Balances activation and side reactions |
| Solvent | Anhydrous DMF | Enhances carbodiimide solubility |
The choice of solvent profoundly impacts reaction kinetics. Aprotic polar solvents like dimethylformamide (DMF) stabilize the O-acylisourea intermediate, whereas aqueous systems require precise pH control to prevent premature hydrolysis. Recent studies using 2-(2,5-dioxopyrrolidin-1-yl)butanoic acid derivatives in peptide synthesis demonstrate that introducing electron-withdrawing substituents on the pyrrolidinedione ring increases electrophilicity, enabling coupling reactions with sterically hindered amines.
Solid-Phase Synthesis Approaches for Hybrid Analogues
Solid-phase synthesis techniques have been adapted to create hybrid analogues of 2-(2,5-dioxopyrrolidin-1-yl)butanoic acid, particularly for applications in targeted drug delivery and biomaterial functionalization. The NHS ester moiety serves as a handle for immobilizing the compound onto amine-functionalized resins, enabling iterative coupling cycles.
A representative protocol involves:
- Resin Activation: Aminomethyl polystyrene resin is treated with EDC and NHS in dichloromethane to generate reactive sites.
- Acid Coupling: 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid (0.2 M in DMF) is flowed through the resin bed at 4°C for 12 hours.
- Capping: Unreacted amines are blocked with acetic anhydride to prevent undesired side reactions.
This methodology enables the synthesis of dendrimeric structures with precise control over branching density. For example, coupling the acid to tris(2-aminoethyl)amine cores yields tetravalent conjugates with enhanced binding avidity in protein-ligand systems. The solid-phase approach also facilitates the incorporation of fluorophores or affinity tags via orthogonal protection strategies, as demonstrated in the synthesis of multimodal imaging probes.
Optimization of Leaving Group Stability in Aprotic Solvents
The stability of the NHS leaving group in 2-(2,5-dioxopyrrolidin-1-yl)butanoic acid derivatives governs their utility in multistep syntheses. Kinetic studies in anhydrous DMF reveal that the half-life of the NHS ester at 25°C exceeds 72 hours, compared to <2 hours in aqueous buffers at pH 7.4. This stability enables purification and storage of activated intermediates for subsequent reactions.
Three critical factors influence leaving group stability:
- Solvent Dielectric Constant: Lower dielectric media (ε = 36.7 for DMF) reduce water ingress and hydrolysis rates.
- Temperature Control: Storage at -20°C decreases degradation by 85% over 30 days compared to room temperature.
- Additive Effects: Inclusion of molecular sieves (4Å) absorbs residual moisture, extending functional group integrity.
Recent advances employ computational modeling to predict hydrolysis rates based on solvent accessible surface area (SASA) of the NHS moiety. Molecular dynamics simulations correlate increased SASA (>110 Ų) with faster degradation, guiding the design of sterically shielded derivatives. These insights have been applied to develop photoactivatable variants where the NHS ester remains inert until UV irradiation cleaves a protecting group, enabling spatiotemporal control over conjugation events.
The succinimide ester group in 2-(2,5-dioxopyrrolidin-1-yl)butanoic acid undergoes nucleophilic acyl substitution primarily with amine-containing biomolecules, forming stable amide bonds. This reaction is pH-dependent, as the deprotonation state of the amine nucleophile dictates its reactivity. At physiological pH (7.0–8.5), primary amines (e.g., lysine side chains in proteins) exist in a partially deprotonated state, enabling nucleophilic attack on the carbonyl carbon of the succinimide ester [7] [8].
The mechanism proceeds through a tetrahedral intermediate, where the amine attacks the electrophilic carbonyl carbon, leading to the expulsion of the succinimide leaving group. Studies using infrared spectroscopy (IR) and X-ray photoelectron spectroscopy (XPS) have confirmed the formation of amide bonds during this process [4] [5]. For example, in borate buffer (pH 8.5), the reaction between succinimide esters and ethylamine exhibits a pseudo first-order rate constant ($$k_a'$$) of $$1.2 \times 10^{-3} \, \text{s}^{-1}$$, highlighting the efficiency of this pathway under alkaline conditions [5].
The steric and electronic properties of the succinimide ring further influence reactivity. Molecular docking studies demonstrate that substituents on the pyrrolidine ring modulate the electrophilicity of the carbonyl group, with electron-withdrawing groups enhancing reactivity [1]. For instance, the introduction of a benzyl substituent in derivatives like (R)-AS-1 increases the electrophilicity of the ester, accelerating amide bond formation [1].
Solvent Effects on Anhydride Intermediate Formation
Solvent polarity and proticity significantly impact the stability of intermediates in succinimide ester reactions. In polar aprotic solvents like dimethyl sulfoxide (DMSO), the formation of anhydride intermediates is favored due to reduced solvation of the electrophilic carbonyl group [7] [2]. Density functional theory (DFT) calculations reveal that in DMSO, the activation energy barrier for anhydride formation decreases by 15–20% compared to aqueous environments [2].
Conversely, protic solvents such as water promote hydrolysis via stabilization of the transition state through hydrogen bonding. For example, in aqueous borate buffer (pH 8.5), the hydrolysis rate constant ($$k_h'$$) of succinimide esters is $$3.5 \times 10^{-3} \, \text{s}^{-1}$$, nearly threefold higher than the aminolysis rate [5]. This disparity arises from the rapid nucleophilic attack of hydroxide ions on the ester carbonyl, a process accelerated by the high dielectric constant of water [4].
Table 1: Solvent Effects on Reaction Pathways
| Solvent | Dielectric Constant | Dominant Pathway | Rate Constant ($$s^{-1}$$) |
|---|---|---|---|
| DMSO | 47.2 | Anhydride formation | $$2.8 \times 10^{-3}$$ [2] |
| Water | 80.1 | Hydrolysis | $$3.5 \times 10^{-3}$$ [5] |
| Ethanol | 24.3 | Mixed | $$1.1 \times 10^{-3}$$ [2] |
Hydration effects further modulate reactivity. Three-dimensional reference interaction site model (3D-RISM) simulations show that water molecules stabilize bent conformations of intermediates, reducing the energy required for hydrolysis [2]. In contrast, nonpolar solvents stabilize linear intermediates, favoring aminolysis [2].
Comparative Kinetics of Hydrolysis vs. Amine Coupling
The competition between hydrolysis and amine coupling is a critical determinant of bioconjugation efficiency. Kinetic studies using IR spectroscopy demonstrate that hydrolysis follows a pseudo first-order rate law ($$k_h' = 3.5 \times 10^{-3} \, \text{s}^{-1}$$), while aminolysis exhibits substrate-dependent kinetics [5]. At low amine concentrations (e.g., <100 mM), hydrolysis dominates, with less than 20% of esters participating in amide bond formation [4].
Table 2: Rate Constants for Hydrolysis and Aminolysis
| Condition | $$k_h' \, (\text{s}^{-1})$$ | $$k_a' \, (\text{s}^{-1})$$ |
|---|---|---|
| Borate buffer (pH 8.5) | $$3.5 \times 10^{-3}$$ [5] | $$1.2 \times 10^{-3}$$ [5] |
| 20% Dioxane | $$8.6 \times 10^{-2}$$ [5] | $$5.7 \times 10^{-2}$$ [5] |
The pH dependence of these reactions is pronounced. At pH 7.4, the aminolysis rate increases by 40% compared to pH 6.0, whereas hydrolysis remains relatively constant [7]. This is attributed to the deprotonation of amine groups, which enhances their nucleophilicity. For example, the p$$K_a$$ of lysine ε-amino groups is ~10.5, meaning that at physiological pH, a small fraction exists in the reactive deprotonated state [5].
Molecular dynamics simulations further reveal that steric hindrance in crowded environments (e.g., protein surfaces) reduces aminolysis efficiency. In such cases, hydrolysis accounts for over 70% of ester consumption [4]. To mitigate this, recent strategies employ high local concentrations of amines or organic cosolvents to shift the equilibrium toward amide bond formation [7] [8].
Density Functional Theory Analysis of Carbonyl Attack Geometries
The computational analysis of carbonyl attack geometries in 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid requires sophisticated density functional theory methods to accurately describe the transition state structures and energetics [1] [2]. The approach of nucleophiles to the carbonyl carbon follows the well-established Bürgi-Dunitz trajectory, which defines the optimal angle of nucleophilic attack at approximately 107 degrees [3] [4] [5]. This geometric constraint emerges from the overlap between the lowest unoccupied molecular orbital of the carbonyl function and the highest occupied molecular orbital of the nucleophile [6].
Modern density functional theory calculations employ various exchange-correlation functionals and basis sets to optimize transition state geometries with high accuracy [7] [8]. The PBE-D3 functional combined with 6-31G(d) basis sets provides reliable transition state optimizations, while single-point energy calculations using PBE-D3/6-311+G(d,p) deliver enhanced accuracy for energetic predictions [9]. These computational protocols have been validated against high-level coupled cluster methods, particularly DLPNO-CCSD(T), which serves as the benchmark for barrier height calculations [8].
Table 1: Computational Methods for Carbonyl Activation Studies
| Method | Application | Accuracy | Computational Cost |
|---|---|---|---|
| PBE-D3/6-31G(d) | Transition state optimization | Moderate | Medium |
| PBE-D3/6-311+G(d,p) | Single-point energy calculations | High | High |
| B3LYP/SV(P) | General DFT calculations | Good | Medium |
| BP/SV(P) | RI method optimization | Good | Low |
| DLPNO-CCSD(T) | High-accuracy benchmark | Very High | Very High |
| GFN1-xTB | Semiempirical calculations | Fast screening | Very Low |
The geometrical analysis of transition states reveals that nucleophilic attack on the carbonyl carbon of 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid follows predictable patterns based on orbital interactions [10]. The carbonyl group exhibits sp2 hybridization with three sigma bonds and one pi bond, where the pi-star orbital serves as the electron acceptor during nucleophilic approach [11]. The angle of attack deviates from the perpendicular approach due to electrostatic repulsion between the nucleophile and the oxygen lone pairs, resulting in the characteristic 107-degree Bürgi-Dunitz angle [5] [6].
Table 2: Bürgi-Dunitz Angle Computational Results
| System | Angle (degrees) | Method | Reference |
|---|---|---|---|
| General Carbonyl | 107 | SCF-LCAO-MO | Historical |
| CN⁻ + (CH₃)₂C=O | 107 | 2D Energy Decomposition | Recent 2D Analysis |
| Gas Phase Calculation | 105 | DFT Gas Phase | Static Optimization |
| Implicit Solvent | 105 | SMD Solvation | Continuum Model |
| Crystallographic | 107 | X-ray Analysis | Experimental |
The computational analysis demonstrates that solvent effects significantly influence transition state geometries, with implicit solvation models showing compressed attack angles compared to gas-phase calculations [9]. The SMD continuum solvation model reveals that hydrogen bonding interactions with solvent molecules can stabilize certain transition state conformations while destabilizing others [9]. These findings indicate that accurate modeling of 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid reactivity requires explicit consideration of environmental effects [2] [12].
Charge Distribution Mapping in N-Hydroxysuccinimide Ester Complexes
The charge distribution analysis in N-hydroxysuccinimide ester complexes provides crucial insights into the electronic structure and reactivity patterns of 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid derivatives [13] [14]. Electrostatic potential mapping serves as a fundamental tool for visualizing charge distributions across molecular surfaces, enabling the identification of electron-rich and electron-deficient regions that govern chemical reactivity [13] [15].
The molecular electrostatic potential calculation involves determining the electrostatic potential energy at specified distances from atomic nuclei, creating three-dimensional representations of charge distributions [13] [15]. These calculations reveal that the carbonyl carbon in N-hydroxysuccinimide esters exhibits significant positive electrostatic potential, making it highly susceptible to nucleophilic attack [16] [17]. The color-coded representation typically employs red coloring for electron-rich regions with negative electrostatic potential and blue coloring for electron-deficient areas with positive potential [14] [15].
Table 3: Charge Distribution Analysis Methods
| Method | Application | Advantages | Limitations |
|---|---|---|---|
| Electrostatic Potential Mapping | Visual charge distribution | Intuitive visualization | Qualitative |
| Natural Bond Orbital (NBO) | Electron delocalization | Physical insight | Computationally intensive |
| CM5 Atomic Charges | Machine learning models | ML compatibility | Basis set dependent |
| Mulliken Charges | Simple charge analysis | Fast calculation | Poor transferability |
| CHELPG Charges | Electrostatic fitting | Accurate ESP reproduction | Grid dependent |
Natural bond orbital analysis provides quantitative measures of electron delocalization and charge transfer within N-hydroxysuccinimide ester complexes [18]. The NBO method reveals the stabilization energies corresponding to interactions between different molecular orbitals, offering insights into hydrogen bonding strength and hyperconjugative effects [18]. These calculations demonstrate that the succinimide ring system exhibits significant electron delocalization, which influences the reactivity of the adjacent carbonyl group [19].
The charge analysis of 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid reveals that the nitrogen atom in the succinimide ring carries a partial positive charge due to the electron-withdrawing nature of the two adjacent carbonyl groups [19]. This electronic configuration enhances the electrophilicity of the ester carbonyl carbon, making it more reactive toward nucleophilic species [16] [17]. The electrochemical studies of related succinimide derivatives confirm these computational predictions, showing that electron transfer processes occur preferentially at specific carbon positions [19].
Spin density calculations provide additional information about radical intermediates formed during electrochemical oxidation of succinimide compounds [19]. These studies reveal that radical formation occurs primarily at carbon atoms adjacent to the nitrogen, with significant delocalization over neighboring aromatic rings when present [19]. The computational analysis indicates that the stability of these radical intermediates depends on the extent of electron delocalization and the presence of electron-donating or electron-withdrawing substituents [19].
Predictive Models for Regioselectivity in Polyfunctional Systems
The development of predictive models for regioselectivity in polyfunctional systems containing 2-(2,5-Dioxopyrrolidin-1-yl)butanoic acid derivatives represents a significant advancement in computational chemistry [20] [21] [22]. Machine learning approaches combined with quantum mechanical descriptors have emerged as powerful tools for predicting reaction outcomes with high accuracy and minimal computational cost [22] [23].
The RegioML model, developed for predicting regioselectivity in electrophilic aromatic substitution reactions, achieves 93% accuracy using CM5 atomic charges computed with semiempirical tight binding methods [20] [24]. This approach demonstrates that relatively simple atomic charge descriptors can capture the essential electronic features governing regioselectivity when combined with appropriate machine learning algorithms [20]. The light gradient boosting machine algorithm proves particularly effective for this application, handling large datasets with over 100,000 reaction centers [20] [24].
Table 4: Regioselectivity Prediction Model Performance
| Model Type | Accuracy (%) | Precision (%) | Dataset Size | Reaction Type |
|---|---|---|---|---|
| RegioML | 93.0 | 88.0 | 21,201 reactions | Electrophilic aromatic |
| WLN Graph-based | 93.0 | 85.0 | Large dataset | Various |
| Physics-based RegioSQM20 | 75.0 | 75.0 | Synthetic data | General |
| Fusion GNN + QM | 96.3 | 94.7 | Pfizer internal | SNAr reactions |
| Machine Learning + DFT | 89.7 | 89.7 | 5,000 reactions | Substitution reactions |
Advanced fusion models that combine graph neural networks with quantum mechanical calculations achieve even higher accuracy rates, with some systems reporting 96.3% accuracy for nucleophilic aromatic substitution reactions [21]. These hybrid approaches leverage the pattern recognition capabilities of machine learning while incorporating the physical insights provided by quantum mechanical descriptors [21] [22]. The integration of on-the-fly quantum mechanical calculations enables the models to adapt to new chemical spaces without extensive retraining [22].
Target-specific dataset design strategies have proven effective for improving regioselectivity predictions on complex substrates [23] [25]. The development of acquisition functions that selectively choose the most informative training examples reduces the dataset size requirements by more than 50% while maintaining prediction accuracy [23] [26]. These active learning approaches are particularly valuable for late-stage functionalization reactions where experimental data may be limited [26] [25].
The computational workflow for regioselectivity prediction typically involves hierarchical quantum mechanical calculations, starting with fast semiempirical methods for initial screening followed by higher-level density functional theory calculations for refined predictions [27]. This multi-level approach balances computational efficiency with accuracy, enabling the rapid evaluation of multiple reaction sites in complex polyfunctional molecules [27]. The integration of directing group effects and catalyst considerations further enhances the predictive capability of these models [12] [27].