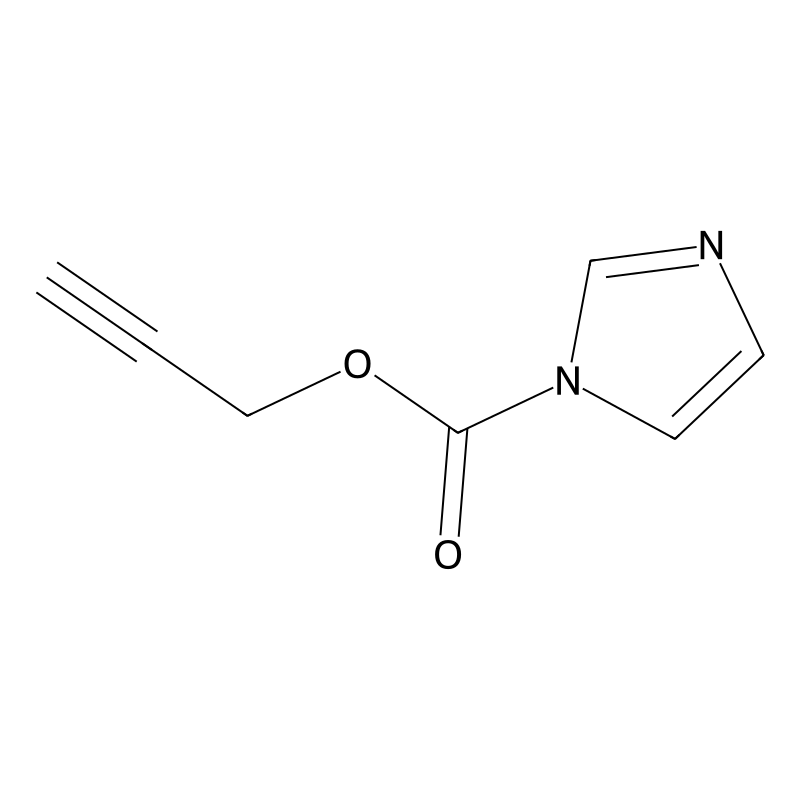
Prop-2-yn-1-yl 1H-imidazole-1-carboxylate

Prop-2-yn-1-yl 1H-imidazole-1-carboxylate (CAS 83395-38-4), commonly known as a Heller-Sarpong reagent, is a stable, crystalline activated carbamate utilized primarily for the chemoselective propargylation of carboxylic acids and the N-acylation of heterocycles. Functioning as an efficient propargyloxycarbonyl (Poc) transfer agent, it enables the installation of terminal alkyne handles essential for downstream Cu(I)-catalyzed Azide-Alkyne Cycloaddition (CuAAC) click chemistry. Its robust shelf-stability and crystalline nature make it a practical procurement alternative for scalable pharmaceutical synthesis and bioconjugation workflows, providing a mild, high-yielding substitute to highly toxic or explosive alkylating agents[1].

Substituting Prop-2-yn-1-yl 1H-imidazole-1-carboxylate with conventional propargylating agents such as propargyl bromide, propargyl chloroformate, or propargyl alcohol/carbodiimide systems introduces severe process and safety liabilities. Propargyl bromide is highly toxic, poses explosive hazards, and exhibits poor chemoselectivity in the presence of competing nucleophiles. Propargyl chloroformate is notoriously corrosive, highly moisture-sensitive, and prone to rapid degradation during storage, leading to inconsistent batch-to-batch reproducibility. Furthermore, standard carbodiimide-mediated esterification with propargyl alcohol often results in the racemization of epimerizable stereocenters and generates stoichiometric urea byproducts that complicate downstream purification. The Heller-Sarpong reagent bypasses these failure modes by providing a shelf-stable, chemoselective pathway that operates under mild conditions, ensuring high-fidelity esterification without the handling risks or purification bottlenecks of generic alternatives [1].

Propargyl Esterification Efficiency

In the synthesis of propargyl esters, Prop-2-yn-1-yl 1H-imidazole-1-carboxylate demonstrates strong quantitative efficiency under mild conditions. When reacted with 4-bromophenylacetic acid, the reagent delivered the corresponding propargyl ester in an 87% isolated yield. This performance highlights its utility as a direct replacement for hazardous propargyl bromide or moisture-sensitive chloroformates, providing a clean, high-yielding route to alkyne-functionalized building blocks[1].

Enables procurement teams to source a safer, high-yielding reagent for click-chemistry precursor synthesis, eliminating the regulatory and safety overhead of explosive propargyl halides.

Substrate Scope and Byproduct Removal

The Heller-Sarpong reagent facilitates the conversion of a wide variety of aliphatic and aromatic carboxylic acids into their corresponding propargyl esters with isolated yields consistently ranging from 70% to 93%. Unlike traditional carbodiimide (e.g., DCC or EDC) coupling methods that generate stubborn stoichiometric urea byproducts, this imidazole carbamate pathway produces only imidazole and carbon dioxide as byproducts, which are easily removed via simple aqueous workup [1].

Streamlines downstream purification processes in B2B manufacturing by eliminating difficult-to-remove urea byproducts, reducing solvent waste and labor costs.

Selective N-Acylation of Heterocycles

Beyond esterification, carbonylazole reagents like Prop-2-yn-1-yl 1H-imidazole-1-carboxylate enable the highly chemoselective N-acylation of indoles and oxazolidinones. Utilizing catalytic amounts of DBU (50 mol%), these reagents selectively acylate non-nucleophilic nitrogen atoms even in the presence of more reactive competing nucleophiles such as anilines or phenols. This orthogonal reactivity cannot be achieved with standard propargyl chloroformate, which indiscriminately attacks the most nucleophilic sites [1].

Allows synthetic chemists to perform complex late-stage functionalization and orthogonal protecting group strategies, significantly shortening synthetic routes.

Click-Chemistry Precursor Synthesis

Due to its ability to deliver propargyl esters in high yields (70-93%) without the use of toxic propargyl halides, this compound serves as an efficient reagent for installing terminal alkyne handles on carboxylic acid-containing pharmaceuticals or biomolecules. This enables seamless downstream integration into Cu(I)-catalyzed Azide-Alkyne Cycloaddition (CuAAC) workflows for bioconjugation and materials science[1].

Late-Stage API Functionalization

The reagent's specific chemoselectivity, particularly its ability to N-acylate indoles and oxazolidinones in the presence of more reactive amines or phenols under DBU catalysis, makes it highly valuable for the late-stage functionalization of complex Active Pharmaceutical Ingredients (APIs). It allows chemists to bypass multi-step protection/deprotection sequences [2].

Scalable Pharmaceutical Manufacturing

For industrial scale-up, the stability of Prop-2-yn-1-yl 1H-imidazole-1-carboxylate offers a significant procurement advantage over moisture-sensitive propargyl chloroformate. Furthermore, the elimination of stoichiometric urea byproducts (common with DCC/EDC couplings) drastically simplifies aqueous workups, reducing solvent consumption and labor costs during bulk manufacturing [1].