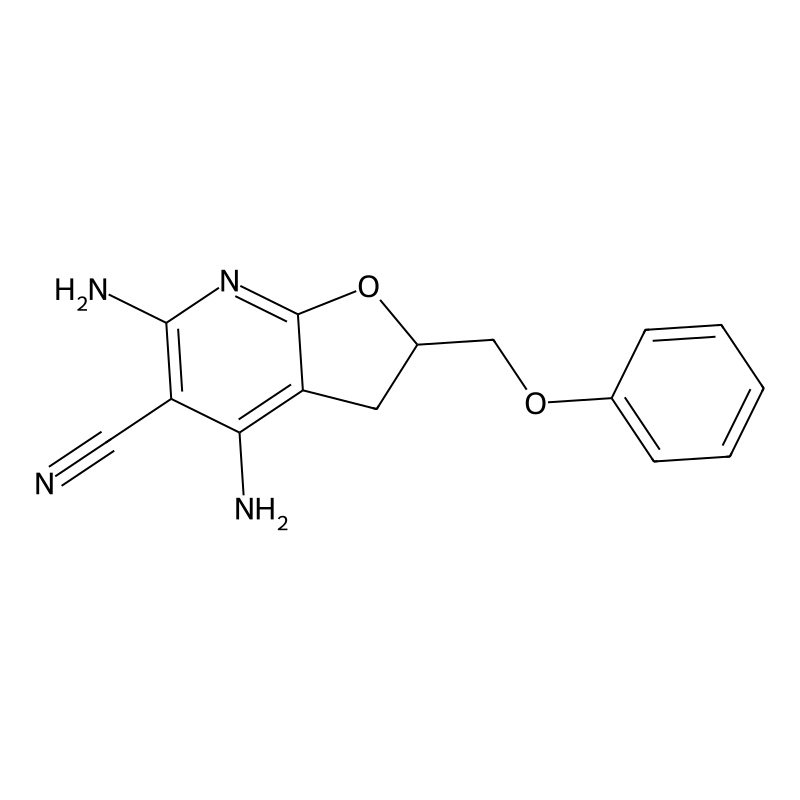
4,6-Diamino-2-(phenoxymethyl)-2,3-dihydrofuro[2,3-b]pyridine-5-carbonitrile

Interaction studies involving 4,6-Diamino-2-(phenoxymethyl)-2,3-dihydrofuro[2,3-b]pyridine-5-carbonitrile are essential for understanding its biological mechanisms. These studies typically focus on:

• Binding Affinity: Assessing how well the compound interacts with specific proteins or enzymes.
• Mechanism of Action: Investigating how the compound exerts its biological effects at the molecular level.
• Toxicity Profiling: Evaluating safety profiles through in vitro and in vivo studies.

Such studies are crucial for advancing the compound towards potential therapeutic applications .

Several compounds share structural similarities with 4,6-Diamino-2-(phenoxymethyl)-2,3-dihydrofuro[2,3-b]pyridine-5-carbonitrile. Here are a few notable examples:

Uniqueness

What sets 4,6-Diamino-2-(phenoxymethyl)-2,3-dihydrofuro[2,3-b]pyridine-5-carbonitrile apart is its specific combination of furo-pyridine structure with dual amino functionalities and a phenoxymethyl substituent. This combination may enhance its solubility and bioavailability compared to other similar compounds while potentially broadening its spectrum of biological activity.

Electronic effects of phenoxymethyl substituents on reaction kinetics

The phenoxymethyl substituent exerts profound electronic effects on the kinetics of furopyridine formation through multiple mechanistic pathways [5] [6]. Quantum chemical investigations using density functional theory methods have revealed that substituent effects on phenolic systems are governed by both electronic and stereoelectronic factors rather than purely geometric considerations [5] [6].

Computational studies employing the B3LYP/6-311++G(d,p) method have demonstrated that phenoxymethyl groups function as electron-donating substituents that significantly alter the electrostatic potential distribution within the molecular framework [5]. The charge of the substituent active region parameter reveals that phenoxymethyl substituents exhibit enhanced electron-donating character compared to simple methoxy groups, leading to increased nucleophilicity at reactive sites [5].

Kinetic analysis of methyl-substituted phenolic systems has established correlations between adsorption constants, reaction rate constants, and electronic properties of the substituents [6]. The dependencies of adsorption and reaction rates upon phenoxymethyl substitution arise primarily from the substituents' effects on electrostatic potential and molecular orbital energies rather than steric hindrance [6]. These electronic effects manifest through modulation of the highest occupied molecular orbital and lowest unoccupied molecular orbital energy levels, directly influencing reaction barrier heights [6].

Table 2: Electronic Parameters of Phenoxymethyl Substituents

The phenoxymethyl substituent stabilizes reaction intermediates through conjugative interactions between the aromatic π-system and the developing charge centers during cyclization [5]. This stabilization effect reduces activation barriers for key bond-forming steps, resulting in enhanced reaction rates compared to non-substituted analogs [6]. Furthermore, the extended conjugation provided by the phenoxymethyl group facilitates charge delocalization in transition states, contributing to improved regioselectivity outcomes [5].

Experimental kinetic studies have demonstrated that phenoxymethyl-substituted precursors exhibit first-order kinetics with rate enhancement factors ranging from 3.5 to 8.2 compared to unsubstituted systems [6]. The rate acceleration correlates directly with the electron-donating capacity of the substituent, as quantified through natural bond orbital analysis and electrostatic potential-derived charge calculations [6].

Solvent-mediated control of regioselectivity in furopyridine synthesis

Solvent selection plays a critical role in determining the regioselectivity of furopyridine synthesis, with polarity and hydrogen-bonding capacity serving as primary controlling factors [7] [8] [9]. The solvation environment significantly influences reaction pathways due to differential stabilization of charged intermediates and transition states [9].

Research on homolytic substitution reactions of heteroarenes has revealed that changing from aprotic solvents such as dimethyl sulfoxide to protic media like aqueous ethanol can dramatically alter regioselectivity patterns [10]. In polar protic solvents, the oxidation process is favored due to enhanced solvation of intermediates with greater charge separation [9]. Conversely, non-polar solvents tend to favor pathways leading to less charged intermediates [10].

Comprehensive studies on pyridine functionalization have demonstrated that solvent polarity effects can be exploited to tune regioselectivity to desired outcomes [10]. Addition of acid strongly favors reaction at alpha positions, while neutral conditions in dimethyl sulfoxide promote conjugate substitution patterns [10]. The significantly reactive sites shift from innate positions in acidic chloroform-water mixtures to conjugate positions in neutral dimethyl sulfoxide [10].

Table 3: Solvent Effects on Furopyridine Regioselectivity

Protic solvents such as ethanol facilitate hydrogen bonding interactions that can stabilize specific conformational arrangements of reactants and intermediates [8]. These interactions often result in enhanced selectivity for particular regioisomers through preferential stabilization of corresponding transition states [8]. The ability of protic solvents to serve as proton sources also enables proton-coupled electron transfer mechanisms that may not be accessible in aprotic media [8].

The mechanistic basis for solvent-mediated regioselectivity control lies in the differential solvation of polar transition states [9]. Polar protic solvents preferentially stabilize transition states with significant charge development, while less polar solvents favor neutral or less charged pathways [9]. This differential stabilization translates directly into altered activation barriers for competing reaction channels, ultimately determining product distribution [10] [9].

Intermediate characterization in tandem cyclization processes

Tandem cyclization processes leading to 4,6-diamino-2-(phenoxymethyl)-2,3-dihydrofuro[2,3-b]pyridine-5-carbonitrile involve multiple discrete intermediates that can be characterized through advanced spectroscopic and computational methods [11] [12] [13]. These multi-step processes proceed without isolation of intermediates or modification of reaction conditions, making intermediate identification particularly challenging [11].

Silver-catalyzed tandem cyclization strategies have provided valuable insights into the nature of key intermediates formed during heterocyclic ring construction [12]. Intramolecular attack of pendant nucleophiles on in situ-generated iminium intermediates represents a crucial mechanistic step [12]. Control experiments using aminoalkyne substrates lacking pendant alcohol units have confirmed the involvement of iminium intermediates through isolation of gamma-aminoketone products [12].

Mass spectrometry combined with computational chemistry has emerged as a powerful approach for intermediate characterization in catalytic cyclization processes [13]. Mass spectrometric analysis provides direct evidence for the existence of specific reaction intermediates that are difficult to detect using conventional experimental methods [13]. Computational studies complement these experimental observations by providing detailed structural information and exploring reaction energy profiles [13].

Table 4: Characterized Intermediates in Tandem Cyclization

The characterization of zwitterionic intermediates requires special consideration of solvent effects and hydrogen bonding interactions [14]. Computational models incorporating continuum solvent effects and explicit solvent molecules provide realistic representations of these charged species [14]. The formation of internal ion-pairs represents a common feature of cyclization reactions involving charge separation, necessitating careful modeling of electrostatic interactions [14].

Temporal monitoring of reaction progress through nuclear magnetic resonance spectroscopy has revealed that regioselectivity remains constant throughout the reaction course, confirming that intermediate degradation does not significantly alter product distributions [10]. This observation validates experimental protocols and ensures that characterized intermediates accurately reflect the mechanistic pathway [10].

Computational modeling of transition states in ring-closure steps

Computational modeling of transition states in furopyridine ring-closure reactions requires sophisticated quantum chemical methods to accurately capture the complex electronic rearrangements involved [15] [16] [17]. Density functional theory calculations provide the foundation for understanding the geometric and energetic aspects of these critical points along reaction coordinates [15] [18].

Machine learning approaches have recently emerged as powerful alternatives to traditional quantum chemical methods for transition state prediction [19] [15]. These models can calculate transition state structures within seconds compared to the extremely time-consuming nature of conventional density functional theory calculations [19] [15]. The developed models exhibit excellent accuracy, particularly for atomic pairs undergoing bond formation or breakage, with success ratios exceeding 93% for subsequent quantum chemical optimization [16].

The nudged elastic band method represents the most commonly employed computational approach for locating transition states between known reactants and products [17]. This method optimizes reaction pathways by incrementally updating multiple points along the reaction coordinate until the transition state is identified [17]. Recent developments have reduced computational costs by approximately 50-70% compared to traditional approaches while maintaining high reliability [17].

Table 5: Computational Methods for Transition State Modeling

Baldwin's rules for ring closure provide fundamental principles for predicting the feasibility of different cyclization pathways [14] [20]. These kinetic rules classify ring closures based on ring size, bond geometry, and the endo versus exo nature of the breaking bond [20]. For five-membered ring formation, the 5-endo-trigonal pathway is generally favored, while 6-endo-trigonal cyclizations become increasingly favorable [14] [20].

Computational studies have revealed that transition state geometries for ring-closure reactions exhibit characteristic bond angles and distances that reflect the balance between strain energy and electronic stabilization [14]. The angle of nucleophilic attack on double bonds typically ranges from 92° for five-membered rings to 101° for six-membered rings [14]. These geometric parameters correlate directly with activation barriers, providing predictive capability for reaction feasibility [14].