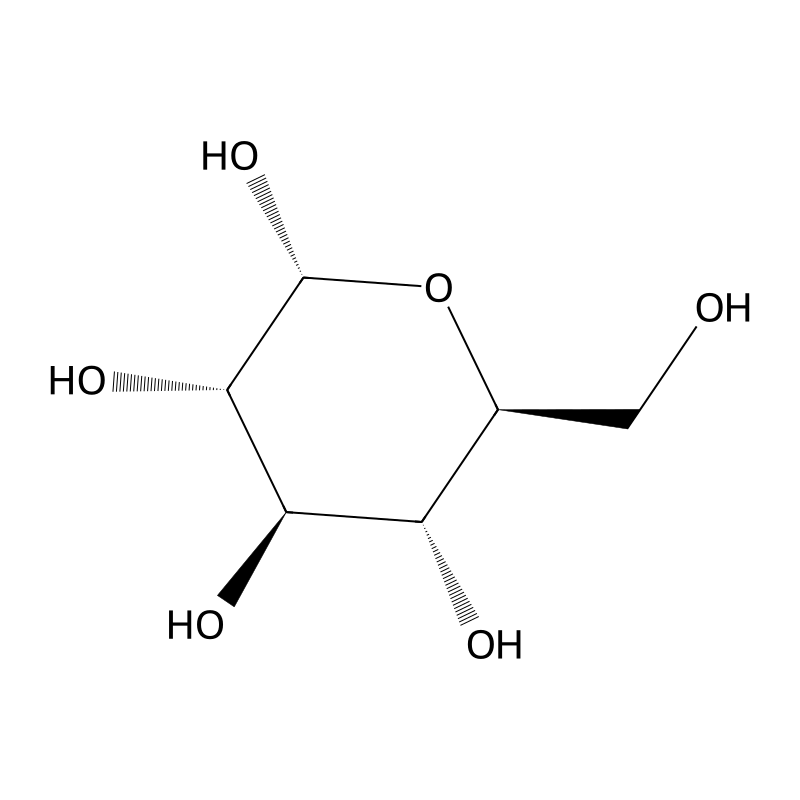
alpha-L-glucopyranose

alpha-L-Glucopyranose (CAS 492-66-0) is the pure alpha-anomer of the non-naturally occurring L-enantiomer of glucose. In commercial and research procurement, it serves two primary functions: as an absolute stereochemical negative control in metabolic and transport assays, and as a highly defined chiral building block for the synthesis of L-nucleosides and L-glycoconjugates. Unlike naturally abundant D-glucose, alpha-L-glucopyranose is completely resistant to phosphorylation by hexokinase and evades standard glycolytic pathways [1]. Furthermore, its defined anomeric stereochemistry makes it a more efficient precursor than mixed-anomer L-glucose for complex synthetic applications, where predictable stereocontrol during glycosylation is critical for yield and purity [2].

Substituting alpha-L-glucopyranose with generic L-glucose (a fluctuating mixture of alpha and beta anomers) severely compromises synthetic workflows. In the synthesis of antiviral L-nucleosides, anomeric mixtures lead to poor diastereoselectivity during the critical glycosylation step, requiring expensive and low-yield chromatographic separations of the resulting nucleoside epimers [1]. Conversely, substituting with D-glucose or 2-deoxy-D-glucose in metabolic assays fails because D-glucose is rapidly metabolized, and 2-deoxy-D-glucose is actively phosphorylated by hexokinase, confounding transport data with intracellular trapping [2]. Only the pure alpha-L-anomer provides both the metabolic inertness required for baseline transport studies and the stereochemical purity necessary for high-yield downstream synthesis.

Absolute Resistance to Hexokinase Phosphorylation

In comparative metabolic assays, alpha-L-glucopyranose demonstrates complete resistance to phosphorylation by hexokinase, serving as a strict zero-background control. While D-glucose exhibits a high maximal phosphorylation rate (e.g., Vmax ~55 nmol/min/mg protein in specific cell models) and 2-deoxy-D-glucose is also readily phosphorylated and trapped intracellularly, L-glucose remains entirely unphosphorylated. This absolute enzymatic stereospecificity ensures that any intracellular accumulation of L-glucose is strictly a function of transport dynamics, not metabolic trapping[1].

Procurement of this exact enantiomer is mandatory for assays requiring a metabolically inert glucose analog to isolate membrane transport kinetics from intracellular glycolysis.

Anomeric Purity for Stereoselective L-Nucleoside Synthesis

The synthesis of therapeutically relevant L-nucleosides requires strict stereocontrol to ensure the correct beta-L configuration of the final drug substance. Utilizing pure alpha-L-glucopyranose as the starting material allows for highly diastereoselective glycosylation via neighboring group participation or direct SN2-like inversion at the anomeric center. In contrast, utilizing generic mixed-anomer L-glucose (CAS 921-60-8) results in a mixture of alpha and beta nucleosides, significantly reducing the yield of the target epimer and necessitating costly downstream purification[1].

For industrial scale-up of L-nucleoside antivirals, starting with the pure alpha-anomer drastically reduces purification costs and improves target yield.

Selective SGLT1 Transport vs. GLUT Exclusion

alpha-L-glucopyranose is specifically utilized to differentiate between active sodium-dependent glucose transport and passive or GLUT-mediated transport. Pharmacokinetic studies demonstrate that L-glucose is transported across the intestinal epithelium primarily via SGLT1, but it is virtually excluded by most facilitative GLUT transporters (unlike D-glucose, which is rapidly transported by both). When SGLT1-specific inhibitors (e.g., KGA-2727) are applied, the absorption of L-glucose is significantly blocked, confirming its utility as a specific probe for SGLT1 activity and paracellular permeability without the confounding effects of GLUT-mediated cellular uptake [1].

Researchers must procure L-glucose to accurately calibrate SGLT1-specific transport models and measure paracellular leakage without GLUT interference.

Negative Control in Cellular Glucose Transport Assays

Because alpha-L-glucopyranose is not phosphorylated by hexokinase, it is the gold standard for measuring baseline, non-metabolized glucose transport across cell membranes. It allows researchers to decouple transporter kinetics from intracellular glycolytic flux, a distinction impossible to make with D-glucose or 2-deoxy-D-glucose [1].

Precursor for Antiviral L-Nucleoside Synthesis

The defined stereochemistry of the alpha-L-anomer makes it a highly reliable starting material for synthesizing L-nucleoside analogs. Its anomeric purity ensures high stereoselectivity during the glycosylation of nucleobases, avoiding the costly purification of epimeric mixtures that occur when using generic L-glucose [2].

Probe for Intestinal Permeability and SGLT1 Function

In pharmacokinetic and gastroenterological research, alpha-L-glucopyranose is administered to evaluate intestinal barrier integrity and SGLT1-specific transport. Its specific exclusion from GLUT transporters makes it a precise marker for paracellular absorption and sodium-dependent active transport [3].