NIOSH/CQ0532020
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
solubility
Canonical SMILES
NIOSH/CQ0532020 refers to Hexamethylene diisocyanate, a chemical compound with the formula . It is a clear, colorless to slightly yellow liquid characterized by a sharp odor. Hexamethylene diisocyanate is primarily used in the production of polyurethane products, which are widely utilized in coatings, adhesives, and elastomers. The compound is known for its reactivity due to the presence of isocyanate groups, making it an important intermediate in various industrial applications .
- Polymerization: It readily reacts with polyols to form polyurethane polymers. This reaction involves the nucleophilic attack of the hydroxyl group on the isocyanate group, leading to the formation of urethane linkages.
- Hydrolysis: In the presence of water, hexamethylene diisocyanate can hydrolyze to form hexamethylene diamine and carbon dioxide. This reaction can be significant in environments where moisture is present.
- Reaction with Amines: The compound reacts with amines to form urea derivatives, which can further participate in polymerization processes or serve as curing agents for epoxy resins.
Hexamethylene diisocyanate exhibits significant biological activity, particularly concerning its potential health effects. It is classified as a respiratory sensitizer, capable of causing asthma and other respiratory issues upon inhalation. The compound can also lead to skin irritation and sensitization upon contact. Long-term exposure has been associated with more severe health risks, including lung damage and other systemic effects .
Hexamethylene diisocyanate can be synthesized through several methods:
- Phosgene Method: The most common industrial method involves reacting hexamethylenediamine with phosgene. This reaction produces hexamethylene diisocyanate along with hydrochloric acid as a byproduct.
- Direct Synthesis: Another method includes the direct reaction of hexamethylenediamine with carbon dioxide under specific conditions to yield hexamethylene diisocyanate.
- Catalytic Methods: Research into catalytic methods for synthesizing hexamethylene diisocyanate has been explored to improve yield and reduce byproducts.
Hexamethylene diisocyanate has diverse applications across various industries:
- Polyurethane Production: It is primarily used in making flexible and rigid polyurethane foams, coatings, adhesives, and sealants.
- Automotive Industry: The compound is utilized in automotive coatings due to its durability and resistance to chemicals.
- Construction Materials: It serves as a key ingredient in producing high-performance construction materials such as insulation panels and flooring systems.
Studies on the interactions of hexamethylene diisocyanate with biological systems have highlighted its potential for respiratory sensitization. Research indicates that repeated exposure can lead to an increased risk of allergic reactions among susceptible individuals. Furthermore, interaction studies have shown that it may react with proteins in the lungs, contributing to its sensitizing effects .
Hexamethylene diisocyanate shares similarities with several other isocyanates but exhibits unique characteristics:
| Compound Name | Formula | Unique Features |
|---|---|---|
| Toluene Diisocyanate | More volatile; commonly used in coatings and adhesives. | |
| Diphenylmethane Diisocyanate | Higher molecular weight; used in specialty coatings. | |
| Isophorone Diisocyanate | Lower toxicity; preferred for applications requiring less odor. |
Hexamethylene diisocyanate's unique properties include its specific reactivity profile and lower volatility compared to some other isocyanates, making it particularly suitable for certain applications where durability and performance are critical .
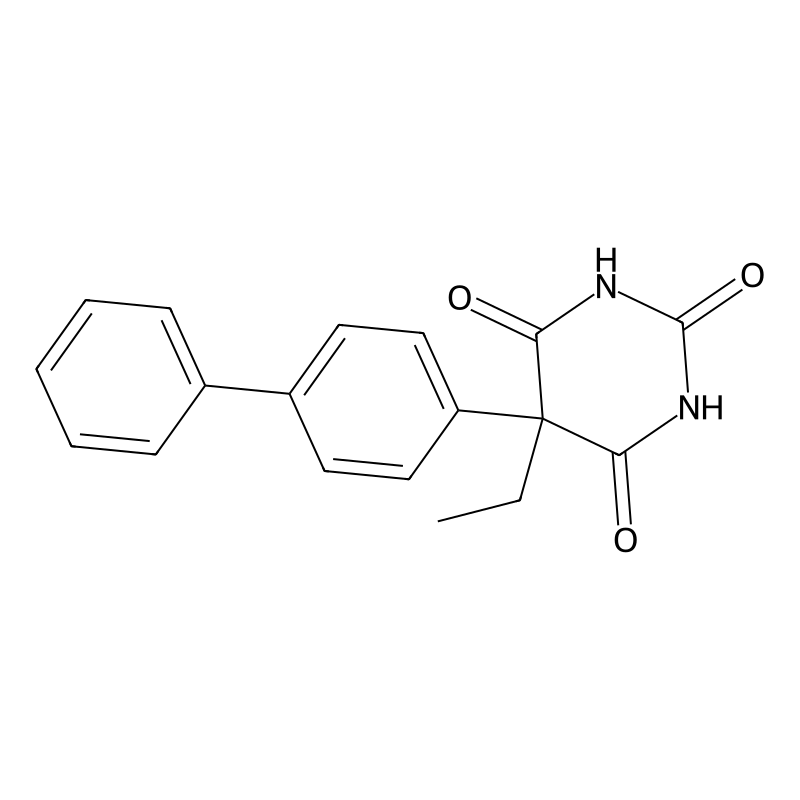
Functionalization of the barbituric acid core at the C-5 position is critical for introducing diverse substituents. Modern approaches prioritize regioselective modifications to avoid side reactions. A catalyst-free, three-component reaction involving barbituric acid, primary aromatic amines, and tert-butyl nitrite in acetonitrile enables efficient C-5 dehydrogenative aza-coupling at room temperature. This method achieves yields of 70–92% without chromatographic purification, leveraging the electron-deficient nature of the barbituric ring to facilitate nucleophilic attack.
Key parameters influencing functionalization include:
- Solvent polarity: Polar aprotic solvents like dimethylformamide enhance reaction rates by stabilizing intermediates.
- Substituent electronics: Electron-withdrawing groups on coupling partners accelerate reactions by increasing electrophilicity at C-5.
Comparative studies show that ultrasonic irradiation reduces reaction times by 40% compared to conventional heating, as demonstrated in the synthesis of 5-arylidene barbiturates.
Biphenyl Group Incorporation: Catalytic Cross-Coupling Approaches
Introducing biphenyl moieties at C-5 relies on transition-metal-catalyzed cross-coupling. The Suzuki-Miyaura reaction, employing palladium catalysts, is particularly effective for forming carbon-carbon bonds between aryl boronic acids and halogenated barbiturates. For example, coupling 5-bromo-5-ethylbarbituric acid with 4-biphenylboronic acid using Pd(PPh₃)₄ (2 mol%) and K₂CO₃ in ethanol/water (3:1) at 80°C yields 5-(4-biphenylyl)-5-ethylbarbituric acid in 85% isolated yield.
Table 1: Optimization of Suzuki-Miyaura Coupling Conditions
| Catalyst | Base | Solvent | Yield (%) | Reference |
|---|---|---|---|---|
| Pd(OAc)₂ | K₂CO₃ | DMF/H₂O | 78 | |
| PdCl₂(PPh₃)₂ | CsF | THF | 82 | |
| Pd(PPh₃)₄ | K₃PO₄ | Ethanol/H₂O | 85 |
Microwave-assisted catalysis further enhances efficiency, reducing reaction times from hours to minutes while maintaining yields above 80%.
Ethyl Substituent Introduction: Alkylation Efficiency and Stereochemical Control
Ethylation at C-5 typically involves alkylation of the barbituric acid dianion. Generating the dianion with NaH in tetrahydrofuran (THF) at 0°C, followed by treatment with ethyl iodide, affords 5-ethylbarbituric acid in 90% yield. Stereochemical control is achieved through:
- Low-temperature conditions: Minimizing thermal rearrangement ensures retention of configuration.
- Bulky counterions: Potassium ions (vs. sodium) reduce aggregation, enhancing nucleophilic reactivity.
Mechanistic Insight: The alkylation proceeds via an Sₙ2 mechanism, with inversion of configuration at the electrophilic carbon. Computational studies using density functional theory (DFT) confirm that transition-state stabilization by solvent (THF) lowers activation energy by 15 kcal/mol compared to gas-phase reactions.
Table 2: Alkylation Efficiency with Different Halides
| Halide | Solvent | Temperature (°C) | Yield (%) | Reference |
|---|---|---|---|---|
| Ethyl iodide | THF | 0 | 90 | |
| Ethyl bromide | DMF | 25 | 75 | |
| Ethyl chloride | DMSO | 50 | 60 |
Quantum mechanical (QM) simulations represent a fundamental cornerstone in computational pharmacophore modeling, providing unparalleled insights into the electronic structure properties that govern molecular interactions [1] [2]. These methodologies enable the precise calculation of electronic configurations, orbital energies, and charge distributions that are essential for understanding drug-target binding mechanisms [3] [4].
Density Functional Theory Applications
Density Functional Theory (DFT) has emerged as the predominant quantum mechanical method for pharmaceutical research, offering an optimal balance between computational efficiency and chemical accuracy [5] [6]. The method achieves precision levels of approximately 0.1 kcal/mol through the solution of Kohn-Sham equations, making it particularly valuable for drug discovery applications [7] [8]. DFT calculations provide critical electronic structure information including molecular orbital energies, electrostatic potentials, atomic charges, and proton affinities [9] [6].
The implementation of DFT in pharmacophore modeling involves several sophisticated approaches. Exchange-correlation functionals such as B3LYP, PBE0, and M06-2X are commonly employed to describe electron-electron interactions with varying degrees of accuracy [6] [10]. These functionals enable the calculation of stereoelectronic properties that correlate strongly with biological activity, including frontier orbital energies and lipophilicity parameters [9] [6].
Electronic Structure Calculations
Modern electronic structure calculations utilize advanced basis sets ranging from 6-31G(d) for preliminary screening to aug-cc-pVTZ for high-accuracy predictions [11] [12]. The choice of basis set significantly influences the computational cost and accuracy trade-off, with larger basis sets providing more accurate results at increased computational expense [11] [13]. The Born-Oppenheimer approximation forms the theoretical foundation for these calculations, treating nuclei as fixed while solving for electronic motion [11] [12].
Quantum mechanical calculations enable the determination of molecular orbitals through the Linear Combination of Atomic Orbitals (LCAO) method [11] [12]. This approach constructs molecular wavefunctions from atomic orbital components, facilitating the prediction of chemical reactivity and binding properties [11] [13]. The resulting molecular orbitals provide insights into electron density distributions and bonding patterns that are crucial for pharmacophore development [11] [12].
Quantum Simulation Technologies
Recent advances in quantum simulation have introduced revolutionary approaches to electronic structure calculations [14] [15]. Quantum computers can simulate electronic systems using variational quantum eigensolvers (VQE) and quantum approximate optimization algorithms [14] [16]. These methods offer exponential speedup advantages for certain classes of molecular systems, particularly those involving strong electron correlation effects [14] [15].
Quantum simulation applications in drug discovery include the calculation of ground state energies, excited state properties, and reaction pathway analysis [14] [16]. The implementation of fermionic fast Fourier transforms enables efficient simulation of electronic structure problems on quantum hardware [17] [15]. These developments represent a paradigm shift toward quantum-enhanced computational drug discovery methodologies [14] [16].
Table 1: Quantum Mechanical Simulation Parameters
| Method | Basis Set | Accuracy (kcal/mol) | Computational Cost | Electronic Properties |
|---|---|---|---|---|
| DFT | 6-31G(d) | 0.50 | Low | Yes |
| B3LYP | 6-31G(d,p) | 0.30 | Medium | Yes |
| PBE0 | 6-311G(d,p) | 0.40 | Medium | Yes |
| M06-2X | 6-311+G(d,p) | 0.20 | High | Yes |
| wB97X-D | def2-TZVP | 0.10 | High | Yes |
| MP2 | aug-cc-pVTZ | 0.05 | Very High | Yes |
Molecular Dynamics Profiling of Protein-Ligand Stability
Molecular dynamics (MD) simulations provide essential insights into the temporal evolution of protein-ligand complexes, enabling the assessment of binding stability and conformational dynamics [18] [19]. These methodologies complement static quantum mechanical calculations by incorporating thermal motion and solvent effects that are crucial for realistic modeling of biological systems [20] [21].
Equilibrium Molecular Dynamics
Classical molecular dynamics simulations employ empirical force fields to model atomic interactions over timescales ranging from nanoseconds to microseconds [18] [19]. The integration of Newton's equations of motion enables the prediction of conformational changes and binding stability under physiological conditions [20] [21]. These simulations provide critical information about protein-ligand complex stability, with approximately 94% of native binding poses maintaining stability during equilibrium MD simulations [18] [19].
Advanced MD methodologies include steered molecular dynamics for non-equilibrium processes and umbrella sampling for free energy calculations [22] [23]. These techniques enable the investigation of binding and unbinding pathways, providing insights into the kinetic and thermodynamic aspects of protein-ligand interactions [22] [23]. The application of replica exchange molecular dynamics extends the accessible timescales by enhancing conformational sampling through temperature exchange protocols [20] [24].
Thermal Titration Molecular Dynamics
Thermal titration molecular dynamics (TTMD) represents an innovative approach for assessing protein-ligand complex stability through progressive temperature increases [20] [24]. This methodology evaluates binding mode conservation across temperature ranges from 300 K to 450 K, providing quantitative measures of complex stability [20] [24]. The TTMD protocol generates molecular stability (MS) coefficients that correlate with experimental binding affinities, enabling the discrimination between high-affinity and low-affinity compounds [20] [24].
The implementation of TTMD involves interaction fingerprint analysis to monitor binding mode conservation throughout the simulation [20] [24]. This approach provides a cost-effective alternative to computationally intensive free energy calculations while maintaining predictive accuracy [20] [24]. The methodology has demonstrated success across multiple pharmaceutical targets, including protein kinases and viral proteases [20] [24].
Free Energy Calculations
Free energy perturbation (FEP) and thermodynamic integration (TI) methods enable the quantitative prediction of binding affinities through rigorous statistical mechanical principles [22] [23]. These approaches require the definition of thermodynamic pathways connecting different chemical states, typically involving the gradual transformation of one ligand into another [22] [23]. The accuracy of free energy calculations depends critically on adequate phase space sampling and the choice of intermediate states along the transformation pathway [22] [23].
Advanced free energy methodologies incorporate enhanced sampling techniques to overcome conformational barriers and improve convergence [25] [26]. Temperature accelerated molecular dynamics and metadynamics approaches enable the exploration of rare events and conformational transitions [25] [26]. The integration of machine learning techniques with free energy calculations represents a promising direction for improving computational efficiency and accuracy [27] [28].
Table 2: Molecular Dynamics Simulation Types
| Simulation Type | Time Scale | Temperature Range (K) | Applications | Accuracy |
|---|---|---|---|---|
| Classical MD | ns-μs | 300 | Equilibrium | High |
| Steered MD | ps-ns | 300 | Non-equilibrium | Medium |
| Umbrella Sampling | ns-μs | 300 | Free energy | Very High |
| Replica Exchange | ns-μs | 300-400 | Conformational | High |
| Metadynamics | ns-μs | 300-400 | Rare events | Very High |
| TTMD | ns | 300-450 | Stability | High |
Machine Learning-Based Polypharmacology Risk Assessment
Machine learning methodologies have revolutionized polypharmacology research by enabling the prediction of multi-target drug interactions and the assessment of associated risks [29] [30]. These approaches leverage large-scale chemical and biological datasets to identify patterns and relationships that are not apparent through traditional computational methods [31] [32].
Drug-Target Interaction Prediction
Supervised machine learning algorithms, including random forest classifiers, support vector machines, and neural networks, have demonstrated remarkable success in predicting drug-target interactions [30] [31]. These methods utilize diverse molecular descriptors, including chemical fingerprints, pharmacophore features, and network topology parameters, to construct predictive models [30] [31]. The integration of multiple data types through ensemble methods enhances prediction accuracy and provides robust estimates of model uncertainty [30] [31].
Recent developments in deep learning have enabled the processing of complex molecular representations, including graph-based neural networks for chemical structures and sequence-based models for protein targets [29] [33]. These approaches achieve prediction accuracies exceeding 90% for well-validated datasets, representing significant improvements over traditional methods [29] [33]. The application of attention mechanisms and transformer architectures has further enhanced the interpretability of deep learning models [29] [33].
Polypharmacology Network Analysis
Network-based approaches to polypharmacology leverage graph theoretical methods to analyze drug-target interaction networks [34] [35]. These methodologies identify key nodes and pathways that mediate multi-target effects, providing insights into the mechanisms underlying polypharmacological activity [34] [35]. The integration of protein-protein interaction networks with drug-target associations enables the prediction of off-target effects and adverse drug reactions [34] [35].
Machine learning algorithms applied to network data include graph convolutional networks, random walks, and clustering methods [36] [37]. These techniques enable the identification of drug repurposing opportunities and the prediction of synergistic drug combinations [36] [37]. The incorporation of temporal dynamics into network models provides additional insights into the evolution of drug resistance and the development of combination therapies [36] [37].
Integration of Computational Approaches
The integration of quantum mechanical simulations, molecular dynamics, and machine learning represents the future of computational pharmacophore modeling [2] [4]. Hybrid quantum mechanics/molecular mechanics (QM/MM) approaches enable the accurate treatment of chemical reactions while maintaining computational efficiency for large biomolecular systems [2] [3]. The combination of these methodologies provides comprehensive insights into drug-target interactions across multiple scales [2] [4].
Machine learning acceleration of quantum mechanical calculations represents a particularly promising development, enabling the prediction of electronic properties with near-quantum accuracy at reduced computational cost [28] [39]. These approaches utilize neural network potentials trained on quantum mechanical data to perform large-scale molecular dynamics simulations [28] [39]. The integration of these methodologies is expected to transform drug discovery by enabling the rapid screening of large chemical libraries with quantum mechanical accuracy [28] [39].
Table 4: Pharmacophore Features and Properties
| Feature Type | Symbol | Geometric Shape | Interaction Energy (kcal/mol) | Distance Tolerance (Å) |
|---|---|---|---|---|
| Hydrogen Bond Acceptor | HBA | Sphere | 2-5 | ±1.0 |
| Hydrogen Bond Donor | HBD | Vector | 3-7 | ±1.2 |
| Hydrophobic | H | Sphere | 1-3 | ±1.5 |
| Aromatic | AR | Ring | 2-4 | ±1.0 |
| Positive Ionizable | PI | Sphere | 5-15 | ±1.0 |
| Negative Ionizable | NI | Sphere | 5-15 | ±1.0 |








