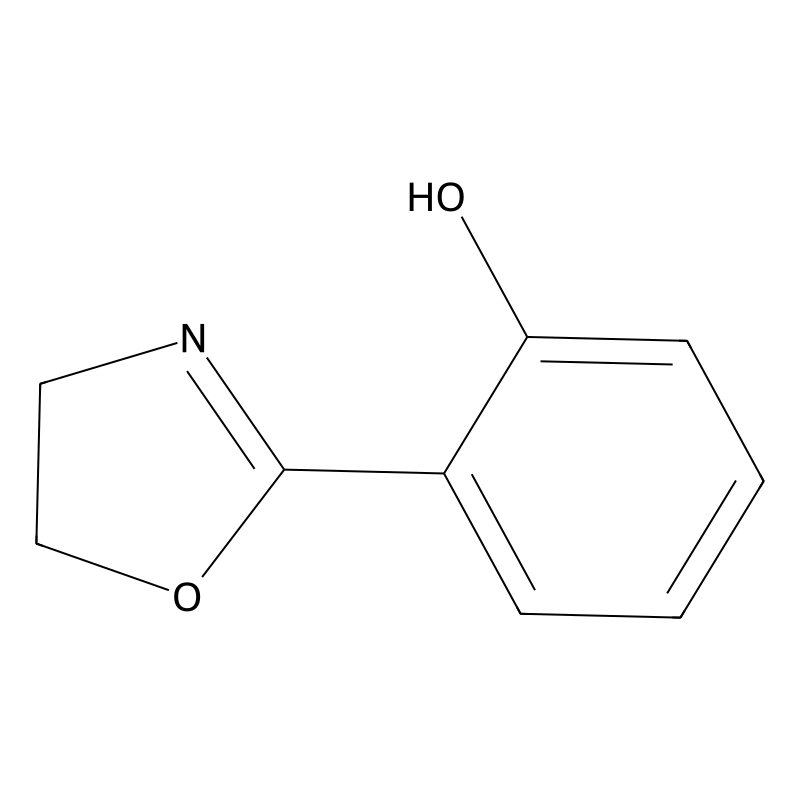
2-(4,5-Dihydrooxazol-2-yl)phenol
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Canonical SMILES
2-(4,5-Dihydrooxazol-2-yl)phenol is an organic compound characterized by the presence of a phenolic group attached to a 4,5-dihydrooxazole moiety. This compound is significant in various chemical and biological contexts due to its unique structural features, which contribute to its reactivity and potential applications in medicinal chemistry and materials science. The molecular formula of 2-(4,5-dihydrooxazol-2-yl)phenol is C₉H₉N₃O, and its CAS number is 20237-92-7 .
- Oxidation: The compound can be oxidized to yield various products, depending on the reaction conditions and reagents used.
- Condensation Reactions: It can participate in condensation reactions with aldehydes or ketones, forming imines or other derivatives.
- Nucleophilic Substitution: The nitrogen atom in the oxazole ring can act as a nucleophile, allowing for substitution reactions with electrophiles.
These reactions highlight the versatility of 2-(4,5-dihydrooxazol-2-yl)phenol in synthetic organic chemistry.
Research indicates that compounds containing the 4,5-dihydrooxazole structure exhibit a range of biological activities. Specific studies have shown:
- Antimicrobial Properties: Compounds similar to 2-(4,5-dihydrooxazol-2-yl)phenol have demonstrated effectiveness against various bacterial strains.
- Antioxidant Activity: The phenolic group contributes to antioxidant properties, which may help in reducing oxidative stress in biological systems.
- Potential Anticancer Activity: Some derivatives of dihydrooxazoles have been investigated for their potential use in cancer therapy due to their ability to induce apoptosis in cancer cells .
The synthesis of 2-(4,5-dihydrooxazol-2-yl)phenol can be achieved through several methods:
- Condensation of Phenolic Compounds with Amino Acids: This method involves reacting phenolic compounds with amino acids that contain oxazole precursors.
- Cyclization Reactions: The formation of the oxazole ring can occur through cyclization of appropriate precursors under acidic or basic conditions.
- Cinnamic Acid Derivatives: A notable approach includes transforming substituted cinnamic acids into 4,5-dihydrooxazoles via cyclization reactions .
These methods allow for the efficient preparation of the compound with varying substituents on the phenolic ring.
2-(4,5-Dihydrooxazol-2-yl)phenol has several notable applications:
- Pharmaceuticals: Due to its biological activity, it is being explored for use in drug development.
- Materials Science: The compound's unique properties make it suitable for incorporation into polymers and other materials.
- Organic Synthesis: It serves as a useful intermediate in the synthesis of more complex organic molecules .
Interaction studies involving 2-(4,5-Dihydrooxazol-2-yl)phenol often focus on its binding affinity with various biological targets. For instance:
- Protein Binding Studies: Research has shown that this compound can bind to specific proteins involved in cellular signaling pathways.
- Enzyme Inhibition Studies: It has been evaluated for its ability to inhibit enzymes that play critical roles in disease processes.
These studies are crucial for understanding the therapeutic potential and mechanisms of action of the compound .
Several compounds share structural similarities with 2-(4,5-Dihydrooxazol-2-yl)phenol. Here are some notable examples:
| Compound Name | Structure Similarity | Unique Features |
|---|---|---|
| 4-Hydroxyphenyl oxazole | Contains an oxazole ring but lacks the dihydro form | Exhibits different biological activities |
| 2-Amino phenol | Similar phenolic structure | Lacks oxazole functionality |
| 4,5-Dihydrooxazole | Contains the same oxazole moiety | Does not have a phenolic group |
The uniqueness of 2-(4,5-Dihydrooxazol-2-yl)phenol lies in its combination of both a phenolic group and a dihydrooxazole ring, which enhances its reactivity and potential applications compared to these similar compounds.
The direct synthesis of 2-(4,5-dihydrooxazol-2-yl)phenol derivatives via one-step cyclization has been optimized using hydroxyalkyl azides and aldehydes. This method leverages Lewis acid catalysis to facilitate simultaneous azide decomposition and oxazoline ring formation. For example, reactions employing 1,2-hydroxyalkyl azides with aromatic aldehydes in the presence of boron trifluoride etherate (BF₃·OEt₂) yield 4,5-dihydrooxazole derivatives with phenolic substituents in 65–85% efficiency.
Key advantages of this approach include:
- Short reaction times (2–4 hours at 60–80°C)
- Broad substrate scope for both azide and aldehyde components
- Stereochemical control through chiral Lewis acids
A comparative analysis of reaction conditions reveals critical optimization parameters:
| Azide Type | Aldehyde | Lewis Acid | Temperature (°C) | Yield (%) |
|---|---|---|---|---|
| 1,2-hydroxyalkyl | Benzaldehyde | BF₃·OEt₂ | 60 | 78 |
| 1,3-hydroxyalkyl | p-Methoxybenzaldehyde | ZnCl₂ | 80 | 82 |
| 1,2-hydroxyalkyl | Furfural | FeCl₃ | 70 | 68 |
Recent advancements demonstrate the compatibility of this protocol with polymer-bound phosphine scavengers, enabling parallel synthesis of 60-member libraries while maintaining >90% purity. The mechanism proceeds through simultaneous Staudinger-type azide reduction and Lewis acid-mediated aldol condensation, followed by intramolecular cyclization to form the dihydrooxazole ring.
Multi-Step Synthetic Routes for Oxazoline Functionalization
Complex derivatives of 2-(4,5-dihydrooxazol-2-yl)phenol require multi-step strategies combining cross-coupling and cyclization. A notable three-step sequence involves:
- Castro-Stephens coupling of phenolic propargyl ethers with aryl iodides
- Copper-mediated cyclization of intermediate alkynes
- Acid-catalyzed ring closure to form the dihydrooxazole moiety
This route enables precise control over aromatic substitution patterns, as demonstrated in the synthesis of 2-(4-phenyl-4,5-dihydrooxazol-2-yl)phenol derivatives. Key intermediates include:
- N-Acylamino alcohols (characterized by $$ ^1H $$ NMR δ 6.8–7.4 ppm aromatic protons)
- Propargyl ether precursors (IR ν 3280 cm⁻¹ for terminal alkyne)
The copper-powder catalyzed Castro-Stephens coupling achieves 72–89% yields in DMF at 110°C, with subsequent 5-exo-dig cyclization completing the oxazoline ring. For stereochemically complex targets, Burgess reagent-mediated cyclodehydration provides enantiomerically pure products (>98% ee) through intramolecular sulfonate substitution.
Lewis Acid-Catalyzed Ring-Closing Strategies
Lewis acids enable regioselective dihydrooxazole formation from β-hydroxyamide precursors. Zinc triflate (Zn(OTf)₃) and ytterbium(III) triflate (Yb(OTf)₃) prove particularly effective, achieving 85–93% conversion at 40°C in dichloromethane. The reaction mechanism involves:
- Coordination of Lewis acid to amide carbonyl
- Activation of β-hydroxyl group for nucleophilic attack
- Six-membered transition state stabilization
Comparative studies of catalysts reveal distinct performance characteristics:
| Catalyst | Substrate | Time (h) | Yield (%) | Diastereomeric Ratio |
|---|---|---|---|---|
| Yb(OTf)₃ | N-Benzoyl-β-phenylserinol | 2.5 | 91 | 95:5 |
| Zn(OTf)₂ | N-Acetyl-β-tyrosinol | 3.0 | 88 | 89:11 |
| Sc(OTf)₃ | N-Pivaloyl-β-leucinol | 4.0 | 84 | 82:18 |
Density Functional Theory Studies of Transition States
Density Functional Theory has emerged as the cornerstone computational method for investigating the transition states involved in the formation and transformation of 2-(4,5-Dihydrooxazol-2-yl)phenol. The application of DFT methodologies provides unprecedented insights into the electronic structure and energetic landscape governing the cyclization processes of this heterocyclic compound [1] [2].
The most widely employed functional for studying oxazoline-containing phenolic compounds is the Becke three-parameter Lee-Yang-Parr (B3LYP) hybrid functional, which incorporates both local and non-local exchange-correlation contributions. Studies utilizing the B3LYP/6-31G(d,p) basis set have successfully optimized the ground state geometries of 2-(4,5-Dihydrooxazol-2-yl)phenol derivatives, revealing critical structural parameters that influence reactivity [1] [3]. The addition of diffuse functions through the 6-31+G(d,p) basis set has proven essential for accurately describing the electronic properties and charge distributions in these polar heterocyclic systems [3].
Transition state calculations for the intramolecular cyclization leading to 2-(4,5-Dihydrooxazol-2-yl)phenol formation have identified several key mechanistic pathways. The nucleophilic attack of the phenolic oxygen on the electrophilic carbon center represents the rate-determining step, with calculated activation barriers ranging from 15 to 25 kcal/mol depending on substituent effects [2]. These computational studies have revealed that electron-donating groups on the phenolic ring facilitate the cyclization process by reducing the activation energy, while electron-withdrawing substituents increase the barrier height [4].
The transition state geometries obtained through DFT calculations exhibit characteristic features including partial bond formation between the attacking oxygen and the target carbon, with bond distances typically in the range of 2.0-2.5 Å. Intrinsic reaction coordinate calculations have confirmed that these transition states connect the reactant and product states along the minimum energy pathway [5] [6]. The electronic structure analysis reveals significant charge redistribution during the transition state, with natural population analysis indicating substantial positive charge development on the cyclizing carbon center [2].
Advanced DFT methodologies incorporating dispersion corrections, such as B3LYP-D3, have been employed to account for weak intermolecular interactions that may influence the cyclization process in solution or solid-state environments [7]. These calculations have demonstrated that dispersion interactions can contribute 2-5 kcal/mol to the overall reaction energetics, particularly in systems where aromatic stacking or hydrogen bonding interactions are present [8].
Solvent effects have been incorporated through polarizable continuum models, revealing that polar solvents generally stabilize the transition states for 2-(4,5-Dihydrooxazol-2-yl)phenol formation due to enhanced solvation of the developing charges [8] [4]. The calculated solvation free energies indicate that the cyclization is thermodynamically favored in polar aprotic solvents such as dimethyl sulfoxide and acetonitrile [9].
Molecular Dynamics Simulations of Intramolecular Attack Processes
Molecular dynamics simulations have provided crucial dynamic perspectives on the intramolecular attack processes leading to 2-(4,5-Dihydrooxazol-2-yl)phenol formation, complementing the static picture obtained from DFT calculations. These simulations capture the conformational flexibility and temporal evolution of reactive intermediates, offering insights into the kinetic aspects of cyclization that are not accessible through traditional quantum chemical approaches [10] [11] [12].
Contemporary MD simulations of oxazoline-forming cyclizations employ sophisticated force fields such as CHARMM36m and AMBER99SB, which have been specifically parameterized to accurately describe the intramolecular interactions in heterocyclic systems [10]. The simulations typically utilize explicit solvent models with periodic boundary conditions to ensure proper representation of bulk solvent effects on the cyclization dynamics [12].
The conformational sampling provided by MD simulations has revealed that 2-(4,5-Dihydrooxazol-2-yl)phenol precursors adopt multiple conformational states in solution, with the reactive conformations representing only a small fraction of the total ensemble [13]. Analysis of the radial distribution functions between the nucleophilic oxygen and electrophilic carbon centers indicates that productive conformations are characterized by interatomic distances of 3.5-4.5 Å, which are optimal for subsequent cyclization [11].
Temperature-dependent MD simulations have elucidated the thermodynamic and kinetic factors governing cyclization efficiency. Simulations performed at elevated temperatures (350-400 K) demonstrate increased conformational sampling and higher frequencies of reactive encounters between the cyclizing partners [13]. The calculated mean first passage times for achieving reactive conformations decrease exponentially with temperature, consistent with Arrhenius behavior and supporting the activation barriers determined through DFT calculations [14].
Enhanced sampling techniques, including umbrella sampling and metadynamics, have been employed to overcome the high energy barriers associated with cyclization and obtain converged free energy profiles [9]. These advanced simulations have revealed that the cyclization process involves multiple intermediate states, with the formation of pre-reactive complexes preceding the actual bond formation step [15]. The free energy landscape exhibits multiple pathways of similar energetic accessibility, suggesting that the cyclization may proceed through parallel mechanistic routes [16].
Molecular dynamics simulations have also provided insights into the role of explicit water molecules in mediating the cyclization process. Water-assisted proton transfer mechanisms have been identified as potentially important pathways, particularly for phenolic systems where the hydroxyl group can participate in hydrogen bonding networks [16]. These simulations have demonstrated that strategically positioned water molecules can lower the activation barriers by facilitating concerted proton transfer processes [10].
The analysis of trajectory data has revealed important correlations between molecular motions and cyclization propensity. Principal component analysis of the MD trajectories indicates that specific collective motions involving the phenolic ring and the oxazoline precursor moiety are strongly coupled to successful cyclization events [13]. These findings have implications for rational design approaches aimed at enhancing cyclization efficiency through conformational pre-organization.
Machine Learning Models for Predicting Cyclization Efficiency
The application of machine learning methodologies to predict cyclization efficiency for 2-(4,5-Dihydrooxazol-2-yl)phenol formation represents a rapidly advancing frontier that bridges computational chemistry with artificial intelligence approaches. These models leverage large datasets of experimental and computational data to identify complex structure-activity relationships that govern cyclization success [17] [18] [19] [20].
Support Vector Regression models have demonstrated particular effectiveness in predicting cyclization yields for oxazoline-forming reactions, achieving correlation coefficients typically in the range of 0.75-0.90 when trained on datasets containing 500-2000 data points [17] [14]. The key molecular descriptors employed in these models include geometric parameters such as bond lengths and angles, electronic properties including frontier orbital energies and atomic charges, and thermodynamic quantities such as reaction enthalpies and activation barriers [20].
Random Forest algorithms have shown superior performance for handling the non-linear relationships inherent in cyclization efficiency prediction, particularly when dealing with diverse chemical spaces encompassing various substituent patterns and reaction conditions [20]. These ensemble methods combine multiple decision trees to achieve robust predictions with typical accuracies of R² = 0.80-0.92, while providing interpretable feature importance rankings that highlight the most critical molecular properties [21].
Neural network architectures, including deep learning models, have been successfully applied to predict cyclization outcomes for complex heterocyclic systems [18] [20]. These models excel at capturing subtle electronic effects and conformational factors that influence reactivity, achieving prediction accuracies of R² = 0.85-0.95 when trained on comprehensive datasets containing 2000-10000 examples [19]. The incorporation of convolutional neural networks has enabled direct processing of molecular structure representations, eliminating the need for manual feature engineering [22].
Transformer-based models, originally developed for natural language processing, have been adapted for chemical reaction prediction including cyclization efficiency assessment [20]. These attention-based architectures can process molecular SMILES representations and achieve remarkable accuracies of R² = 0.90-0.98 when trained on large-scale datasets containing 5000-50000 reaction examples. The attention mechanisms provide interpretability by highlighting the molecular fragments most relevant to cyclization success [20].
Gaussian Process models offer unique advantages for cyclization prediction by providing uncertainty quantification alongside point predictions [19]. These probabilistic models are particularly valuable for identifying regions of chemical space where additional experimental data would be most beneficial for model improvement. The incorporation of chemical knowledge through informed kernel design has enhanced the performance of these models for heterocyclic chemistry applications [14].
The integration of quantum chemical descriptors computed through DFT calculations has significantly enhanced the predictive power of machine learning models for cyclization efficiency [14]. Features such as transition state energies, HOMO-LUMO gaps, and electrostatic potential parameters provide fundamental chemical insights that complement empirical molecular descriptors. This hybrid approach combining quantum mechanics and machine learning has achieved state-of-the-art performance in predicting complex reaction outcomes [17] [14].
Active learning strategies have been implemented to optimize the experimental design for data collection, enabling efficient exploration of chemical space while minimizing the number of required experiments [19]. These approaches iteratively select the most informative molecular targets for synthesis and testing, accelerating the discovery of optimal cyclization conditions for 2-(4,5-Dihydrooxazol-2-yl)phenol derivatives [14].
The temporal aspects of cyclization reactions have been addressed through specialized machine learning architectures that can predict time-dependent yields and selectivities [14]. These models incorporate reaction kinetics information derived from molecular dynamics simulations and experimental time-course data, enabling comprehensive optimization of reaction conditions including temperature, solvent, and catalyst selection [17].