Maclurin
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
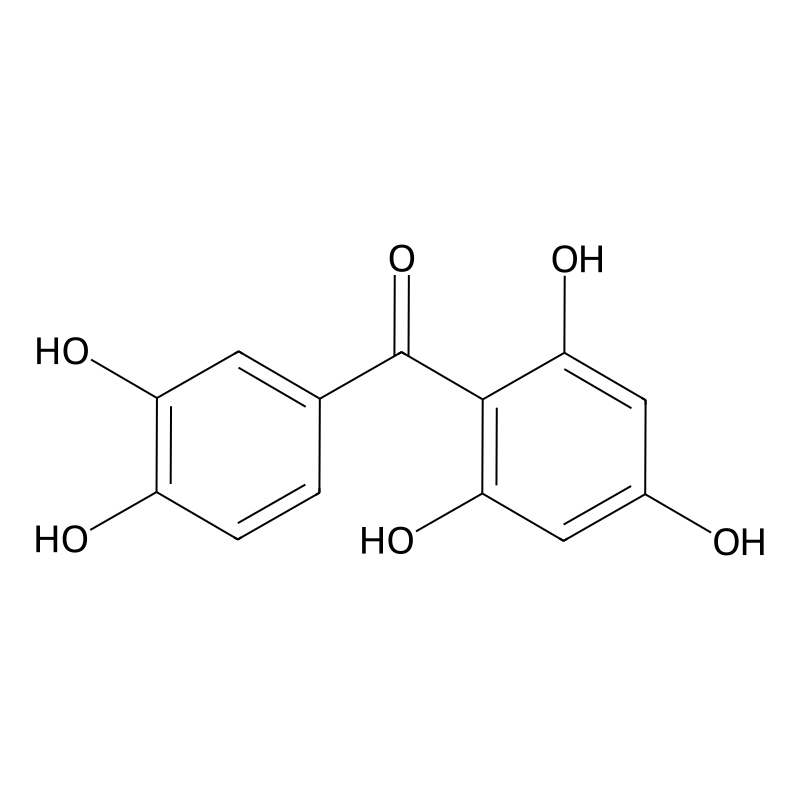
SMILES
solubility
Synonyms
Canonical SMILES
Approximating Complex Functions
Many functions encountered in scientific research are too complex to evaluate directly. Maclaurin series allows researchers to approximate the behavior of these functions by expressing them as an infinite sum of polynomials. By considering a finite number of terms from the series, researchers can obtain accurate approximations, often sufficient for practical purposes. This is particularly useful in fields like physics, engineering, and computational science where complex functions model real-world phenomena [].
For instance, calculating the sine function of an angle might be computationally expensive. However, the Maclaurin series for sine allows researchers to approximate the sine value with a high degree of accuracy using just a few terms, significantly reducing computational burden [].
Solving Differential Equations
Differential equations are a cornerstone of scientific modeling, describing the rate of change of a quantity. Maclaurin series plays a crucial role in solving certain types of differential equations. By expressing the solution as a Maclaurin series, researchers can obtain approximate or exact solutions depending on the specific equation. This is particularly valuable in areas like physics, chemistry, and biology, where differential equations model various phenomena like motion, reaction rates, and population growth [].
For example, the heat equation, which governs heat flow in a material, can be solved using a Maclaurin series approach, providing valuable insights into thermal behavior [].
Numerical Analysis and Computer Science
Maclaurin series is a powerful tool in numerical analysis, a subfield of mathematics concerned with developing efficient algorithms for solving problems. By approximating functions with Maclaurin series, researchers can design algorithms that perform calculations with a desired level of accuracy. This is crucial in computer science fields like computer graphics, where functions represent shapes, colors, and lighting effects [].
For instance, ray tracing algorithms, which generate realistic images in computer graphics, rely on Maclaurin series to represent the trajectories of light rays, contributing to the creation of visually stunning graphics [].
Maclurin is a naturally occurring compound classified as a flavonoid, specifically a type of polyphenol. It is primarily found in the fruit of the Morus alba (white mulberry) and is recognized for its diverse biological activities, particularly its antioxidant and anti-melanogenic properties. Structurally, maclurin is characterized by its phenolic hydroxyl groups, which contribute to its reactivity and biological effects. The compound has gained attention for its potential therapeutic applications, especially in dermatology and cancer treatment.
The biological activities of maclurin are extensive:
- Antioxidant Activity: Maclurin effectively scavenges free radicals, protecting cells from oxidative stress. Studies have shown that it can enhance the antioxidant capacity of cells and tissues, outperforming even well-known antioxidants like vitamin C .
- Anti-Melanogenic Effects: Maclurin promotes melanogenesis through the activation of specific signaling pathways (cAMP/PKA/CREB and p38 MAPK), increasing the expression of proteins involved in melanin production such as microphthalmia-associated transcription factor (MITF) and tyrosinase-related proteins .
- Cytoprotection: It has been demonstrated that maclurin protects melanocytes from oxidative damage induced by hydrogen peroxide and ultraviolet radiation .
Maclurin can be synthesized through various methods:
- Extraction from Natural Sources: The most common method involves extracting maclurin from the fruit of Morus alba using solvents like ethanol or methanol. This method preserves the compound's natural structure and activity.
- Chemical Synthesis: Synthetic approaches may involve the modification of simpler flavonoid structures through
Maclurin has several promising applications:
- Cosmetic Industry: Due to its anti-melanogenic properties, maclurin is being explored as an ingredient in skin-lightening products and formulations aimed at treating hyperpigmentation disorders.
- Pharmaceuticals: Its antioxidant properties make maclurin a candidate for developing drugs aimed at combating oxidative stress-related diseases, including cancer and neurodegenerative disorders.
- Food Industry: As a natural preservative, maclurin can be used to prevent browning in food products due to its antioxidant activity.
Research into the interactions of maclurin with biological targets has highlighted its potential therapeutic benefits:
- Tyrosinase Inhibition: Studies have shown that maclurin binds effectively to tyrosinase, suggesting it could be used as a natural alternative to synthetic tyrosinase inhibitors in cosmetic formulations .
- Cellular Signaling Pathways: Maclurin activates key signaling pathways involved in melanogenesis, indicating its role in regulating skin pigmentation at a molecular level .
Several compounds share structural similarities with maclurin, each exhibiting unique properties:
| Compound | Source | Biological Activity | Unique Features |
|---|---|---|---|
| Kojic Acid | Fungi | Tyrosinase inhibition | Widely used in skin-lightening products |
| Arbutin | Bearberry | Tyrosinase inhibition | Glycosylated form of hydroquinone |
| Resveratrol | Grapes | Antioxidant, anti-inflammatory | Known for cardiovascular benefits |
| Curcumin | Turmeric | Anti-inflammatory, antioxidant | Broad-spectrum health benefits |
Maclurin stands out due to its dual action as both an antioxidant and a modulator of melanin synthesis through specific signaling pathways, making it particularly valuable in dermatological applications.
The biosynthetic foundation of maclurin originates from central carbon metabolism through the convergence of two key precursor molecules: phosphoenolpyruvate (PEP) from glycolysis and erythrose 4-phosphate (E4P) from the pentose phosphate pathway [5] [6]. These fundamental metabolites enter the shikimate pathway, which represents the exclusive route for chorismate biosynthesis in bacteria, fungi, algae, and plants, notably absent in animals [5] [7].
The initiation of this pathway occurs through the enzyme 3-deoxy-D-arabino-heptulosonate-7-phosphate synthase (DAHP synthase), which catalyzes the condensation of PEP and E4P to form 3-deoxy-D-arabino-heptulosonate-7-phosphate [6] [4]. In Arabidopsis thaliana, multiple DAHP synthase isoforms exist, with AtDAHPS1 requiring manganese ions and reduced thioredoxin for activity, thereby linking carbon flow into aromatic metabolism with photosynthetic electron transport [4]. This connection establishes a direct relationship between photosynthetic activity and the availability of precursors for maclurin biosynthesis.
The shikimate pathway proceeds through seven enzymatic steps, systematically converting the initial seven-carbon sugar phosphate through a series of cyclization, dehydration, reduction, and phosphorylation reactions [8] [9]. Key intermediates include 3-dehydroquinate, 3-dehydroshikimate, shikimate, shikimate 3-phosphate, and 5-enolpyruvylshikimate 3-phosphate, ultimately culminating in chorismate formation [6] [7]. Each step represents a potential regulatory point for controlling flux toward aromatic metabolites, including maclurin precursors.
The pathway demonstrates remarkable evolutionary conservation across diverse organisms while maintaining species-specific regulatory mechanisms [10] [11]. In plants, the entire shikimate pathway localizes primarily within plastids, distinguishing it from the cytoplasmic localization observed in microorganisms [6] [11]. This compartmentalization ensures efficient coupling with photosynthetic carbon fixation and provides spatial organization for subsequent aromatic amino acid biosynthesis.
Enzymatic Conversion Processes
The transformation of shikimate pathway intermediates into maclurin involves a complex network of enzymatic conversions that bridge primary and secondary metabolism [3] [4]. Chorismate serves as the central branch point metabolite, representing the terminal product of the shikimate pathway and the initial substrate for aromatic amino acid biosynthesis [3] [11]. From chorismate, three distinct pathways lead to the aromatic amino acids phenylalanine, tyrosine, and tryptophan, each serving as potential precursors for benzophenone derivatives like maclurin [4] [12].
The conversion of chorismate to prephenate through chorismate mutase represents the committed step toward phenylalanine and tyrosine biosynthesis [3] [13]. Multiple chorismate mutase isoforms exist in plants, each exhibiting distinct regulatory properties and subcellular localizations. In Arabidopsis, AtCM1 and AtCM3 contain plastid targeting sequences and demonstrate allosteric regulation by aromatic amino acids, while AtCM2 functions as a non-allosteric cytosolic enzyme [3]. These isoforms provide fine-tuned control over carbon flow into aromatic amino acid pools that may serve as maclurin precursors.
Prephenate undergoes conversion to either phenylpyruvate via prephenate dehydratase or 4-hydroxyphenylpyruvate through prephenate dehydrogenase, leading to phenylalanine and tyrosine respectively [14] [15]. The subsequent transamination reactions involve aromatic aminotransferases that utilize 2-ketoglutarate as the amino donor, connecting aromatic amino acid biosynthesis with nitrogen metabolism [14] [16]. These amino acids may then undergo further modifications through the phenylpropanoid pathway, which represents a major route for phenolic compound biosynthesis in plants [17] [18].
The specific enzymatic steps leading from aromatic amino acids to maclurin likely involve hydroxylation reactions catalyzed by cytochrome P450 enzymes, methylation by S-adenosyl methionine-dependent methyltransferases, and potential condensation reactions forming the characteristic benzophenone structure [19] [20]. Research on related compounds suggests that maclurin biosynthesis may proceed through hydroxylation of simpler benzophenone precursors, potentially involving iriflophenone as an intermediate derived from p-coumarate [20]. However, the complete enzymatic pathway from aromatic amino acids to maclurin remains incompletely characterized.
Localization in Plant Tissues
The tissue-specific distribution of maclurin reflects both its biosynthetic origins and functional roles within plant systems [2] [21]. Maclurin demonstrates highest concentrations in root bark tissues, where it serves as a stored defense compound and contributes to the plant's phenolic reserves [21] [22]. The root bark represents a primary site for maclurin accumulation, with concentrations significantly exceeding those found in other plant organs [23] [24].
Stem tissues, particularly young twigs, contain moderate to high levels of maclurin and related benzophenone derivatives [23]. Analysis of Morus alba twigs reveals that maclurin distribution varies with tissue age, harvest timing, and environmental conditions [23]. Young twigs harvested in early September show higher maclurin content compared to those collected in early July, suggesting seasonal regulation of biosynthesis or accumulation [23]. The presence of maclurin in stem tissues correlates with structural support functions and pathogen resistance mechanisms.
Leaf tissues exhibit variable maclurin content, generally lower than bark concentrations but sufficient to contribute to antioxidant activities and ultraviolet protection [21] [25]. The phenolic profile of Morus alba leaves includes multiple compounds related to maclurin biosynthesis, with chlorogenic acid representing the most abundant phenolic constituent [25]. Leaf-based maclurin content demonstrates cultivar-dependent variation and responds to environmental stresses, suggesting adaptive regulation of phenolic metabolism.
Vascular tissues show particular association with maclurin and related compounds, likely reflecting their role in lignification processes and transport regulation [26]. The localization of phenolic compounds within vascular elements supports both structural integrity and defense against vascular pathogens [21] [22]. Cell culture studies demonstrate that maclurin production can be maintained in suspension cultures under appropriate conditions, indicating that the biosynthetic machinery remains functional in dedifferentiated tissues [27].
Purity
Physical Description
XLogP3
Hydrogen Bond Acceptor Count
Hydrogen Bond Donor Count
Exact Mass
Monoisotopic Mass
Heavy Atom Count
Appearance
Melting Point
Storage
UNII
GHS Hazard Statements
H319 (100%): Causes serious eye irritation [Warning Serious eye damage/eye irritation];
H400 (100%): Very toxic to aquatic life [Warning Hazardous to the aquatic environment, acute hazard];
Information may vary between notifications depending on impurities, additives, and other factors. The percentage value in parenthesis indicates the notified classification ratio from companies that provide hazard codes. Only hazard codes with percentage values above 10% are shown.
Pictograms


Irritant;Environmental Hazard
Other CAS
Wikipedia
General Manufacturing Information
Dates
2: Ku MJ, Kim JH, Lee J, Cho JY, Chun T, Lee SY. Maclurin suppresses migration and invasion of human non-small-cell lung cancer cells via anti-oxidative activity and inhibition of the Src/FAK-ERK-β-catenin pathway. Mol Cell Biochem. 2015 Apr;402(1-2):243-52. doi: 10.1007/s11010-015-2331-4. Epub 2015 Jan 29. PubMed PMID: 25630491.
3: Healey M. Note on the supposed production of maclurin from acacatechin. Biochem J. 1932;26(2):388-91. PubMed PMID: 16744836; PubMed Central PMCID: PMC1260917.
4: Kaya D, Jäger AK, Yalçin FN, Ersöz T. MAO-A inhibition profiles of some benzophenone glucosides from Gentiana verna subsp. pontica. Nat Prod Commun. 2014 Apr;9(4):505-6. PubMed PMID: 24868869.
5: Kokotkiewicz A, Luczkiewicz M, Pawlowska J, Luczkiewicz P, Sowinski P, Witkowski J, Bryl E, Bucinski A. Isolation of xanthone and benzophenone derivatives from Cyclopia genistoides (L.) Vent. (honeybush) and their pro-apoptotic activity on synoviocytes from patients with rheumatoid arthritis. Fitoterapia. 2013 Oct;90:199-208. doi: 10.1016/j.fitote.2013.07.020. Epub 2013 Aug 3. PubMed PMID: 23916580.
6: Kumar V, Sood H, Chauhan RS. Detection of intermediates through high-resolution mass spectrometry for constructing biosynthetic pathways for major chemical constituents in a medicinally important herb, Swertia chirayita. Nat Prod Res. 2015;29(15):1449-55. doi: 10.1080/14786419.2015.1004175. Epub 2015 Jan 27. PubMed PMID: 25622657.
7: Xu YJ, Luo F, Gao Q, Shang Y, Wang C. Metabolomics reveals insect metabolic responses associated with fungal infection. Anal Bioanal Chem. 2015 Jun;407(16):4815-21. doi: 10.1007/s00216-015-8648-8. Epub 2015 Apr 21. PubMed PMID: 25895944.
8: Abdallah HM, El-Bassossy HM, Mohamed GA, El-Halawany AM, Alshali KZ, Banjar ZM. Phenolics from Garcinia mangostana alleviate exaggerated vasoconstriction in metabolic syndrome through direct vasodilatation and nitric oxide generation. BMC Complement Altern Med. 2016 Sep 13;16:359. doi: 10.1186/s12906-016-1340-5. PubMed PMID: 27618982; PubMed Central PMCID: PMC5020522.
9: Beelders T, de Beer D, Stander MA, Joubert E. Comprehensive phenolic profiling of Cyclopia genistoides (L.) Vent. by LC-DAD-MS and -MS/MS reveals novel xanthone and benzophenone constituents. Molecules. 2014 Aug 7;19(8):11760-90. doi: 10.3390/molecules190811760. PubMed PMID: 25105916.
10: Fromentin Y, Grellier P, Wansi JD, Lallemand MC, Buisson D. Yeast-mediated xanthone synthesis through oxidative intramolecular cyclization. Org Lett. 2012 Oct 5;14(19):5054-7. doi: 10.1021/ol302283p. Epub 2012 Sep 17. PubMed PMID: 22984826.
11: Hearn MT, Smith PK, Mallia AK. Isolation of the Maclura pomifera hemagglutinin on a deoxymelibiotol affinity support and preliminary characterization by buffer electrofocusing and high-performance liquid chromatography. Biosci Rep. 1982 Apr;2(4):247-55. PubMed PMID: 6896160.
12: Sugimori H, Ookuma Y, Iwasaka T. Immunohistochemical properties of the endometrial and cervical adenocarcinoma. Nihon Sanka Fujinka Gakkai Zasshi. 1986 Dec;38(12):2287-8. PubMed PMID: 2433372.
13: Lee SY. Synergistic effect of maclurin on ginsenoside compound K induced inhibition of the transcriptional expression of matrix metalloproteinase-1 in HaCaT human keratinocyte cells. J Ginseng Res. 2018 Apr;42(2):229-232. doi: 10.1016/j.jgr.2017.11.003. Epub 2017 Nov 21. PubMed PMID: 29719471; PubMed Central PMCID: PMC5925616.
14: Ajila CM, Rao LJ, Rao UJ. Characterization of bioactive compounds from raw and ripe Mangifera indica L. peel extracts. Food Chem Toxicol. 2010 Dec;48(12):3406-11. doi: 10.1016/j.fct.2010.09.012. Epub 2010 Sep 21. PubMed PMID: 20851730.
15: Chiang YM, Kuo YH, Oota S, Fukuyama Y. Xanthones and benzophenones from the stems of Garcinia multiflora. J Nat Prod. 2003 Aug;66(8):1070-3. PubMed PMID: 12932126.
16: Allen PZ. Interaction of Salmonella telaviv with Maclura pomifera lectin. Infect Immun. 1985 Jan;47(1):90-3. PubMed PMID: 3838092; PubMed Central PMCID: PMC261475.
17: Chang LW, Juang LJ, Wang BS, Wang MY, Tai HM, Hung WJ, Chen YJ, Huang MH. Antioxidant and antityrosinase activity of mulberry (Morus alba L.) twigs and root bark. Food Chem Toxicol. 2011 Apr;49(4):785-90. doi: 10.1016/j.fct.2010.11.045. Epub 2010 Dec 3. PubMed PMID: 21130832.
18: Imamura Y, Sugihara H, Miyake T, Ikeda T, Noriki S, Miyoshi N, Nakanishi K, Fukuda M. Lectin histochemistry in rat thyroid tumours. Basic Appl Histochem. 1989;33(3):185-96. PubMed PMID: 2818422.
19: Weller NK, Karnovsky MJ. Isolation of pulmonary alveolar type I cells from adult rats. Am J Pathol. 1986 Sep;124(3):448-56. PubMed PMID: 2945439; PubMed Central PMCID: PMC1888347.
20: Rooney SA, Gobran LI, Umstead TM, Phelps DS. Secretion of surfactant protein A from rat type II pneumocytes. Am J Physiol. 1993 Dec;265(6 Pt 1):L586-90. PubMed PMID: 8279574.