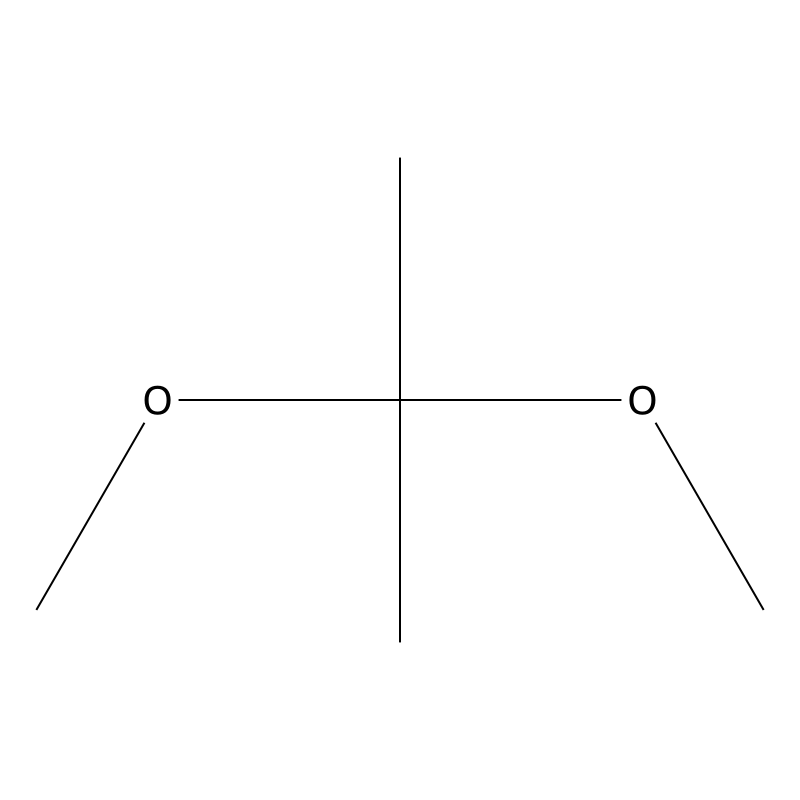
2,2-Dimethoxypropane
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Synonyms
Canonical SMILES
2,2-Dimethoxypropane (CAS 77-76-9) is a versatile, low-boiling (83 °C) organic reagent primarily procured as a highly efficient acetalization agent and chemical water scavenger [1]. Unlike passive desiccants, DMP reacts quantitatively with water under mild acid catalysis to generate acetone and methanol in an endothermic process [2]. This dual functionality makes it a critical raw material for the protection of 1,2- and 1,3-diols (acetonide formation), the synthesis of enol ethers such as 2-methoxypropene, and the driving of moisture-sensitive equilibria like esterifications[3]. Its ability to chemically consume water at room temperature eliminates the need for harsh thermal dehydration, making it a preferred choice for processing temperature-sensitive pharmaceutical intermediates and enabling rapid histological sample preparation [4].
References
- [1] Critchfield, F. E.; Bishop, E. T. 'Water determination by reaction with 2, 2-dimethoxypropane'. Anal. Chem. 1961.
- [2] Lorette, N.; Brown, Jr., J. 'Notes- Use of Acetone Dimethyl Acetal in Preparation of Methyl Esters'. J. Org. Chem. 1959.
- [3] Hubschwerlen, C.; Specklin, J.; Higelin, J. 'L-(S)-glyceraldehyde Acetonide'. Org. Synth. 1995.
- [4] Prentø, P. 'Rapid dehydration--clearing with 2,2-dimethoxypropane for paraffin embedding'. J. Histochem. Cytochem. 1978.
Substituting 2,2-Dimethoxypropane with standard physical water removal methods (e.g., Dean-Stark traps, molecular sieves) or alternative reagents (e.g., direct acetone, trimethyl orthoformate) often results in process bottlenecks [1]. Physical water removal requires elevated temperatures and extended reaction times, which can degrade sensitive substrates and increase energy costs during scale-up [2]. Direct condensation with acetone to form acetonides is thermodynamically limited by water accumulation, necessitating continuous azeotropic distillation that is difficult to implement in standard batch reactors [3]. While trimethyl orthoformate is a potent chemical water scavenger, it generates formate byproducts that can complicate downstream purification [4]. DMP circumvents these issues by irreversibly consuming water to form easily volatile byproducts (acetone and methanol), enabling rapid, high-yield conversions under mild, strictly anhydrous conditions without specialized distillation equipment [1].
References
- [1] Lorette, N.; Brown, Jr., J. 'Notes- Use of Acetone Dimethyl Acetal in Preparation of Methyl Esters'. J. Org. Chem. 1959.
- [2] Rodriguez et al. 'Selective esterification of aliphatic carboxyl groups'. Tetrahedron Lett. 1998.
- [3] Hubschwerlen, C.; Specklin, J.; Higelin, J. 'L-(S)-glyceraldehyde Acetonide'. Org. Synth. 1995.
- [4] Gopalsamuthiram, V., et al. 'A Concise Route to MK-4482 (EIDD-2801) from Cytidine: Part 2.' Synlett, 2021.
Accelerated Chemical Dehydration in Histology and Microscopy
In biological sample preparation, DMP provides a rapid chemical dehydration alternative to conventional physical solvent displacement. Studies demonstrate that acidified DMP can fully dehydrate tissue samples in 5 to 75 minutes, whereas standard graduated ethanol or acetone series require several days of sequential exchanges [1]. This is achieved through the quantitative, acid-catalyzed reaction of DMP with free water in the tissue, forming acetone and methanol in a single step without causing cellular collapse or requiring large solvent volumes[2].
| Evidence Dimension | Dehydration time for biological samples |
| Target Compound Data | 5 to 75 minutes (single step) |
| Comparator Or Baseline | Ethanol/acetone gradient series (several days, multi-step) |
| Quantified Difference | >95% reduction in processing time |
| Conditions | Acidified DMP vs. graduated solvent series at room temperature |
Enables high-throughput histological processing and significantly reduces solvent consumption and labor costs in microscopy workflows.
High-Yield Diol Protection via Thermodynamic Shifting
For the protection of vicinal diols, DMP acts as both the acetone source and a chemical water sink. Compared to direct condensation with acetone, which often stalls due to water accumulation, DMP drives the equilibrium forward by converting trace water into methanol and additional acetone [1]. This allows acetonide formation to proceed to >90% yield within hours under mild catalytic conditions (e.g., p-TsOH), avoiding the need for continuous azeotropic water removal [2].
| Evidence Dimension | Reaction efficiency and equipment requirements for 1,2-diol protection |
| Target Compound Data | >90% yield in hours under mild conditions without distillation |
| Comparator Or Baseline | Direct acetone condensation (requires continuous azeotropic distillation) |
| Quantified Difference | Elimination of thermal azeotropic distillation requirement with comparable or higher yields |
| Conditions | Acid-catalyzed acetalization at room temperature to mild reflux |
Simplifies the synthesis of complex pharmaceutical intermediates by enabling one-pot, mild-condition protection steps without specialized distillation equipment.
Mild-Condition Esterification via Chemical Water Scavenging
In the synthesis of methyl esters from carboxylic acids, the presence of water limits conversion. Utilizing DMP as an in situ water scavenger allows the reaction to achieve >95% yield at or near room temperature[1]. This contrasts sharply with traditional Dean-Stark methods, which require refluxing high-boiling solvents (e.g., toluene) for extended periods to physically remove water [2]. DMP's quantitative reaction with water ensures strictly anhydrous conditions, protecting thermally labile substrates from degradation.
| Evidence Dimension | Temperature conditions required for >95% esterification yield |
| Target Compound Data | Room temperature to mild heating (e.g., 25-40 °C) with DMP |
| Comparator Or Baseline | Dean-Stark apparatus (refluxing toluene/benzene, >80-110 °C) |
| Quantified Difference | >60 °C reduction in processing temperature |
| Conditions | Acid-catalyzed esterification of carboxylic acids |
Reduces energy consumption and thermal degradation risks during the scale-up of sensitive esterification processes.
Large-Scale Synthesis of Pharmaceutical Intermediates (Acetonides)
DMP is the reagent of choice for protecting 1,2- and 1,3-diols in complex API synthesis (e.g., nucleoside analogs, carbohydrates). Its ability to drive reactions to completion without azeotropic distillation simplifies reactor setup and improves batch-to-batch reproducibility [1].
High-Throughput Histological and Electron Microscopy Processing
In pathology and research laboratories, acidified DMP replaces multi-day ethanol gradient protocols for tissue dehydration. Its single-step chemical dehydration drastically reduces turnaround times for paraffin embedding and electron microscopy preparation [2].
Mild-Condition Esterification of Thermally Labile Compounds
For the production of specialty esters where substrates cannot tolerate the high temperatures of a Dean-Stark trap, DMP serves as an ideal in situ water scavenger, enabling high conversions at ambient temperatures [3].
Moisture-Sensitive Organometallic and Coupling Reactions
DMP is utilized to chemically dry solvents and reagents in situ prior to highly moisture-sensitive reactions (e.g., Grignard additions), ensuring strictly anhydrous conditions and preventing costly batch failures[4].
References
- [1] Gopalsamuthiram, V., et al. 'A Concise Route to MK-4482 (EIDD-2801) from Cytidine: Part 2.' Synlett, 2021.
- [2] Prentø, P. 'Rapid dehydration--clearing with 2,2-dimethoxypropane for paraffin embedding'. J. Histochem. Cytochem. 1978.
- [3] Lorette, N.; Brown, Jr., J. 'Notes- Use of Acetone Dimethyl Acetal in Preparation of Methyl Esters'. J. Org. Chem. 1959.
- [4] Critchfield, F. E.; Bishop, E. T. 'Water determination by reaction with 2, 2-dimethoxypropane'. Anal. Chem. 1961.
XLogP3
Boiling Point
Melting Point
UNII
GHS Hazard Statements
Reported as not meeting GHS hazard criteria by 5 of 196 companies. For more detailed information, please visit ECHA C&L website;
Of the 18 notification(s) provided by 191 of 196 companies with hazard statement code(s):;
H225 (100%): Highly Flammable liquid and vapor [Danger Flammable liquids];
H315 (54.97%): Causes skin irritation [Warning Skin corrosion/irritation];
H319 (99.48%): Causes serious eye irritation [Warning Serious eye damage/eye irritation];
Information may vary between notifications depending on impurities, additives, and other factors. The percentage value in parenthesis indicates the notified classification ratio from companies that provide hazard codes. Only hazard codes with percentage values above 10% are shown.
Vapor Pressure
Pictograms
Flammable;Irritant
Other CAS
Wikipedia
General Manufacturing Information
Dates
Preparation and synthetic application of partially protected brassinosteroids
Vladimir A Khripach, Vladimir N Zhabinskii, Yuliya Y Zhiburtovich, Galina V Ivanova, Olga V Konstantinova, Dmitrii V Tsavlovskii, Sybille Lorenz, Bernd SchneiderPMID: 19786042 DOI: 10.1016/j.steroids.2009.09.010
Abstract
Preparation of partially protected brassinosteroids is achieved through the reaction of the source material (24-epicastasterone and 24-epibrassinolide) with diol-specific reagents (2,2-dimethoxypropane and methylboronic acid). The obtained products were shown to be useful synthetic intermediates for further preparation of minor representatives of this class of natural phytohormones (such as 3,24-diepicastasterone and 3-dehydro-24-epibrassinolide).Determination of dimethyl sulfoxide and dimethyl sulfone in urine by gas chromatography-mass spectrometry after preparation using 2,2-dimethoxypropane
Akito Takeuchi, Shinobu Yamamoto, Rie Narai, Manami Nishida, Mikio Yashiki, Norihiro Sakui, Akira NameraPMID: 19688817 DOI: 10.1002/bmc.1313
Abstract
A method for routinely determination of dimethyl sulfoxide (DMSO) and dimethyl sulfone (DMSO(2)) in human urine was developed using gas chromatography-mass spectrometry. The urine sample was treated with 2,2-dimethoxypropane (DMP) and hydrochloric acid for efficient removal of water, which causes degradation of the vacuum level in mass spectrometer and shortens the life-time of the column. Experimental DMP reaction parameters, such as hydrochloric acid concentration, DMP-urine ratio, reaction temperature and reaction time, were optimized for urine. Hexadeuterated DMSO was used as an internal standard. The recoveries of DMSO and DMSO(2) from urine were 97-104 and 98-116%, respectively. The calibration curves showed linearity in the range of 0.15-54.45 mg/L for DMSO and 0.19-50.10 mg/L for DMSO(2). The limits of detection of DMSO and DMSO(2) were 0.04 and 0.06 mg/L, respectively. The relative standard deviations of intra-day and inter-day were 0.2-3.4% for DMSO and 0.4-2.4% for DMSO(2). The proposed method may be useful for the biological monitoring of workers exposed to DMSO in their occupational environment.Preparation of serial sections of arthropods using 2,2-dimethoxypropane dehydration and epoxy resin embedding under vacuum
A Pernstich, H W Krenn, G PassPMID: 12713135 DOI: 10.1080/10520290312120002
Abstract
Improved methods are described for anatomical investigation of small insects and other arthropods using serial semithin sections. The specimens were dehydrated with acidified 2,2-dimethoxypropane and embedded in ERL 4206 epoxy resin under vacuum. This procedure ensures good resin impregnation of thin, long body compartments and appendages. Furthermore, it produces excellent overall preservation of the specimen and its fragile anatomical structures. This procedure saves time and gives excellent results when sectioning difficult arthropod material. A continuous recording of serial semithin sections is possible when diamond knives are used.Direct methyl esterification with 2,2-dimethoxypropane for the simultaneous determination of urinary metabolites of toluene, xylene, styrene, and ethylbenzene by gas chromatography-mass spectrometry
Akito Takeuchi, Akira Namera, Norihiro Sakui, Shinobu Yamamoto, Kenji Yamamuro, Osamu Nishinoiri, Yoko Endo, Ginji EndoPMID: 30698338 DOI: 10.1002/1348-9585.12026
Abstract
The purpose of this study was to develop a simple and accurate gas chromatography-mass spectrometry (GC-MS) method for simultaneous determination of four urinary metabolites from four organic solvents, that is, hippuric acid (HA) from toluene, methylhippuric acid (MHA) from xylene, and mandelic acid (MA) and phenylglyoxylic acid (PGA) from styrene or ethylbenzene for biological monitoring.The four metabolites were directly methyl-esterified with 2,2-dimethoxypropane and analyzed using GC-MS. The proposed method was validated according to the US Food and Drug Administration guidance. The accuracy of the proposed method was confirmed by analyzing a ClinChek
-Control for occupational medicine (RECIPE Chemicals +Instruments GmbH).
Calibration curves showed linearity in the concentration range of 10-1000 mg/L for each metabolite, with correlation coefficients >0.999. For each metabolite, the limits of detection and quantification were 3 mg/L and 10 mg/L, respectively. The recovery was 93%-117%, intraday accuracy, expressed as the deviation from the nominal value, was 92.7%-103.0%, and intraday precision, expressed as the relative standard deviation (RSD), was 1.3%-4.7%. Interday accuracy and precision were 93.4%-104.0% and 1.2%-9.5%, respectively. The analytical values of ClinChek obtained using the proposed method were sufficiently accurate.
The proposed method is a simple and accurate which is suitable for routine analyses that could be used for biological monitoring of occupational exposure to four organic solvents.
Matrix isolation infrared and ab initio study of the conformations of 2,2-dimethoxypropane
V Venkatesan, K Sundararajan, K S ViswanathanPMID: 12714073 DOI: 10.1016/s1386-1425(02)00358-x
Abstract
Conformations of 2,2-dimethoxypropane (DMP) were studied using matrix isolation infrared spectroscopy. An effusive source maintained at different temperatures (298, 388 and 430 K) was used to deposit DMP in a nitrogen matrix. As a result of these experiments, spectrally resolved infrared features of the ground and first higher energy conformer of DMP have been recorded, for the first time. The experimental studies were supported by ab initio computations performed at B3LYP/6-31++G** level. Computationally, four minima were identified corresponding to conformers with G+/-G-/+, TG+/-, G+/-G+/- and TT structures. The computed frequencies at the B3LYP level were found to compare well with the experimental matrix isolation frequencies, leading to a definitive assignment of the infrared features of DMP, for the G+/-G-/+ and TG+/- conformers. At the B3LYP/6-31++G** level, the energy difference between the G+/-G-/+ and TG+/- conformers was computed to be 3.25 kcal x mol(-1). The barrier for conformation interconversion, TG+/--->G+/-G-/+, was calculated to be 1.29 kcal x mol(-1). The magnitude of this barrier is consistent with the experimental observation that the spectral features due to the TG+/- decreased considerably in intensity when the matrix was annealed.Chemical dehydration of specimens with 2,2-dimethoxypropane (DMP) for paraffin processing of animal tissues: practical and economic advantages over dehydration in ethanol
K Conway, J A KiernanPMID: 10190257 DOI: 10.3109/10520299909066473
Abstract
Chemical dehydration can be accomplished using 2,2-dimethoxypropane (DMP). In the presence of an acid catalyst, this liquid reacts with water generating methanol and acetone as products. Although DMP is more expensive per milliliter than ethanol and other solvents used for dehydration, it is an economical alternative because a much smaller volume is needed. Slow penetration of DMP was previously thought to restrict its use to tiny specimens, but we now show that pieces of tissue as thick as 2 cm are dehydrated by overnight immersion in acidified DMP. We also show that dehydration in acidified DMP does not impair the staining of RNA or other basophilic components of animal tissues. The temperature and concentrations of methanol and H+ in the chemical dehydrating agent are too low to produce histochemically detectable methylation or nucleic acid extraction.Preparing living pollen material for scanning electron microscopy using 2,2-dimethoxypropane (DMP) and critical-point drying
H HalbritterPMID: 9674883 DOI: 10.3109/10520299809140519
Abstract
A simple, quick, and inexpensive method for preparing any type of pollen material is described. Fresh, mature pollen grains without previous chemical fixation are dehydrated in acidified 2, 2-dimethoxypropane (DMP) followed by critical-point drying in CO2. This method helps preserve size, shape and surface details of both fragile pollen grains and pollen grains that are heavily covered with pollenkitt. Handling of already opened anthers and avoiding loss of pollen grains during the preparation steps are also described. With the DMP direct method, many morphologically and functionally important details that may be lost by conventional methods are well preserved without shrinkage, distortion, or dissolution. The DMP direct method is performed with pollen grains and the results are compared with two other frequently used methods, acetolysis and critical-point drying of chemically fixed material.Triazoxins: Novel nucleosides with anti-Giardia activity
Praveen K Pogula, Atasi De Chatterjee, Miguel Chi, Harrison W VanKoten, Siddhartha Das, Steven E PattersonPMID: 32327222 DOI: 10.1016/j.bmcl.2020.127175
Abstract
Novel nucleoside analogues named "triazoxins" were synthesized. Of these, two analogues were found to be highly effective against Giardia lamblia, an intestinal parasite and a major cause of waterborne infection, worldwide. While compound 7 reduced the growth of trophozoites in culture (IC, ~5 μM), compound 21 blocked the in vitro cyst production (IC
~5 μM). Compound 21 was also effective against trophozoites (IC
, ~36 μM). A third analogue (compound 8) was effective against both trophozoites (IC
, ~36 μM) and cysts (IC
, ~20 μM) although at higher concentration. Thus triazoxin analogues are unique and exhibit morphology (i.e., trohozoites or cysts) -specific effects against Giardia.
Chemical dehydration for rapid paraffin embedding
W Möller, G MöllerPMID: 7819424 DOI: 10.3109/10520299409106304
Abstract
We describe chemical dehydration with 2,2-dimethoxypropane (DMP) for rapid paraffin embedding using a mixture of DMP and mineral oil followed by mineral oil as clearing intermediates. This method is useful for classical histological techniques as well as for histochemistry and immunocytochemistry.Explore Compound Types
