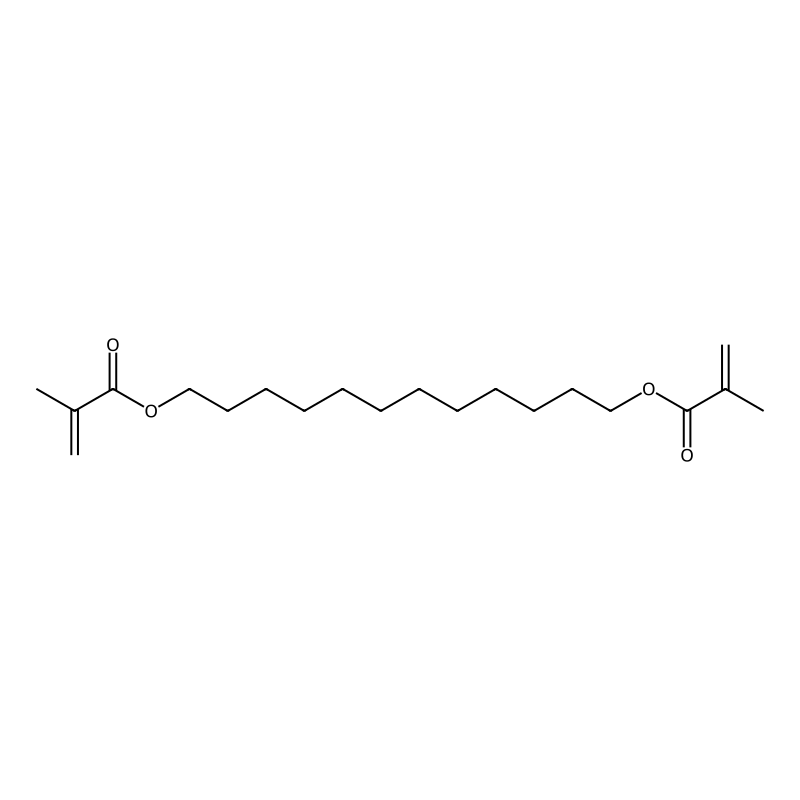
1,12-Dodecanediol dimethacrylate

1,12-Dodecanediol dimethacrylate (DDDMA, CAS 72829-09-5) is a long-chain, hydrophobic, aliphatic dimethacrylate monomer utilized primarily as a reactive diluent and crosslinker in advanced resin formulations, including dental bulk-fill composites, optical coatings, and 3D-printing photopolymers. Characterized by its 12-carbon flexible spacer, DDDMA is procured to modulate the rheology and curing kinetics of rigid base matrices like Bis-GMA and UDMA. Unlike standard short-chain or ether-based diluents, DDDMA uniquely balances the need for low pre-cure viscosity with exceptional post-cure hydrophobicity, making it a critical precursor for applications requiring strict dimensional stability, hydrolytic resistance, and high biocompatibility [1].

Substituting DDDMA with more common, lower-cost diluent monomers such as Triethylene glycol dimethacrylate (TEGDMA) or 1,6-Hexanediol dimethacrylate (HDDMA) fundamentally compromises the final polymer network. TEGDMA contains hydrophilic ether linkages that drastically increase water sorption and hydrolytic degradation in aqueous environments, leading to premature material failure and discoloration. Furthermore, both TEGDMA and HDDMA possess a higher concentration of reactive double bonds per unit mass compared to DDDMA. This higher double-bond density directly translates to significantly greater volumetric polymerization shrinkage and internal stress, which causes marginal gap formation in composites and warping in 3D-printed parts . Consequently, generic substitution fails when procurement demands low-shrinkage, highly hydrophobic, and dimensionally stable polymer networks.

Polymerization Shrinkage Reduction

DDDMA exhibits significantly lower volumetric polymerization shrinkage compared to standard diluents like TEGDMA and HDDMA. Because volumetric shrinkage is directly proportional to the concentration of reacting double bonds per unit volume, DDDMA's long 12-carbon aliphatic chain reduces the overall double-bond density of the formulation. Resin matrices utilizing DDDMA consistently demonstrate lower shrinkage stress and volumetric contraction compared to TEGDMA-based analogs, preventing marginal microleakage and structural warping during the curing process [1].

Procuring DDDMA is essential for manufacturing dimensionally accurate 3D-printed parts and zero-shrinkage structural adhesives.

Water Sorption and Hydrolytic Stability

The hydrophobicity of the diluent monomer dictates the long-term hydrolytic stability of the cured resin. TEGDMA, a common comparator, contains hydrophilic ether oxygen atoms that facilitate water uptake, leading to swelling and degradation. In contrast, DDDMA utilizes a highly hydrophobic 12-carbon aliphatic backbone. Studies evaluating experimental sealants and composites demonstrate that replacing TEGDMA with hydrophobic monomers like DDDMA significantly reduces water sorption and water solubility, extending the lifespan of the polymer in humid or aqueous environments [1].

Buyers formulating marine coatings, dental restoratives, or implantable devices must select DDDMA to prevent water-induced plasticization and degradation.

Enhanced Degree of Conversion

Base monomers like Bis-GMA and UDMA are highly viscous and rigid, causing the polymerizing network to vitrify early and trap unreacted monomers. Adding DDDMA as a reactive diluent increases the free volume and molecular mobility of the system. The long, flexible spacer of DDDMA delays the onset of auto-deceleration and vitrification during curing, allowing the formulation to achieve a significantly higher final degree of conversion (DC) compared to using rigid monomers alone, thereby reducing the leaching of toxic residual monomers [1].

Higher conversion rates improve mechanical strength and are critical for meeting biocompatibility and safety standards by minimizing unreacted monomer leaching.

Low-Shrinkage Bulk-Fill Dental Composites

Driven by its ability to lower volumetric shrinkage and increase the degree of conversion, DDDMA is a premier choice for formulating bulk-fill dental restorative materials. It allows manufacturers to create resins that can be cured in thicker increments (4 mm or more) without generating excessive shrinkage stress that would otherwise cause marginal gap formation [1].

Hydrolytically Stable 3D Printing Photopolymers

Because DDDMA drastically reduces water sorption compared to TEGDMA, it is highly suitable for SLA/DLP 3D printing resins intended for functional parts exposed to moisture or humid environments. Its inclusion prevents the swelling, warping, and mechanical degradation typically seen in standard acrylic or methacrylic printed parts [1].

Biocompatible Medical Device Coatings

The high degree of conversion achieved when using DDDMA minimizes the amount of unreacted, leachable residual monomers. This property, combined with its hydrophobicity, makes DDDMA an ideal crosslinker for biocompatible coatings on medical devices, where preventing cytotoxicity and ensuring long-term stability in bodily fluids are strict procurement requirements [1].