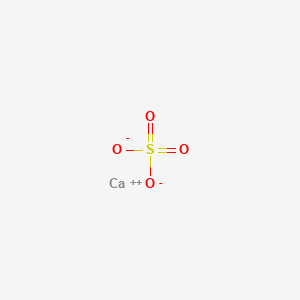
Calcium sulfate

Desiccating Gases and Liquids

• Drying Gases for Analysis: Drierite™ efficiently removes moisture from gases used in experiments. This is crucial for accurate analysis in fields like mass spectrometry and chromatography, where water vapor can interfere with results [].
• Protecting Hygroscopic Materials: Research often involves handling moisture-sensitive materials like enzymes, pharmaceuticals, and certain catalysts. Drierite™ helps maintain a dry environment within containers or desiccators, preventing these materials from absorbing moisture and degrading.

Maintaining a Dry Environment

• Desiccating Storage Containers: Drierite™ can be placed within storage containers for instruments, electronics, or biological samples to control humidity and prevent corrosion, mold growth, or other moisture-related issues [].

Additional Considerations:

• It's important to choose the appropriate type of Drierite™ for the specific application. Some varieties come with an indicator that changes color when saturated, allowing for easy regeneration.
• While generally safe for most research applications, proper handling procedures are recommended as Drierite™ can irritate skin and eyes.

Origin and Significance:

Anhydrous calcium sulfate, the main component of Drierite™, occurs naturally as the mineral gypsum []. However, for use as a desiccant, it is typically produced through a dehydration process involving calcium sulfate dihydrate (CaSO₄•2H₂O). Drierite™ plays a significant role in various scientific research applications by removing moisture from gases and liquids. This dry environment is crucial for many experiments to prevent unwanted reactions with water vapor, ensure accurate measurements, and maintain the stability of sensitive materials.

Molecular Structure Analysis

Key Features:

Calcium sulfate adopts a monoclinic crystal structure. The central Ca²+ cation is coordinated by four sulfate (SO₄²⁻) anions in a tetrahedral arrangement. Each sulfate anion consists of a central sulfur atom surrounded by four oxygen atoms. The strong ionic bonding between these components contributes to the stability of the molecule.

Notable Aspects:

The presence of loosely bound water molecules in the crystal structure of calcium sulfate dihydrate allows for its dehydration to form the anhydrous form (Drierite™). This dehydration process is reversible, and Drierite™ can be regenerated for repeated use by heating it to drive off the absorbed water vapor.

Chemical Reactions Analysis

Synthesis:

Drierite™ is not synthesized in the traditional sense, but rather produced through the dehydration of calcium sulfate dihydrate (gypsum):

CaSO₄•2H₂O (s) → CaSO₄ (s) + 2H₂O (g) ΔH > 0 (endothermic)

Decomposition:

At very high temperatures (> 1450°C), calcium sulfate decomposes to calcium oxide and sulfur trioxide:

CaSO₄ (s) → CaO (s) + SO₃ (g) ΔH > 0 (endothermic)

Other Relevant Reactions:

Drierite™ reacts with water vapor to form calcium sulfate dihydrate:

CaSO₄ (s) + H₂O (g) → CaSO₄•H₂O (s) ΔH < 0 (exothermic)

This reaction is the basis of Drierite™'s desiccating ability. As it absorbs moisture, the color indicator (often cobalt chloride) changes, signifying exhaustion.

Physical And Chemical Properties Analysis

• Melting Point: 1450°C
• Boiling Point: Decomposes before boiling
• Solubility: Slightly soluble in water (around 2 g/L at 20°C)
• Density: 2.9-3.0 g/cm³ []
• Stability: Stable under normal conditions. Insoluble in most organic solvents [].
• Color: White (intrinsic); Indicating versions change color (e.g., blue to pink) upon moisture absorption [].