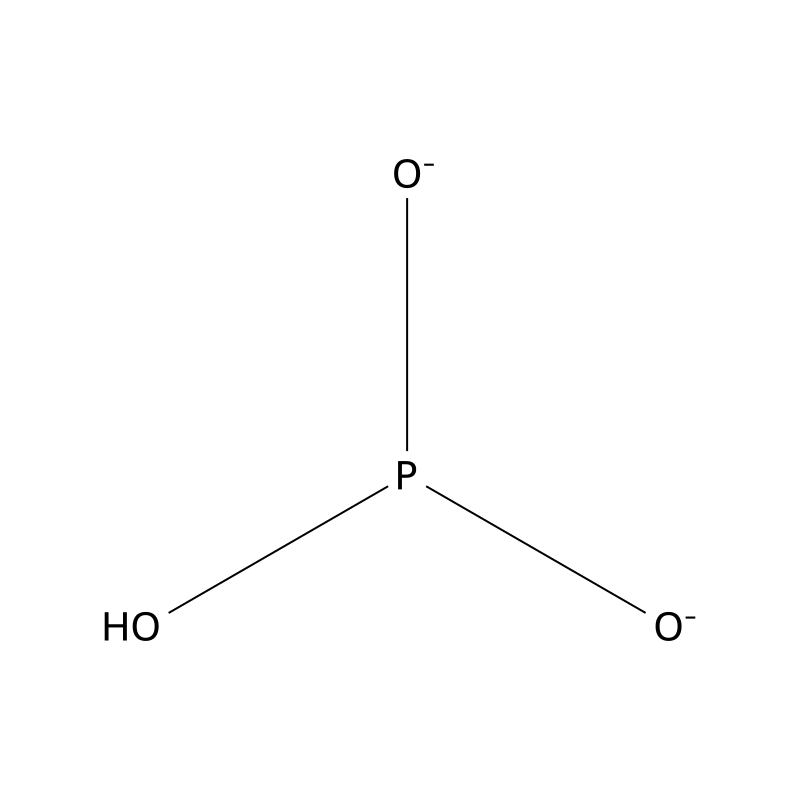
Hydrogenphosphite

Author: Smolecule Technical Support Team. Date: February 2026

A significant point of confusion arises because the IUPAC recommends the names "phosphonate" for the HPO3^2- ion and "hydrogenphosphonate" for the H2PO3- ion, rather than "phosphite" [1]. However, the name "phosphite" remains in common use. The commonly encountered salt, disodium hydrogen phosphite (Na2HPO3), is a white, crystalline solid with reducing properties [4].

Analytical Methodology for Phosphorus-Containing Ions

While a direct protocol for analyzing hydrogen phosphite is not available, a robust High-Performance Liquid Chromatography (HPLC) method for the simultaneous analysis of sodium (Na+) and phosphate (PO4^3-) ions in a complex pharmaceutical suspension provides a relevant and advanced analytical approach [5]. This method is particularly useful for quality control and research settings.

Experimental Protocol: HPLC-ELSD for Simultaneous Sodium and Phosphate Analysis

The following detailed methodology is adapted from a 2025 study [5]:

• Analytical Technique: High-Performance Liquid Chromatography coupled with an Evaporative Light Scattering Detector (HPLC-ELSD).
• Instrumentation & Conditions:
  • Column: Amaze TH mixed-mode column (250 × 4.6 mm, 5 μm), which combines reversed-phase, cation-exchange, and anion-exchange mechanisms.
  • Mobile Phase: 20 mM Ammonium Formate (pH adjusted to 3.2 with formic acid) / Acetonitrile in a 70:30 (v/v) ratio.
  • Flow Rate: 1.0 mL/min.
  • Column Temperature: 40 °C.
  • Injection Volume: 20 μL.
  • ELSD Conditions: Drift tube temperature: 70 °C; Nebulizing gas (N₂) pressure: 3.2 bar.
• Sample Preparation:
  • A volume of 0.5 mL of the sample suspension is diluted with water to a total volume of 5 mL.
  • The solution is shaken vigorously and then centrifuged at 20,000 rcf (relative centrifugal force) for 15 minutes.
  • The supernatant is filtered through a 0.45 μm PTFE syringe filter before injection into the HPLC system [5].

The logical workflow for this analytical protocol is summarized in the following diagram:

HPLC-ELSD Workflow for Ion Analysis

This method is considered a powerful alternative to more complex techniques like ion chromatography or ICP-MS, offering a balance of sensitivity, robustness, and ease of implementation on standard HPLC equipment [5].

Key Scientific Context and Diagrams

The relationship between hydrogen phosphite ions and their parent acid can be clearly visualized. These ions are the conjugate bases of phosphorous acid, and their interconversion depends on the pH of the environment.

Acid-Base Relationships of Phosphorous Acid and Phosphite Ions

References

• 1. Phosphite (ion) [en.wikipedia.org]
• 2. Hydrogen phosphite | HO3P [chemspider.com]
• 3. Chemical Entity Data Page [chemthes.com]
• 4. Disodium hydrogen phosphite [en.wikipedia.org]
• 5. Efficient HPLC-ELSD analysis of sodium and phosphate in ... [pubs.rsc.org]

Author: Smolecule Technical Support Team. Date: February 2026

The hydrogenphosphite anion (H₂PO₃⁻) often acts as a key component in crystal structures, forming extensive hydrogen-bonded networks that provide structural cohesion.

The table below summarizes quantitative crystal data and strong hydrogen-bond interactions from a crystallographic study of cytosinium dihydrogen phosphite [1].

| Unit Cell Dimensions | a = 4.5625 Å, b = 6.4739 Å, c = 6.5933 Å α = 92.934°, β = 91.236°, γ = 98.627° | | Unit Cell Volume | 192.21 ų | | Strong H-Bonds (D-H···A) | N1-H1···O2, O1-H1A···O3, N3-H3···O3, N8-H7···O2 H-bond lengths range from 1.75 Å to 1.94 Å. |

In this structure, the inorganic moieties form a network of H₂PO₃⁻ tetrahedra connected by strong O-H···O hydrogen bonds, creating a two-dimensional network. The organic cations are then bonded to these inorganic layers via N-H···O interactions [1].

Anion Binding Affinity with Synthetic Receptors

Research on bis-urea anion receptors reveals how synthetic molecules can selectively recognize H₂PO₄⁻ (dihydrogen phosphate), which is structurally analogous to H₂PO₃⁻. The thermodynamic parameters offer insights into the binding behavior.

The table below summarizes binding data from isothermal titration calorimetry (ITC) for receptors interacting with TBA-H₂PO₄ (tetrabutylammonium dihydrogen phosphate) in DMF [2].

A key finding is that binding to H₂PO₄⁻ is often entropy-driven, indicated by the favorable negative TΔS° term. This is likely due to the release of solvent molecules (water) upon the anion binding to the receptor [2].

Emerging Applications & Protocols

Electrocatalysis for Seawater Splitting

A 2025 study reports an ammonium iron hydrogen phosphite (FeHPhi) electrocatalyst. The [HPO₃]²⁻ oxoanion acts as a Lewis base, creating a chloride-repellant ("chlorophobic") environment that protects the anode from corrosion in seawater. This property is crucial for developing durable catalysts for hydrogen production via seawater electrolysis [3].

Experimental Protocol: Single-Crystal Growth for X-ray Diffraction

The following workflow visualizes the crystallization method used to prepare the cytosinium dihydrogen phosphite single crystal for structural analysis [1]:

Crystal Growth Workflow [1]

Experimental Protocol: Anion Binding Studies

For determining binding affinity, researchers used Isothermal Titration Calorimetry (ITC) and ¹H NMR Titration [2]:

• ITC: A solution of the bis-urea receptor (2 mM in DMF) was titrated with a tetrabutylammonium anion salt (TBA-H₂PO₄, 50 mM in DMF) at 25°C. The heat change for each injection was measured to calculate binding constant (K_b), enthalpy (ΔH°), and stoichiometry (n).
• ¹H NMR Titration: A solution of the receptor was titrated with the anion salt. Chemical shift changes of the urea N-H protons were monitored to determine binding constants and understand interaction geometry.

References

• 1. Hydrogen bonding in cytosinium dihydrogen phosphite - PMC [pmc.ncbi.nlm.nih.gov]
• 2. influence of receptor structure and anion nature on binding ... [pubs.rsc.org]
• 3. Chlorophobic Iron Hydrogen Phosphite as OER-Active ... [pubmed.ncbi.nlm.nih.gov]

Author: Smolecule Technical Support Team. Date: February 2026

Fundamental Chemistry & Relationship

Phosphorous acid (H₃PO₃) is a diprotic oxyacid of phosphorus, despite having three hydrogen atoms. Its structure and acid-base behavior are key to understanding its relationship with hydrogenphosphite.

• Molecular Structure and Tautomerism: The predominant structure of phosphorous acid in the solid state and aqueous solution is the phosphonic acid tautomer, HP(O)(OH)₂ [1]. This molecule features a direct P-H bond and two P-OH bonds [1]. It exists in equilibrium with a minor trihydroxy tautomer, P(OH)₃, but the equilibrium constant is vastly in favor of the HP(O)(OH)₂ form (K = 10¹⁰·³ at 25°C) [1].
• Acid-Base Properties and Nomenclature: Phosphorous acid dissociates in two steps, yielding the this compound ion [1]. The following table details the dissociation sequence and official nomenclature.

It is critical to note that the hydrogen atom directly bonded to phosphorus is not readily ionizable in aqueous conditions. Therefore, H₃PO₃ is diprotic, not triprotic [1]. The IUPAC recommended name for the HPO₃²⁻ ion is phosphonate, but This compound remains common in chemical literature [1].

Physicochemical Properties

The table below summarizes key properties of phosphorous acid for experimental design.

Preparation & Synthesis

A common laboratory and industrial method for preparing phosphorous acid is the controlled hydrolysis of phosphorus trichloride (PCl₃) [1] [2].

• Standard Hydrolysis Protocol: The reaction is highly exothermic [2]. Procedure: Under efficient stirring and with ice-water cooling, add phosphorus trichloride slowly to distilled water, controlling the drop rate to prevent a violent reaction [2]. After the addition is complete, the mixture is heated below 140°C and evaporated to about one-third of its original volume to drive off hydrogen chloride (HCl) gas [2]. The resulting solution is cooled to 60-85°C, seeded with a small amount of phosphorous acid crystals, and then further cooled with stirring to crystallize the pure product [2].
• Alternative Solvent Method: To better control the reaction, PCl₃ can be dissolved in an inert solvent like carbon tetrachloride (CCl₄) before the slow addition of water [2]. After the reaction, the acid solution is separated, washed with CCl₄, and the HCl is removed under reduced pressure over a water bath (not exceeding 60°C) before cooling and crystallization [2].
• Industrial Synthesis: On an industrial scale, PCl₃ is often sprayed into steam at 190°C, with the heat of reaction used to distill off HCl and excess water [1] [3].

Analytical Methodologies

Accurate determination of phosphorus species is crucial in chemical and environmental research. The following table outlines common and advanced techniques.

Research & Application Protocols

Phosphorous acid and its salts are valuable in organic synthesis and other applied research areas.

• Synthesis of α-Aminophosphonic Acids: Phosphorous acid can be used in a one-pot, three-component reaction with an amine and an aldehyde or ketone to synthesize α-aminophosphonic acids, which are biologically active analogues of amino acids [5]. Typical Protocol: A mixture of the carbonyl compound (e.g., acetone), amine (e.g., benzylamine or a secondary amine like pyrrolidine), and phosphorous acid is heated at an elevated temperature (e.g., 100°C) to yield the α-aminophosphonic acid derivative [5].
• Acid Catalysis: Phosphorous acid serves as a mild, less corrosive, and commercially available Brønsted acid catalyst [5]. It has been successfully used for highly regioselective hydroarylation reactions of phenols with alkenes, producing alkylated products in high yields (85–93%) with excellent selectivity [5].
• Redox Chemistry: Phosphorous acid is a strong reducing agent. A characteristic test is the reduction of mercuric chloride (HgCl₂) first to white mercurous chloride (Hg₂Cl₂) and then to black mercury metal (Hg) on heating or standing [1]. This property also means it slowly oxidizes in air to phosphoric acid [1]. Upon heating to about 200°C, it undergoes a disproportionation reaction to phosphoric acid and phosphine (PH₃), a toxic and flammable gas [1] [3].

The redox behavior is central to many of its applications, from water treatment agents to PVC stabilizers [1] [3]. The experimental workflow for its synthesis and primary applications can be visualized as follows:

References

• 1. Phosphorous acid [en.wikipedia.org]
• 2. Preparation and Application Phosphorous acid [chemicalbook.com]
• 3. Phosphorous Acid Structure – H 3 PO 3 [byjus.com]
• 4. A Review of Recent Developments in Analytical Methods ... [mdpi.com]
• 5. Phosphorous Acid - an overview [sciencedirect.com]

Author: Smolecule Technical Support Team. Date: February 2026

The term "hydrogenphosphite" is not specifically detailed in the search results. However, the data on phosphine (PH₃), a highly toxic and flammable gas, is highly relevant because many phosphorus-containing inorganic salts can decompose or react to produce phosphine gas [1] [2].

The table below summarizes the critical hazard information for phosphine from official U.S. occupational safety sources (OSHA and NIOSH) [1] [2].

| Major Hazards | • Toxicity: Highly toxic by inhalation. • Flammability: Flammable gas, can ignite spontaneously in air [2]. • Chemical Incompatibility: Reacts with air, oxidizers, chlorine, acids, and moisture [2]. | | OSHA PEL (8-hour TWA) | 0.3 ppm (0.4 mg/m³) [1] [2] | | NIOSH REL (10-hour TWA) | 0.3 ppm (0.4 mg/m³) [2] | | NIOSH REL (STEL) | 1 ppm (1 mg/m³) [2] | | NIOSH IDLH | 50 ppm [2] | | Target Organs | Respiratory system [2] |

Key Safety Principles for Phosphorus Compounds

Based on the identified hazards of phosphine gas, which may be generated from this compound compounds, the following safety principles are critical.

• Decomposition Risk: Be aware that this compound salts may decompose, especially in the presence of acids, moisture, or heat, to release phosphine gas [2]. All procedures should be planned to minimize these conditions.
• Engineering Controls: Work within a certified fume hood or under local exhaust ventilation to ensure toxic gas does not enter the laboratory atmosphere.
• Exposure Monitoring: Use continuous gas monitoring systems if the potential for phosphine release exists. Personal air monitoring may also be necessary.
• Personal Protective Equipment (PPE): At a minimum, wear appropriate lab coat, gloves, and safety goggles. Based on the potential exposure risk, consult the NIOSH respirator recommendations for phosphine to determine if a respirator is required [2].
• Emergency Preparedness: Have a written emergency plan that includes procedures for responding to accidental releases and exposures. Know the symptoms of exposure, which can include nausea, difficulty breathing, and muscle pain [2].

The logical relationships between the hazards of phosphine and the necessary safety controls can be visualized in the following workflow:

This diagram outlines the core safety logic: identifying phosphine gas as the key hazard when handling this compound compounds and linking it to essential laboratory safety controls.

References

• 1. PHOSPHINE | Occupational Safety and Health Administration [osha.gov]
• 2. NIOSH Pocket Guide to Chemical Hazards - Phosphine [cdc.gov]

Author: Smolecule Technical Support Team. Date: February 2026

The table below summarizes key physicochemical properties of phosphite (HPO₃²⁻) and related compounds, synthesized from the available literature.

Experimental Protocols: Phosphite Transformation

Recent prebiotic chemistry studies detail methods to observe phosphite transformations, which illustrate its stability under controlled conditions [1].

Objective

To demonstrate the oxidation and condensation of phosphite into pyrophosphite and orthophosphate under mild thermal conditions simulating a prebiotic environment.

Materials

• P Source: Sodium phosphite dibasic pentahydrate (Na₂HPO₃·5H₂O)
• Additives: Urea, and optionally, prebiotic minerals/salts (e.g., CaSO₄·2H₂O, MgCl₂, NaCl, kaolinite clay)
• Equipment: Glass vials (20 mL), hot plate, magnetic stirrer, pH paper

Methodology

This procedure is adapted from a 2023 study on prebiotic chemistry [1].

• Preparation: Dissolve 0.100–0.150 g of sodium phosphite in 7 mL of deionized water in a glass vial. Add 0.5 g of urea and any other additives to test their influence.
• Initial Measurement: Check the initial pH of the solution (expected to be around 8.0–8.5).
• Thermal Cycling (Wet-Dry Cycles):
  • Heat the uncapped vial on a hot plate at 78–83°C for 24 hours until the mixture is dry.
  • Rehydrate the sample with 7 mL of deionized water.
  • Repeat this heating and rehydration cycle. The total experimental time is typically 72 hours, culminating in complete dryness.
• Analysis: The solid reaction products can be analyzed using techniques like ³¹P NMR spectroscopy to identify and quantify the formation of new phosphorus species, such as orthophosphate, pyrophosphite, and isohypophosphate.

Transformation Pathways of Phosphite

The following diagram illustrates the key transformation pathways of phosphite under experimental prebiotic conditions, showing its role as a central precursor to more complex molecules.

This pathway shows phosphite as a hub molecule capable of forming condensed P compounds, oxidizing to phosphate, or reacting with organic molecules [1].

Gaps and Research Considerations

• Limited Data on Specific Salts: While data exists for sodium and aluminum hydrogen phosphite, a comprehensive dataset for the entire family of hydrogen phosphite salts is not available in the search results.
• Biological Signaling Pathways: The search results do not provide direct evidence that hydrogen phosphite itself acts on specific human signaling pathways (e.g., MAPK, Akt). Its biological role is discussed primarily in the context of hydrogen sulfide (H₂S) in thermal waters, which is a distinct molecule [3].
• Toxicology Data: Dimethyl hydrogen phosphite has associated toxicological data from animal studies [2], but similar comprehensive safety profiles for inorganic hydrogen phosphites are not detailed here.

References

• 1. Prebiotic Chemistry of Phosphite: Mild Thermal Routes to ... [pmc.ncbi.nlm.nih.gov]
• 2. Dimethyl Hydrogen Phosphite - NCBI - NIH [ncbi.nlm.nih.gov]
• 3. Frontiers | Biological Effects of Thermal Water-Associated Hydrogen... [frontiersin.org]

Author: Smolecule Technical Support Team. Date: February 2026

Hydrogen phosphites, particularly those of transition metals, are an important class of materials in modern chemical research, showing significant promise in energy-related applications like electrocatalysis for hydrogen production [1] [2]. These protocols detail the synthesis of selected aluminium, nickel-iron, and cobalt-based hydrogen phosphite materials, which are notable for their role in creating efficient and energy-saving catalytic systems [3] [1].

Protocol 1: Synthesis of Aluminium Hydrogen Phosphite

This protocol describes the preparation of aluminium hydrogen phosphite, a compound identified for its utility as a flame retardant in polymers [3].

• Primary Application: Used as a flame retardant additive in various polymers, including thermosetting plastics (e.g., epoxy resins, polyester), and thermosoftening plastics (e.g., polyurethane) [3].

• Detailed Synthesis Procedure:

  • Reaction: Add phosphorous acid and water to a reaction vessel. Introduce a water-soluble aluminium salt (e.g., aluminium sulfate, aluminium hydroxide) to the mixture. The molar ratio of phosphorous acid to the aluminium salt should be controlled.
  • Heating and Stirring: Heat the reaction mixture to a temperature between 50°C and 90°C with continuous stirring for a duration of 1 to 5 hours.
  • Crystallization: After the reaction, cool the mixture to room temperature to allow for the crystallization of the product.
  • Isolation and Washing: Collect the solid product via filtration or centrifugation. Wash the precipitate with a suitable solvent, followed by drying to obtain the final aluminium hydrogen phosphite [3].

• Formulation as a Flame Retardant: The synthesized aluminium hydrogen phosphite can be mixed with the target polymer. For instance, a composition might include 100 parts by weight of polymer and 1 to 100 parts by weight of aluminium hydrogen phosphite. Other common flame retardant synergists, such as ammonium polyphosphate or zinc oxide, may be incorporated as required [3].

Protocol 2: Electrodeposition of Amorphous Nickel-Iron Hydrogen Phosphite (NixFe1-x(H2PO2)2) Electrocatalysts

This advanced protocol outlines a one-step electrodeposition method to create amorphous bimetallic hydrogen phosphite catalysts on a conductive substrate for electrochemical hydrogen production [1].

• Primary Application: Serves as a high-performance, non-noble metal-based electrocatalyst for the hydrogen evolution reaction (HER) and urea oxidation reaction (UOR), enabling energy-saving hydrogen production coupled with wastewater purification [1].

• Detailed Synthesis Procedure:

  • Solution Preparation: Prepare an aqueous electrodeposition solution containing nickel ions (Ni²⁺), iron ions (Fe³⁺), and hypophosphite ions (H₂PO₂⁻). The concentration of metal ions can be adjusted to tailor the final composition (NixFe1-x(H2PO2)2).
  • Electrochemical Setup: Use a standard three-electrode cell system.
    • Working Electrode: Nickel foam (NF) substrate.
    • Counter Electrode: A platinum sheet or graphite rod.
    • Reference Electrode: Saturated calomel electrode (SCE) or Ag/AgCl.
  • Electrodeposition: Immerse the electrodes in the solution and perform electrodeposition via a constant potential (potentiostatic) or constant current (galvanostatic) method. During this process, Ni²⁺, Fe³⁺, and H₂PO₂⁻ ions are co-deposited onto the nickel foam, forming an amorphous layer [1].

The workflow for this synthesis is as follows:

Performance Data of Synthesized Hydrogen Phosphites

The tables below summarize key performance metrics for the hydrogen phosphite materials described in the protocols.

Table 1: Electrocatalytic Performance of NixFe1-x(H2PO2)2

| Material Composition | Application | Performance Metric | Value | | :--- | :--- | :--- | :--- | | Ni₀.₇Fe₀.₃(H₂PO₂)₂ | Hydrogen Evolution Reaction (HER) | Overpotential @ 10 mA cm⁻² | 92 mV [1] | | Ni(H₂PO₂)₂ | Urea Oxidation Reaction (UOR) | Potential @ 10 mA cm⁻² | 1.31 V [1] | | Ni₀.₇Fe₀.₃(H₂PO₂)₂ || Ni(H₂PO₂)₂ | Coupled HER||UOR System | Cell Voltage @ 10 mA cm⁻² | 1.43 V [1] |

Table 2: Overview of Other Hydrogen Phosphite Compounds and Synthesis Methods

Conclusion and Research Outlook

Hydrogen phosphite compounds, particularly those of transition metals, are accessible through wet-chemical and electrochemical methods. The synthesized materials, especially those with amorphous and bimetallic structures, demonstrate exceptional performance in electrocatalysis, rivaling noble-metal catalysts in some cases [1] [2]. This makes them highly attractive for sustainable energy technologies. Future research directions may focus on optimizing these synthesis protocols further, exploring the hydrogen phosphite chemistry of other metals, and scaling up production for industrial application.

Reference List

• Google Patents. Hydrogen phosphite aluminium, Its Preparation Method And Use. CN104093663B. Provides the detailed synthesis protocol and flame retardant application of aluminium hydrogen phosphite [3].
• Zhang, K. et al. Adjustable composition of nickel–iron hydrogen phosphite for urea-assisted energy-saving hydrogen production. 2025. Describes the electrodeposition, performance, and theoretical analysis of NixFe1-x(H2PO2)2 electrocatalysts [1].
• Structural Chemistry. (C2N2H10)[Co(HPHO3)2Cl2]: the first phosphite analog of layered hydrogen selenites. 2024. Details the crystal structure and synthesis of a novel cobalt hydrogen phosphite compound [4].
• ChemRxiv. Efficient Hydrogen Production on Crystalline-Amorphous Heterostructured Cobalt Boride-Phosphite Electrocatalyst. 2025. Preprint on the high-performance cobalt-based catalyst synthesis [2].
• Google Patents. Production of dialkyl hydrogen phosphites. US2862948A. Historical patent on the synthesis of organic hydrogen phosphites [5].

References

• 1. Adjustable composition of nickel–iron hydrogen phosphite ... [sciencedirect.com]
• 2. Efficient Hydrogen Production on Crystalline-Amorphous ... [chemrxiv.org]
• 3. Hydrogen phosphite aluminium, Its Preparation Method ... [patents.google.com]
• 4. (C2N2H10)[Co(HPHO3) 2Cl2]: the first phosphite analog of layered... [link.springer.com]
• 5. US2862948A - Production of dialkyl hydrogen phosphites [patents.google.com]

Author: Smolecule Technical Support Team. Date: February 2026

1. Introduction Dialkyl hydrogen phosphites (general formula (RO)₂P(O)H) are important organophosphorus compounds characterized by a phosphorus-hydrogen (P-H) bond. Their chemical behavior is influenced by a tautomeric equilibrium between the phosphonite form (P(III), (RO)₂P(O)H) and the phosphonate form (P(V), (RO)₂P(O)H), making them valuable building blocks in organic synthesis and effective additives in industrial applications [1].

2. Key Applications

• Versatile Synthetic Intermediates: They serve as reactants for constructing carbon-phosphorus (C–P) bonds, enabling synthesis of β-ketophosphonates, α-aminophosphonic acids, and other functionalized phosphorus compounds [1].
• Promoters for Heteroaromatic Functionalization: They activate heteroaromatic N-oxides, such as quinoline N-oxides, facilitating direct amination, alkylation, and other C–H functionalization reactions to produce valuable nitrogen-containing heterocycles [1].
• Extreme Pressure/Anti-Wear Additives: They are used in lubricants to protect metal surfaces like gears and vanes from wear and scuffing, with performance varying based on molecular structure [2].

3. Quantitative Performance Data The table below summarizes performance data for various dialkyl hydrogen phosphites as extreme pressure/anti-wear additives, demonstrating the critical influence of alkyl chain structure.

Table 1: Performance of Dialkyl Hydrogen Phosphites as Lubricant Additives [2]

Table 2: Dielectric Thermal Analysis (DETA) Data of Phosphites [2]

4. Structure-Activity Relationships

• Alkyl Chain Length: Shorter alkyl chains (e.g., butyl) confer higher reactivity and superior performance as anti-wear additives compared to longer chains (e.g., lauryl) [2].
• Polarity and Surfactancy: Phosphites with shorter chains exhibit higher dielectric conductivity and surfactancy, promoting more uniform and deeper reaction with metal surfaces to form protective layers [2].
• Thermodynamic Stability: The P-H bond in these compounds can be cleaved under electrochemical conditions, enabling their use in novel, greener synthetic pathways for organophosphorus molecules [3].

Experimental Protocols

Protocol 1: Synthesis of Dialkyl Hydrogen Phosphites via Ammonia Neutralization

This classic method produces dialkyl hydrogen phosphites from phosphorus trichloride and alcohols [4].

Workflow Diagram: Phosphite Synthesis via Ammonia Neutralization

Materials:

• Phosphorus trichloride (PCl₃)
• Desired alcohol (ROH; e.g., methanol, ethanol, butanol)
• Anhydrous ammonia gas (NH₃)
• Inert, low-boiling solvent (e.g., n-hexane, diethyl ether)
• Equipment: Three-necked flask, dropping funnel, thermometer, gas inlet tube, mechanical stirrer, ice bath, filtration setup, distillation apparatus.

Procedure:

• Charge and Cool: Place 2.0 equivalents of the anhydrous alcohol and the solvent into the reaction flask. Cool the mixture to 0-5°C using an ice bath.
• Slow Addition: Add 1.0 equivalent of PCl₃ dropwise via the dropping funnel with vigorous stirring. Maintain the temperature below 30°C to suppress side reactions.
• Ammonia Introduction: After PCl₃ addition, begin bubbling anhydrous ammonia gas into the reaction mixture. Continue external cooling to keep the temperature below 30-35°C. The reaction produces a white precipitate of ammonium chloride (NH₄Cl).
• Completion: Continue adding ammonia until the mixture is basic to moist litmus paper.
• Filtration: Filter the reaction mixture to remove the solid NH₄Cl salt. Wash the filter cake with a small amount of cold solvent.
• Solvent Removal: Combine the filtrate and washes, and remove the volatile solvent under reduced pressure using a rotary evaporator.
• Product Distillation: Purify the crude product by vacuum distillation. Collect the fraction boiling at the characteristic temperature and pressure for the target dialkyl hydrogen phosphite.

Notes:

• Strict temperature control during PCl₃ and NH₃ addition is critical for high yield and purity.
• All equipment must be thoroughly dried to prevent hydrolysis.
• The stoichiometry of PCl₃ : ROH : NH₃ is typically 1 : 2 : >2 [4].

Protocol 2: Oxidative Esterification of Monoalkyl Phosphonates

This method converts monoalkyl hydrogen phosphonates to dialkyl phosphates, demonstrating a key transformation of phosphorus compounds [5].

Materials:

• Monoalkyl hydrogen phosphonate (RO-P(O)(H)OH)
• Alcohol (R'OH)
• Bromine (Br₂) in pyridine, OR Carbon tetrachloride (CCl₄) and triethylamine (Et₃N)
• Anhydrous pyridine (if using bromine)
• Equipment: Round-bottom flask, stirrer, nitrogen inlet, syringe, ice bath.

Procedure:

• Using Bromine/Pyridine:
  • Dissolve the monoalkyl phosphonate and 1.0 equivalent of the alcohol (R'OH) in anhydrous pyridine under a nitrogen atmosphere.
  • Cool the solution to 0°C.
  • Add 1.0 equivalent of bromine dropwise via syringe with stirring.
  • Allow the reaction to warm to room temperature and stir until completion (monitor by TLC or ³¹P NMR).
  • Work up by carefully quenching and extracting the product.
• Using CCl₄/Triethylamine:
  • Dissolve the monoalkyl phosphonate and 1.0 equivalent of the alcohol (R'OH) in an inert solvent like dichloromethane.
  • Add 1.0 equivalent of triethylamine.
  • Add 1.0 equivalent of carbon tetrachloride.
  • Stir the reaction mixture at room temperature until complete.
  • Work up by washing with water and concentrating the organic layer.

Notes:

• The bromine/pyridine method can also be used without an added alcohol to produce sym-dialkyl dihydrogen pyrophosphates in good yield [5].
• These are oxidative conditions; the phosphorus atom is oxidized from the +3 to the +5 oxidation state.

References

• 1. Applications of H-phosphonates for C element bond ... [degruyterbrill.com]
• 2. properties of dialkyl hydrogen phosphites and iron [sciencedirect.com]
• 3. Recent advances in the electrochemical synthesis of ... [beilstein-journals.org]
• 4. US2864847A - Production of dialkyl hydrogen phosphites [patents.google.com]
• 5. Studies in phosphorylation. Part XXIX. The synthesis of dialkyl ... [pubs.rsc.org]

Author: Smolecule Technical Support Team. Date: February 2026

As a Precursor to Organophosphorus Compounds

A primary application of hydrogenphosphite salts is serving as a phosphorus source for synthesizing valuable organophosphorus compounds, which are crucial in agrochemicals, pharmaceuticals, and materials science.

Synthesis of H-Phosphonate Diesters

Protocol: Nickel-Catalyzed Synthesis of H-Phosphonate Diesters from Sodium Hypophosphite [1]

• Objective: To directly convert sodium hypophosphite into H-phosphonate diesters, which are key platform molecules in organophosphorus chemistry.

• Reaction Principle: A nickel-catalyzed cross-coupling that bridges homogeneous and heterogeneous catalysis.

• Materials:

  • Sodium hypophosphite monohydrate (NaH₂PO₂·H₂O)
  • Aryl iodide electrophile
  • Nickel catalyst (e.g., Ni@CPOL-dppp & PPh₃, a supported catalyst system)
  • Solvent (e.g., Toluene or DMF)
  • Base (e.g., K₂CO₃ or Cs₂CO₃)

• Procedure:

  • Add sodium hypophosphite (1.0 equiv), the aryl iodide (2.2 equiv), the nickel catalyst (e.g., 2-5 mol%), and a base (2.5 equiv) to a dried reaction vessel.
  • Purge the system with an inert gas (N₂ or Ar).
  • Add the degassed solvent via syringe.
  • Heat the reaction mixture to 100-120 °C and monitor by TLC or LC-MS.
  • Upon completion, cool the mixture to room temperature.
  • Dilute with ethyl acetate and wash with water and brine.
  • Purify the crude product via column chromatography on silica gel.

• Key Data for Aryl H-Phosphonate Synthesis [1]

Hydrophosphorylation of Alkynes

Protocol: Palladium-Catalyzed Asymmetric Hydrophosphorylation of Alkynes [1]

• Objective: To synthesize P-stereogenic phosphinates from alkynes and sodium hypophosphite with high enantiocontrol.
• Reaction Principle: A palladium-catalyzed reaction that adds a P-H bond across a carbon-carbon triple bond.
• Materials:
  • Sodium hypophosphite monohydrate (NaH₂PO₂·H₂O)
  • Alkyne substrate
  • Palladium catalyst (e.g., Pd₂(dba)₃·CHCl₃)
  • Chiral ligand (e.g., (R)-SEGPHOS or (S)-BINAP)
  • Solvent (e.g., 1,4-Dioxane)
• Procedure:
  • In a glove box, combine the palladium catalyst (2.5 mol%), chiral ligand (3.0 mol%), and solvent in a Schlenk tube.
  • Stir the mixture at room temperature for 30 minutes to pre-form the catalytic complex.
  • Add the alkyne substrate (0.2 mmol) and sodium hypophosphite (1.5 equiv).
  • Seal the tube, remove it from the glove box, and heat at 100 °C for 24-48 hours.
  • After cooling, dilute the reaction mixture with dichloromethane.
  • Filter through a short pad of Celite and concentrate under reduced pressure.
  • Purify the residue by preparative TLC or column chromatography to obtain the enantiomerically enriched phosphinate.

As a Reducing Agent

Hypophosphites function as mild hydride donors in various reductive transformations, often replacing more hazardous reagents.

Hydrodehalogenation

Protocol: Palladium-Catalyzed Hydro-dehalogenation of Aryl Halides [1]

• Objective: To replace aryl halides with hydrogen, a key step in deprotection or detoxification.

• Reaction Principle: A catalytic cycle where hypophosphite serves as a hydrogen source.

• Materials:

  • Sodium hypophosphite (NaH₂PO₂)
  • Aryl halide substrate (Cl, Br, I)
  • Palladium catalyst (e.g., Pd/C or Pd-gC₃N₄)
  • Solvent (e.g., Isopropanol)
  • Base (e.g., NaOAc)

• Procedure:

  • Charge a reaction vial with the aryl halide (1.0 equiv), Pd-gC₃N₄ catalyst (10 mg), NaOAc (2.0 equiv), and NaH₂PO₂ (2.0 equiv).
  • Add isopropanol as solvent.
  • Heat the mixture at 80 °C for 2-4 hours.
  • Monitor reaction progress by GC-MS or TLC.
  • Upon completion, filter the reaction mixture through a pad of Celite to remove the catalyst.
  • Concentrate the filtrate and purify the product via flash chromatography or recrystallization.

• Key Data for Hydrodehalogenation [1]

Reductive Amination

Protocol: Catalyst-Free Reductive Amination Using Sodium Hypophosphite [1]

• Objective: To convert aldehydes or ketones into primary, secondary, or tertiary amines.
• Reaction Principle: A one-pot, two-step process involving imine formation followed by hypophosphite-mediated reduction.
• Materials:
  • Sodium hypophosphite monohydrate (NaH₂PO₂·H₂O)
  • Aldehyde or ketone substrate
  • Amine substrate
  • Solvent (e.g., Methanol or Ethanol)
• Procedure:
  • To a solution of the carbonyl compound (1.0 equiv) and the amine (1.2 equiv for primary amines; 2.4 equiv for ammonia to target primary amines) in methanol, add molecular sieves (4Å).
  • Stir the mixture at room temperature for 2-12 hours to form the imine intermediate.
  • Add sodium hypophosphite (1.5 equiv) to the reaction mixture.
  • Heat the resulting suspension at 60 °C for 6-12 hours.
  • After cooling, filter the mixture to remove molecular sieves and any solids.
  • Concentrate the filtrate under reduced pressure.
  • Take up the residue in ethyl acetate, wash with a saturated NaHCO₃ solution, dry over Na₂SO₄, filter, and concentrate.
  • Purify the crude amine product via distillation or column chromatography.

In Catalytic C-C Bond Forming Reactions

Organic hydrogen phosphites can act as effective catalysts for key carbon-carbon bond-forming reactions.

Protocol: Friedel-Crafts Amidoalkylation of Indoles [2]

• Objective: To catalyze the synthesis of 3-indolyl methanamine derivatives, important structural motifs in pharmaceuticals.

• Reaction Principle: Organic hydrogen phosphites act as mild Brønsted acid catalysts.

• Materials:

  • Dimethyl hydrogen phosphite (or similar organic hydrogen phosphite)
  • Indole
  • N-Ts-aryl aldimine
  • Solvent (Toluene)

• Procedure:

  • In a dried vial, dissolve the N-Ts-aryl aldimine (1.0 equiv) and indole (1.05 equiv) in dry toluene.
  • Add dimethyl hydrogen phosphite (20 mol%) as a catalyst.
  • Stir the reaction mixture at room temperature for the time specified (e.g., 2 hours for the model substrate).
  • Monitor the reaction by TLC.
  • Upon completion, quench the reaction with a saturated aqueous NaHCO₃ solution.
  • Extract the product with ethyl acetate (3 x 15 mL).
  • Combine the organic layers, dry over Na₂SO₄, filter, and concentrate.
  • Purify the crude product by recrystallization or column chromatography to obtain the 3-indolyl methanamine derivative.

• Key Data for Friedel-Crafts Catalysis [2]

  • Catalyst: Dimethyl hydrogen phosphite (1a)
  • Loading: 20 mol%
  • Solvent: Toluene
  • Temperature: Room Temperature
  • Yield: ~50% for model substrate (with formation of some bisindole byproduct). The yield can be optimized by varying the hydrogen phosphite structure and reaction conditions.

The following diagram summarizes the core applications and workflows of hydrogenphosphites in organic synthesis.

Safety and Handling Notes

• General Toxicity: Sodium hypophosphite is recognized as having low acute toxicity (rat oral LD₅₀ > 1440 mg/kg) and is considered a non-hazardous substance for both people and the environment, making it a preferable choice [1].
• Ester Derivatives: In contrast, ester derivatives like dimethyl hydrogen phosphite require more careful handling. It is classified as suspected of causing genetic defects and cancer (H341, H351) [3]. It is a colorless liquid with a boiling point of 170–171 °C and should be used only in a well-ventilated hood.
• Byproduct Management: Certain reduction reactions may produce phosphine (PH₃) gas, which is highly toxic and has a pungent odor [4]. These reactions must be conducted in an efficient fume hood, and evolving gases should be scrubbed by bubbling through a trap containing bleach (sodium hypochlorite solution) [4].
• Moisture Sensitivity: Sodium hypophosphite monohydrate readily absorbs moisture from the air and should be stored in a cool, dry place [1].

Conclusion and Future Perspectives

Hydrogenphosphites, particularly sodium hypophosphite, have solidified their role as versatile, efficient, and sustainable reagents in the synthetic chemist's toolbox. Their primary applications as precursors to organophosphorus compounds and as mild reducing agents are well-established in protocols for hydrodehalogenation, reductive amination, and cross-coupling reactions [1]. Furthermore, their utility as Brønsted acid catalysts in C-C bond-forming reactions highlights their functional diversity [2].

Future developments are likely to focus on:

• Expanding Asymmetric Catalysis: Designing new chiral frameworks around hydrogenphosphites for enantioselective synthesis.
• Photoredox and Electrochemical Applications: Exploring the synergy between hypophosphites and modern activation modes.
• Bioconjugation and Medicinal Chemistry: Leveraging their mild and selective reducing nature for modifying biomolecules.
• Flow Chemistry: Developing continuous processes for large-scale, safe utilization of this compound chemistry.

Given their safety profile, cost-effectiveness, and reactivity, hydrogenphosphites are poised for continued growth in application, aligning with the principles of green and sustainable chemistry.

References

• 1. Mini-update on the applications of Hypophosphites in ... [sciencedirect.com]
• 2. Organic hydrogen phosphites and hydrogen phosphates ... [sciencedirect.com]
• 3. Dimethyl hydrogen phosphite - NCBI - NIH [ncbi.nlm.nih.gov]
• 4. (R)-(−)-1,1'-binaphthyl-2,2'-diyl hydrogen phosphate [orgsyn.org]

Author: Smolecule Technical Support Team. Date: February 2026

Detailed Experimental Protocols

Protocol 1: Enzymatic Fluorometric Assay in Microtiter Plate Format

This protocol is adapted from the method described by López et al. (2011) for quantifying phosphite in biological and environmental samples [1].

1. Principle The assay utilizes the enzyme phosphite dehydrogenase (PTXD), which catalyzes the oxidation of phosphite to phosphate, using NAD+ as a co-substrate. The reaction produces NADH, which in turn reduces resazurin to the highly fluorescent product, resorufin, in a reaction catalyzed by diaphorase. The fluorescence intensity is proportional to the phosphite concentration [1].

2. Equipment & Reagents

• Equipment: Fluorometer capable of reading 96-well microtiter plates, multi-channel pipettes, incubator.
• Reagents:
  • Recombinant phosphite dehydrogenase (PTXD)
  • NAD+
  • Resazurin
  • Diaphorase
  • Assay buffer (e.g., Tris-HCl or HEPES, pH 8.0)
  • Standard solutions of phosphite (e.g., 0-100 µM)

3. Procedure

• Sample Preparation: Extract and clarify your samples (e.g., plant tissue homogenate, water sample). For plant tissues, a suitable extraction buffer is needed [1].
• Reaction Setup: In each well of a black 96-well plate, add:
  • 50 µL of sample or phosphite standard.
  • 50 µL of master mix containing:
    • Assay buffer
    • 1 mM NAD+
    • 0.01% resazurin
    • 0.1 U/mL diaphorase
    • Recombinant PTXD enzyme
• Incubation: Incubate the plate at 30°C for 30-60 minutes, protected from light.
• Fluorescence Measurement: Read the fluorescence using a fluorometer with excitation at 560 nm and emission at 590 nm.
• Data Analysis: Generate a standard curve from the phosphite standards and calculate the phosphite concentration in unknown samples.

The workflow for this protocol is outlined below.

Protocol 2: Affinity Measurement Using Bacterial Binding Proteins and MST

This protocol is based on the work of McSorley et al. (2017) to study the ultra-high affinity binding of phosphite to bacterial periplasmic binding proteins (PBPs) like Te_PtxB [2].

1. Principle Microscale Thermophoresis (MST) measures the motion of molecules along a microscopic temperature gradient. Binding of a ligand (phosphite) to a fluorescently labeled protein (PBP) changes the protein's hydration shell, size, and charge, altering its thermophoretic behavior. This change is used to calculate the binding affinity (Dissociation constant, Kd) [2].

2. Equipment & Reagents

• Equipment: Microscale Thermophoresis instrument, capillary tubes.
• Reagents:
  • Purified recombinant Periplasmic Binding Protein (e.g., Te_PtxB, Pm_PhnD, Ps_PtxB) with a His-tag.
  • RED-tris-NTA fluorescent dye (for His-tag labeling).
  • Ligand solutions: Phosphite, phosphate, methylphosphonate, etc.

3. Procedure

• Protein Labeling:
  • Purify the recombinant PBP (e.g., Te_PtxB).
  • Label the protein by incubating it with the RED-tris-NTA dye at a recommended ratio (e.g., 100 nM protein with dye from the commercial kit) for 30 minutes in the dark [2].
• Ligand Dilution Series: Prepare a serial dilution of the phosphite ligand (e.g., from 10 mM down to 0.3 nM) in assay buffer.
• Sample Preparation: Mix a constant concentration of the labeled protein (e.g., 50 nM) with each concentration of the ligand dilution series. Use a constant volume (e.g., 10 µL).
• Loading & Measurement:
  • Load each sample into a dedicated MST capillary.
  • Place the capillaries in the MST instrument.
  • Measure the thermophoresis at room temperature using appropriate instrument settings (e.g., 20-40% LED power, medium MST power).
• Data Analysis: The instrument software analyzes the normalized fluorescence (Fnorm) vs. ligand concentration to determine the dissociation constant (Kd).

The workflow for studying the molecular basis of phosphite binding is as follows.

Key Insights for Method Selection

• For High Sensitivity and Throughput: The Enzymatic Fluorometric Assay is ideal for processing many samples (e.g., environmental monitoring) with high sensitivity [1].
• For Studying Specificity and Mechanism: MST with Bacterial PBPs provides deep insights into the molecular interactions and astonishingly high affinity (nanomolar Kd) that microbes have evolved for phosphite scavenging [2].
• For Volatile Phosphite Esters: GC-based methods (GC-FID, GC-MS) are required for detecting and quantifying alkyl phosphite derivatives like dimethyl hydrogen phosphite in environmental and industrial samples [3].

I hope these detailed application notes and protocols assist in your research. Should you need to delve deeper into the structural aspects or require information on other derivatives, please do not hesitate to ask.

References

• 1. An enzymatic fluorescent assay for the quantification of ... [pubmed.ncbi.nlm.nih.gov]
• 2. The molecular basis of phosphite and hypophosphite ... [pmc.ncbi.nlm.nih.gov]
• 3. Dimethyl hydrogen phosphite - NCBI - NIH [ncbi.nlm.nih.gov]

Author: Smolecule Technical Support Team. Date: February 2026

Introduction to PCl₃-Methanol Reaction Chemistry

The reaction of phosphorus trichloride (PCl₃) with methanol represents a fundamental transformation in organophosphorus chemistry with significant implications across pharmaceutical, agricultural, and industrial applications. This reaction enables the efficient synthesis of phosphite esters and hydrogenphosphites, which serve as versatile intermediates in the production of organophosphorus compounds. The strategic importance of these compounds stems from their diverse applications as pesticide precursors, pharmaceutical intermediates, flame retardants, and ligands for catalysis [1] [2]. Understanding the controlled pathways of this reaction is essential for researchers and development professionals seeking to exploit phosphorus chemistry in targeted synthetic applications.

The PCl₃-methanol reaction system demonstrates remarkable synthetic versatility, with product profiles highly dependent on reaction stoichiometry, temperature control, presence of base, and solvent environment [3] [4] [5]. This technical overview provides detailed experimental protocols, safety considerations, and analytical methodologies to enable researchers to reliably target specific phosphite products while minimizing hazardous byproducts. The fundamental chemistry proceeds through a sequential substitution mechanism where methoxy groups progressively replace chloride atoms on phosphorus, with the final product determined by whether the reaction is conducted in the presence or absence of a base [2].

Reaction Fundamentals and Competing Pathways

Chemical Principles and Mechanisms

The reaction between phosphorus trichloride and methanol proceeds through a nucleophilic substitution mechanism where the oxygen atom of methanol attacks the electrophilic phosphorus center in PCl₃. This process initiates a complex reaction network with competing pathways that can be directed toward different products through careful control of experimental conditions. The phosphorus atom in PCl₃ exhibits pnictogen bonding capability, acting as a Lewis acid through its σ-hole region opposite to the P-Cl bonds, while the lone pair on phosphorus can also facilitate Lewis base behavior [6] [2]. This dual reactivity underpins the complex behavior of PCl₃ in nucleophilic environments.

Gas-phase studies using matrix isolation infrared spectroscopy have revealed that the initial interaction between PCl₃ and methanol involves the formation of a noncovalent adduct stabilized primarily through P···O pnictogen bonding rather than conventional hydrogen bonding [4] [6]. This adduct represents the crucial first intermediate in the substitution pathway. Computational analyses at B3LYP/6-311++G(d,p) and MP2/6-311++G(d,p) levels indicate that the P-bonded adduct is more stable than the H-bonded alternative by approximately 1.56 kcal/mol, highlighting the driving force for the observed reaction trajectory [6]. The subsequent reaction steps involve sequential displacements of chloride ions by methoxy groups, with the liberation of hydrogen chloride as a byproduct.

Competing Reaction Pathways

The product distribution in the PCl₃-methanol system is governed by three competing pathways that can be manipulated through stoichiometric control and reaction conditions:

• Phosphite Ester Formation (With Base): When the reaction is conducted in the presence of a tertiary amine base such as diethylaniline or triethylamine, the hydrogen chloride byproduct is efficiently scavenged, preventing further reactions and leading to the formation of trimethyl phosphite as the primary product [7] [2]. This pathway follows a straightforward substitution mechanism where all three chloride atoms are replaced by methoxy groups: PCl₃ + 3CH₃OH + 3R₃N → P(OCH₃)₃ + 3R₃NH⁺Cl⁻ [2].

• Dialkyl Hydrogenphosphite Formation (Without Base): In the absence of a base and with excess methanol, the reaction takes a different trajectory, resulting in the formation of dimethyl this compound ((CH₃O)₂P(O)H) along with hydrochloric acid and methyl chloride as byproducts [3] [8] [2]. This transformation involves an Arbuzov-type rearrangement where one alkyl group is eliminated as alkyl chloride. The stoichiometry for this pathway is: PCl₃ + 3CH₃OH → (CH₃O)₂P(O)H + 2HCl + CH₃Cl [2].

• Monosubstituted Intermediate Formation: With strict stoichiometric control (1:1 molar ratio) and in the absence of base, the reaction can be halted at the monosubstituted stage, producing methoxyphosphorodichloridite (CH₃OPCl₂) [2]. This intermediate is highly reactive and can be further functionalized to access diverse phosphorus-containing compounds.

Table 1: Product Distribution Based on Reaction Conditions

The following diagram illustrates the competing reaction pathways and their dependence on base presence:

Experimental Protocols

Laboratory-Scale Synthesis of Trimethyl Phosphite

This protocol describes the synthesis of trimethyl phosphite using a modified McCombie-Saunders-Stacey approach with diethylaniline as the acid scavenger, producing high-purity product in approximately 83% yield [7].

Materials and Equipment:

• Phosphorus trichloride (PCl₃), freshly distilled, 137.5 g (87.5 mL, 1 mole)
• Absolute methanol, anhydrous, 96 g (121 mL, 3 moles)
• Diethylaniline, freshly distilled, 447 g (477 mL, 3 moles)
• Petroleum ether (b.p. 40-60°C), dry, 1.4 L total
• 3-L three-necked round-bottom flask
• Sealed mechanical stirrer
• Efficient reflux condenser
• 500-mL dropping funnel
• Sintered-glass funnel
• Vigreux column (75 cm)
• Cold-water bath

Procedure:

• Prepare a solution of absolute methanol (3 moles) and diethylaniline (3 moles) in 1 L of dry petroleum ether in the 3-L flask.
• Equip the flask with the stirrer, reflux condenser, and dropping funnel. Place the assembly in a cold-water bath.
• Dissolve phosphorus trichloride (1 mole) in 400 mL of dry petroleum ether in the dropping funnel.
• With vigorous stirring, add the PCl₃ solution dropwise at a rate that maintains gentle boiling toward the end of the addition (approximately 30 minutes total).
• After complete addition, heat the mixture under gentle reflux with continuous stirring for 1 hour. A copious precipitate of diethylaniline hydrochloride will form.
• Cool the suspension to room temperature and filter under suction through a sintered-glass funnel.
• Compress the amine salt cake firmly and wash with five 100-mL portions of dry petroleum ether.
• Combine the filtrate and washings, then concentrate by distillation at water-bath temperature through the Vigreux column.
• Transfer the residue to a pear-shaped flask and distill under reduced pressure (16 mm Hg) using the Vigreux column.
• Collect the product fraction boiling at 57-58°C/16 mm Hg as colorless trimethyl phosphite.
• Characterize the product by refractive index (n₍D,25⁰C⁾: 1.4104-1.4106) and density (d₍4,20⁰C⁾: 0.963).

Notes and Troubleshooting:

• Critical: Use thoroughly anhydrous methanol to prevent hydrolysis and reduced yields.
• Efficient stirring is essential to prevent local accumulation of HCl, which can lead to ethyl chloride formation and contamination with diethyl hydrogen phosphite.
• The recovered petroleum ether and fore-run can be recycled in subsequent batches to increase yields to 86-90%.
• For scale-up, maintain the same stoichiometric ratios and consider continuous processing for improved safety profile.

Industrial-Scale Synthesis of Dimethyl this compound

This protocol details the industrial preparation of dimethyl this compound via the base-free reaction of PCl₃ with excess methanol, following an Arbuzov rearrangement pathway [3] [8].

Materials and Equipment:

• Phosphorus trichloride (PCl₃), 413 g (3 moles)
• Anhydrous methanol, 320 g (10 moles)
• Butane or hexane as solvent, 665 g total
• Jacketed reactor with temperature control and HCl scrubbing system
• Distillation apparatus for product purification

Procedure:

• Charge the reactor with anhydrous methanol (320 g) dissolved in butane (400 mL).
• Cool the mixture to approximately 0°C using the jacketed cooling system.
• Prepare a solution of PCl₃ (413 g) in butane (265 g).
• Gradually add the PCl₃ solution to the methanol over 2 hours with efficient agitation, maintaining the temperature at 0°C.
• During addition, continuously remove the generated hydrogen chloride using a suitable scrubbing system.
• After complete addition, allow the reaction mixture to warm slowly to room temperature with continued mixing.
• Separate the crude product from the solvent and byproducts through fractional distillation.
• Purify dimethyl this compound through vacuum distillation to achieve high purity (>99%).
• Confirm product identity by NMR spectroscopy and GC-MS analysis.

Process Optimization:

• Temperature control at 0°C during PCl₃ addition is critical to minimize side reactions and ensure high yield (90-93%).
• Efficient HCl removal prevents reverse reactions and decomposition pathways.
• Solvent choice (low-boiling alkanes) facilitates product separation and recycling.
• Continuous processing options can improve efficiency for large-scale production.

Continuous Industrial Manufacturing Process

For large-scale production, continuous processes offer advantages in safety and efficiency. The following protocol is adapted from patent literature [5]:

System Configuration:

• Pre-mixing vessel for methanol/solvent preparation
• Multi-stage reactor with precise temperature zones
• In-line separation for HCl removal
• Fractional distillation columns for product purification
• Solvent recycling system

Procedure:

• Prepare methanol in an inert solvent (cyclohexane, toluene, or methylcyclohexane) at specified concentration.
• Introduce PCl₃ and methanol solution in stoichiometric ratio into the first reaction stage.
• Maintain temperature control through sequential reaction zones (0°C → 25°C → 50°C).
• Remove HCl vapor continuously under reduced pressure with appropriate scrubbing.
• Separate the crude product stream from the solvent and byproducts.
• Purify through fractional distillation under vacuum.
• Recycle solvent to the initial stage for economic efficiency.

Key Process Parameters:

• Molar ratio control critical for product specificity
• Vapor phase processing options for improved purity
• Catalyst systems (e.g., sulfur, selenium) can enhance rearrangement efficiency
• Automated control systems for temperature and stoichiometry

Data Analysis and Characterization

Experimental Parameters and Yield Optimization

Table 2: Optimization Parameters for Phosphite Ester Synthesis

Spectroscopic Characterization Data

Table 3: Spectral Characteristics of Phosphorus-Methanol Reaction Products

Safety and Handling Considerations

Hazard Assessment and Control Measures

The reaction of phosphorus trichloride with methanol involves significant hazards that require rigorous safety protocols:

• Phosphorus Trichloride Hazards: PCl₃ is highly toxic, corrosive, and reacts violently with water and alcohols, releasing hydrogen chloride gas [2]. The NIOSH recommended exposure limit (REL) is 0.2 ppm (TWA) and 0.5 ppm (STEL), with an IDLH of 25 ppm [2]. Personal protective equipment must include chemical-resistant clothing, face shield, and appropriate respiratory protection when engineering controls are insufficient.

• Reaction Exothermicity: The substitution reaction is highly exothermic and requires careful temperature control to prevent thermal runaway. Laboratory-scale reactions should employ cooling baths and controlled addition rates, while industrial processes require jacketed reactors with emergency cooling capacity [7].

• Hydrogen Chloride Management: Gaseous HCl is produced in substantial quantities and must be effectively captured using scrubber systems containing alkaline solutions (e.g., NaOH or Ca(OH)₂). Proper ventilation is essential to prevent corrosion and exposure hazards [5] [7].

Waste Management and Environmental Considerations

• Byproduct Recovery: Diethylaniline hydrochloride from the base-assisted reaction can be filtered, washed, and potentially regenerated to the free base for recycling [7].
• Solvent Recycling: Petroleum ether and other hydrocarbon solvents should be recovered and purified for reuse through distillation systems.
• Neutralization Streams: Aqueous waste from acid scrubbing requires neutralization before disposal, with potential recovery of sodium chloride or calcium chloride salts.

Applications in Research and Industry

Pharmaceutical Applications

Phosphite esters synthesized through the PCl₃-methanol reaction serve as key intermediates in pharmaceutical development. Dimethyl this compound is employed in the synthesis of phosphonate prodrugs and nucleotide analogs with antiviral activity [8]. The Ludwig-Eckstein phosphorylation method, which utilizes phosphite intermediates, is widely applied in the formation of triphosphates for nucleotide synthesis [3]. These compounds are essential for developing antiviral agents such as tenofovir and adefovir, which are used in the treatment of HIV and hepatitis B.

Agricultural and Industrial Applications

• Pesticide Synthesis: Phosphite esters are precursors to organophosphate pesticides and herbicides through subsequent oxidation and derivatization. The herbicide glyphosate is produced via phosphonomethylation using PCl₃ with amines and formaldehyde [2].
• Flame Retardants: Phosphite esters are converted to phosphate esters like triphenyl phosphate and tricresyl phosphate, which function as effective flame retardants and plasticizers for PVC and other polymers [8] [2].
• Ligands and Catalysts: Chiral phosphite ligands derived from this chemistry are used in asymmetric catalysis for pharmaceutical synthesis [3]. These ligands enable highly enantioselective hydrogenation and carbon-carbon bond formation reactions.

The following diagram illustrates the major application pathways for phosphite esters:

Conclusion

The reaction of phosphorus trichloride with methanol represents a versatile and industrially significant transformation for producing valuable phosphite esters and hydrogenphosphites. Through careful control of reaction stoichiometry, temperature, and acid scavenging, researchers can direct the reaction toward specific products with high selectivity and yield. The protocols outlined in this document provide reproducible methodologies for synthesizing both trimethyl phosphite and dimethyl this compound at laboratory and industrial scales, with comprehensive characterization data to verify product identity and purity.

The applications of these phosphite intermediates span pharmaceutical development, agricultural chemistry, and industrial material science, underscoring the continued importance of this fundamental reaction in modern chemical synthesis. Future developments in this area will likely focus on continuous processing for improved safety, catalytic approaches for enhanced sustainability, and novel derivatives with tailored properties for specialized applications. By adhering to the detailed protocols and safety considerations outlined herein, researchers can reliably exploit this chemistry to advance their synthetic objectives in drug development and materials science.

References

• 1. Solvent and solvation effects on reactivities and ... [frontiersin.org]
• 2. Phosphorus trichloride [en.wikipedia.org]
• 3. Phosphorus Trichloride - an overview [sciencedirect.com]
• 4. Gas phase reaction of phosphorus trichloride and methanol [sciencedirect.com]
• 5. US3184495A - Process for the preparation and recovery of ... [patents.google.com]
• 6. a matrix isolation infrared and ab initio computational study [pubmed.ncbi.nlm.nih.gov]
• 7. triethyl phosphite [orgsyn.org]
• 8. Dimethyl Phosphite (DMP, DMPi) [vinuthana.com]

Author: Smolecule Technical Support Team. Date: February 2026

Purification Techniques: Application Notes

The table below summarizes three key purification methods for phosphorus-containing compounds, drawing on recent research.

| Ion Exchange [1] | Swapping impurity ions with counter-ions on a solid resin. | - Resin Type: Strongly basic anion exchanger (e.g., IRA-400).

• Contact Time: Sufficient for equilibrium.
• Scale: Can be scaled for larger volumes. | - ~90% removal of phosphate from a solution.
• Minimal loss of the primary compound's strength. | Removing anionic impurities (e.g., phosphate) from hydrogen peroxide and other oxidizing solutions [1]. | | Solvent Extraction [2] [3] | Separating compounds based on differential solubility in two immiscible liquids. | - Solvent: n-Butanol shows highest efficiency.
• Temperature: 25-60°C (little impact).
• Acid Concentration: Higher P₂O₅ content increases distribution factor. | Distribution Factor (25°C):
• n-Butanol: 0.178 to 0.436
• Tributyl Phosphate: 0.120 to 0.320
• Outcome: Concentrated acid (56-63% P₂O₅) with low impurity (≤0.002% H₂SO₄) [3]. | Purifying wet-process phosphoric acid to a highly concentrated, technical grade [2] [3]. | | Donnan Dialysis (Electromembrane) [4] | Using an ion-exchange membrane and a driving ion (H⁺) to selectively remove cationic impurities. | - Membrane: Perfluorinated sulfonic acid CEM.
• Driving Solution: 5 mol/L Nitric Acid.
• Agitation: Intensive to reduce liquid film resistance. | Cation Removal Flux Order: Mg²⁺ > Al³⁺ > Fe³⁺.
• Efficient removal of metallic cations (Fe³⁺, Al³⁺, Mg²⁺) from phosphoric acid. | Purification of wet-process phosphoric acid, specifically for removing metallic cations that hinder downstream processing [4]. |

Experimental Protocol: Ion Exchange for Phosphate Removal

This protocol is adapted from a study on decontaminating hydrogen peroxide solutions, a method that can be extrapolated for removing anionic impurities from other sensitive matrices [1].

Workflow Overview

The diagram below illustrates the ion exchange purification process.

Materials

• Ion Exchange Resin: Strongly basic anion exchange resin, such as IRA-400 (chloride form) [1].
• Column: A glass or plastic chromatography column with a porous frit.
• Solutions:
  • Regeneration Solution: 1 M Sodium chloride (NaCl) or hydrochloric acid (HCl).
  • Rinsing Solution: Deionized water.
  • Sample Solution: The solution containing the target compound and phosphate impurities.

Step-by-Step Procedure

• Resin Pretreatment: Pre-condition the resin according to the manufacturer's instructions. This typically involves rinsing with several bed volumes of deionized water, followed by the regeneration solution (e.g., 1 M NaCl), and a final rinse with deionized water until the eluent is neutral.
• Column Packing: Slurry the pre-treated resin in deionized water and carefully pour it into the column. Avoid introducing air bubbles. Allow the resin to settle under gravity flow.
• Sample Loading: Pass the sample solution through the resin bed at a controlled flow rate (e.g., 1-2 mL/min). Ensure the sample matrix is compatible with the resin.
• Washing and Collection: After loading, wash the resin bed with 2-3 bed volumes of deionized water. Combine the washings with the initial eluent. This combined fraction is your purified product.
• Resin Regeneration: Regenerate the resin for reuse by passing several bed volumes of the regeneration solution (1 M NaCl), followed by thorough rinsing with deionized water until the effluent is neutral.

Summary and Recommendations

The purification strategy must be tailored to the specific nature of your "hydrogen phosphite" compound and its key impurities.

• For removing anionic impurities like phosphate from a sensitive solution, ion exchange with a resin like IRA-400 is a robust and scalable method [1].
• For purifying a crude phosphoric acid stream on a larger scale, solvent extraction with n-butanol is highly effective for deep purification and concentration [3].
• For the selective removal of cationic metallic impurities (e.g., Fe³⁺, Al³⁺) from an acidic phosphorus stream, Donnan Dialysis offers an efficient membrane-based alternative [4].

References

• 1. Phosphate removal from hydrogen peroxide solutions ... [pubmed.ncbi.nlm.nih.gov]
• 2. A Case of Wet-process Phosphoric Acid Based On Karatau ... [sciencedirect.com]
• 3. A Case of Wet-process Phosphoric Acid Based On Karatau ... [openchemicalengineeringjournal.com]
• 4. Purification of Wet-Process Phosphoric Acid via Donnan ... [pmc.ncbi.nlm.nih.gov]

Author: Smolecule Technical Support Team. Date: February 2026

Understanding Hydrogenphosphites

In industrial and chemical contexts, "hydrogenphosphite" typically refers to dialkyl hydrogen phosphites (e.g., diethyl hydrogen phosphite), which are esters of phosphorous acid with the general structure (RO)₂P(=O)H [1]. These compounds are different from phosphite salts (e.g., sodium hydrogen phosphite) and are primarily used as key intermediates in the synthesis of other organophosphorus compounds, such as phosphonates (via the Michaelis-Arbuzov reaction), which have applications as pharmaceuticals, agrochemicals, and flame retardants [1] [2].

Historical Production Method from Patent Literature

A primary method for producing dialkyl hydrogen phosphites involves the esterification of phosphorus trichloride (PCl₃) with an alcohol, followed by hydrolysis. The following table summarizes the key steps and conditions from a 1953 patent [3].

The workflow below illustrates the general sequence of this production process.

Figure 1: General workflow for the production of dialkyl hydrogen phosphites via esterification and hydrolysis.

Laboratory-Scale Synthesis Protocol

The following is a detailed methodology for the synthesis of diisopropyl methylphosphonate, which is prepared from diisopropyl hydrogen phosphite via an Arbusov rearrangement. This illustrates how a hydrogen phosphite is used in a subsequent reaction to form a final product [2].

• Objective: To synthesize diisopropyl methylphosphonate from triisopropyl phosphite and methyl iodide.
• Principle: The Arbusov rearrangement, where a trialkyl phosphite reacts with an alkyl halide to form a dialkyl alkylphosphonate.
• Hazard Warning: This procedure involves handling reactive and toxic chemicals, including methyl iodide and phosphorus compounds. It must be conducted by trained personnel in a fume hood with appropriate personal protective equipment (PPE) [2] [4].

Materials and Equipment

• Reactants:
  • Triisopropyl phosphite (416 g, 453 ml, 2 mol). Note: Must be free of diisopropyl hydrogen phosphite contaminant.
  • Methyl iodide (284 g, 113 ml, 2 mol)
• Equipment:
  • 2-liter round-bottomed flask
  • Water-cooled condenser
  • Dropping funnel
  • Heating mantle (or gauze with free flame)
  • Vigreux column (50-75 cm)
  • Distillation apparatus with vacuum pump
  • Dry Ice trap

Procedure

• Setup: Assemble the 2-liter flask with the condenser and dropping funnel. Add the methyl iodide and a few pieces of porous plate to the flask.
• Initiation: Add about 50 ml of triisopropyl phosphite to the flask. Heat the mixture until an exothermic reaction begins, then immediately remove the heat source.
• Addition: Slowly add the remainder of the triisopropyl phosphite via the dropping funnel at a rate that maintains a brisk boil. Reapply heat if necessary towards the end of the addition.
• Reflux: After the addition is complete, fit the condenser for reflux and boil the mixture gently for 1 hour.
• Solvent Recovery: Replace the condenser with the Vigreux column and distillation apparatus. Distill off the bulk of the isopropyl iodide byproduct at atmospheric pressure (85-95°C).
• Product Distillation: Transfer the residue to a pear-shaped flask and distill under reduced pressure using a vacuum pump (interpose a Dry Ice trap).
  • First, recover the remaining isopropyl iodide at water-pump pressure.
  • Then, fractionate the product at a higher vacuum. Diisopropyl methylphosphonate distills at 51°C / 1.0 mmHg.
• Analysis: The yield is 308-325 g (85-90%). The product is a colorless liquid with a refractive index ( n_D^{20} ) of 1.4101 [2].

Critical Safety Considerations

Working with phosphorus compounds requires extreme caution.

• Phosphorus Trichloride (PCl₃): This is a highly corrosive and reactive liquid that reacts violently with water, releasing heat and hydrogen chloride (HCl) gas [3].
• Phosphorus Allotropes: White (or yellow) phosphorus is extremely toxic and flammable, causing severe burns and systemic poisoning. It must be stored under water and handled with great care. Red phosphorus is more stable but may contain white phosphorus as a contaminant [5] [4].
• Phosphine Gas (PH₃): Both white and red phosphorus can generate highly toxic phosphine gas upon contact with strong bases or under certain conditions [5] [4].
• Personal Protective Equipment (PPE): At a minimum, wear safety glasses, impervious gloves, and a fire-retardant lab coat. Operations generating dust or using large quantities should be conducted in an inert atmosphere, such as a glove box [5].

References

• 1. Organophosphorus chemistry - Wikipedia [en.m.wikipedia.org]
• 2. diisopropyl methylphosphonate [orgsyn.org]
• 3. US2862948A - Production of dialkyl hydrogen phosphites [patents.google.com]
• 4. White Phosphorus: Systemic Agent | NIOSH [cdc.gov]
• 5. Phosphorus | Office of Environmental Health and Safety [ehs.princeton.edu]

Author: Smolecule Technical Support Team. Date: February 2026

The table below summarizes major impurity types and effective removal strategies based on current research.

Detailed Experimental Protocols

Here are detailed methodologies for two key impurity removal processes.

Protocol 1: Acid Leaching and Lime Solidification for Phosphorus & Fluorine

This method is highly effective for converting and solidifying stubborn phosphorus and fluorine impurities [3].

• Step 1: Acidification

  • Materials: Raw phosphogypsum (or similar material), Concentrated sulfuric acid.
  • Procedure: Directly add a small quantity of sulfuric acid to the solid gypsum material. Heat the mixture to a suitable temperature (e.g., 120°C) for a defined period. This step dissolves eutectic phosphorus and converts fluorine impurities into volatile H₂SiF₆ and HF, which are removed from the system [3].
  • Safety Note: This step must be performed in a well-ventilated fume hood due to the evolution of toxic and corrosive HF gas.

• Step 2: Lime Solidification

  • Materials: Acid-treated solid, Lime (CaO or Ca(OH)₂).
  • Procedure: Add lime to the acid-treated solid. The lime neutralizes the material and reacts with phosphorus and fluorine impurities to form highly insoluble Ca₅(PO₄)₃F (fluorapatite), effectively stabilizing the contaminants [3].
  • Validation: The treatment is successful if the leaching solution meets environmental standards for phosphorus and fluorine (e.g., ρ(P) < 0.4 mg/L, ρ(F⁻) < 1.5 mg/L) [3].

Protocol 2: Deep Phosphorus Removal via Crystal Modification & Phase Transformation

This advanced technique uses a dissolution-recrystallization process to remove lattice-bound (co-crystalline) phosphorus and can be adapted for high-value product synthesis [2].

• Principle: The process involves dissolving the crude gypsum (CaSO₄·2H₂O) and recrystallizing it into alpha-calcium sulfate hemihydrate (α-HH). This phase transformation releases phosphorus trapped in the crystal lattice into the solution, where it can be washed away [2].

• Workflow: The following diagram illustrates the key stages of this recrystallization-based purification method.

• Detailed Procedure [2]:

  • Create Reaction Medium: Prepare a mixed solution of NaCl and HCl. The NaCl promotes the formation of the desired α-HH crystal form, while the HCl creates an acidic condition that keeps the released phosphorus in a soluble state.
  • Atmospheric Heating: Add the impure solid to the reaction medium and heat the mixture to 90-100°C under atmospheric pressure with stirring for several hours.
  • Filtration and Washing: After the phase transformation is complete, filter the resulting crystals and wash them thoroughly with hot water or a dilute acidic solution to remove any surface-adsorbed phosphorus.

Key Synthesis & Troubleshooting Insights

• Synthesis By-Product Control: During the synthesis of phosphites like Irgafos 168 from PCl₃, steric hindrance can lead to by-products like phosphorochloridites and HCl. Using catalysts (e.g., amines like DMF) and appropriate solvents (e.g., xylene, toluene) can significantly improve yield and purity. A mild vacuum treatment or aqueous wash with a base like NaOH can help remove these halogenated by-products [4].
• Adapting these Methods: The protocols above are described in the context of purifying phosphogypsum (PG). However, the chemistry of phosphorus and fluorine impurity removal—particularly through acid leaching, lime solidification, and dissolution-recrystallization—is widely applicable. You can adapt these principles to your specific hydrogenphosphite synthesis by adjusting parameters like acid concentration, temperature, and solid-to-liquid ratio.

References

• 1. Review of the State of Impurity Occurrences and ... [mdpi.com]
• 2. Deep removal of phosphorus and synchronous preparation ... [sciencedirect.com]
• 3. Research on the technology and mechanism of direct ... [sciencedirect.com]
• 4. Recent Advances in the Synthesis of Commercially ... [pmc.ncbi.nlm.nih.gov]

Author: Smolecule Technical Support Team. Date: February 2026

The table below summarizes key information on phosphorus compounds from the search results, which provides context for understanding decomposition pathways.

Experimental Protocols and Methodologies

Here are detailed methodologies based on the stabilization strategies identified in the search results.

Protocol 1: Stabilized Generation of Phosphine Gas

This protocol uses a formulation to safely generate phosphine without auto-ignition, adapted from patent literature [4].

• Objective: To generate phosphine gas in a controlled manner, preventing violent reaction and auto-ignition.
• Materials:
  • Technical aluminium phosphide (85% AlP) powder.
  • Zinc stearate.
  • Ammonium carbamate.
  • Urea.
  • Tablet press or equipment for forming pellets/granules.
  • Gas-tight generation vessel with a metering device for water addition.
• Procedure:
  • Formulation Preparation: Prepare a homogeneous mixture of 70% technical aluminium phosphide, 20% ammonium carbamate, 9.8% urea, and 0.2% zinc stearate by weight [4].
  • Tableting: Press the mixture into tablets or pellets of the required weight (e.g., 0.6 g) [4].
  • Controlled Hydrolysis: Place the tablets in a generation vessel. Use a metering device to introduce liquid water gradually over a prolonged period (e.g., add 50 g of tablets to 50 ml of water over several hours) [4].
  • Monitoring: Monitor the reaction temperature. The stabilized formulation should not exceed 37°C, whereas an unstabilized mixture can reach over 90°C and ignite [4].

Protocol 2: Handling and Storage of Hypophosphorous Acid (50% Solution)

This protocol outlines practices to prevent the decomposition of hypophosphorous acid, based on its documented chemical properties [1].

• Objective: To store and handle hypophosphorous acid without triggering decomposition into phosphorous acid and phosphine.
• Materials:
  • Hypophosphorous acid, 50% aqueous solution.
  • Cool, dark storage facility.
  • Inert atmosphere (e.g., nitrogen or argon) if necessary.
• Procedure:
  • Storage: Maintain the acid as a 50% aqueous solution in its original, tightly sealed container [1].
  • Temperature Control: Store at low temperatures and avoid heating. Do not heat solutions above 90°C to avoid reaction with water, and never above 110°C to prevent disproportionation [1].
  • Anhydrous Acid Preparation (Advanced): For experiments requiring anhydrous acid, use continuous extraction with diethyl ether. Note: Anhydrous acid is highly susceptible to oxidation and disproportionation [1].

Conceptual Workflow for Decomposition Prevention

The diagram below illustrates a generalized experimental workflow for preventing the decomposition of sensitive phosphorus compounds, integrating principles from the search results.

Key Stabilization Principles for Your Research

To guide your work with hydrogen phosphite, here are the core chemical principles derived from the search results:

• Control Reaction Kinetics: The use of zinc compounds (e.g., zinc stearate, zinc oxide) alongside ammonium ions (e.g., from ammonium carbamate) was found to dramatically slow down the hydrolysis of aluminium phosphide and lower the reaction temperature, preventing ignition [4]. This principle of using chemical stabilizers to modulate reaction speed is widely applicable.
• Use Inert Diluents: Incorporating substances that release carbon dioxide and ammonia upon contact with moisture helps dilute the phosphine gas as it is generated, moving its concentration below the explosive limit [2] [3]. This is a key safety measure for handling gases prone to combustion.
• Manage Environmental Factors: Decomposition is often accelerated by heat and moisture [2] [1] [4]. Strict temperature control and the use of desiccants or moisture barriers in storage are fundamental to maintaining compound stability.

References

• 1. Hypophosphorous acid [en.wikipedia.org]
• 2. Chemicals used as fumigants (cont.) - Phosphine [fao.org]
• 3. Phosphine (PH) [phytosanitarysolutions.com]
• 4. Hydrogen-phosphide releasing compositions and their use [patents.google.com]

Author: Smolecule Technical Support Team. Date: February 2026

The troubleshooting guides and data below are based on a foundational study of the anation reaction of [Co(NH₃)₅H₂O]³⁺ by H₃PO₃/H₂PO₃⁻ [1]. This reaction produces [CoH₂PO3(NH₃)₅]²⁺ and was studied in a temperature range of 60 to 80 °C and an acidity range of [H⁺] = 1.5 × 10⁻¹ M to 2.0 × 10⁻³ M [1].

Key findings from this study indicate:

• Only H₂PO₃⁻ was found to be reactive, not H₃PO₃ [1].
• The rate data was consistent with an I_d mechanism (dissociative interchange) [1].
• The mean value for outer-sphere association between [Co(NH₃)₅H₂O]³⁺ and H₂PO₃⁻ was determined to be 1.5 M⁻¹ [1].

Frequently Asked Questions & Troubleshooting

Experimental Protocol Summary

Based on the kinetic study, the general methodology involved [1]:

• Preparation of Reactants: The pentaamineaquacobalt(III) complex, [Co(NH₃)₅H₂O]³⁺, is used as the starting material.
• Setting Reaction Conditions: Reactions are run in solutions with carefully controlled acidity ([H⁺]) and a constant ionic strength (e.g., I = 1.0 M).
• Kinetic Measurements: The reaction progress is monitored at specific temperatures (60, 70, and 80 °C) to determine the rate constants.
• Data Analysis: Rate data is analyzed to determine the mechanism and calculate thermodynamic parameters like activation enthalpy (ΔH≠) and entropy (ΔS≠).

Quantitative Data Summary

The following table consolidates the key numerical data from the study for easy reference [1]:

Table 1: Kinetic and Thermodynamic Parameters for the Anation Reaction

Table 2: First Acidity Constant (K_a) of H₃PO₃ at I=1.0

Experimental Workflow Diagram

The following diagram maps out the key stages of the experimental process, from problem identification to analysis and troubleshooting.

Experimental Troubleshooting Workflow

How to Use This Information

The workflow diagram provides a logical path for diagnosing issues. If you are facing a problem like low yield:

• Systematically follow the primary checks for temperature, acidity, and reactive species, as these are the most common failure points.
• If the problem persists, proceed to the advanced analysis stage, using the quantitative data in Table 1 to compare against your experimental results.
• The mechanism (I_d) and association constant are fundamental; significant deviations may indicate issues with reactant purity or experimental conditions.

References

• 1. Kinetics of the anation reaction of pentaamineaquacobalt(III) by... [link.springer.com]

Author: Smolecule Technical Support Team. Date: February 2026

Frequently Asked Questions

• Q1: What are the primary factors that cause phosphite degradation in solution? Phosphite (HPO₃²⁻) is susceptible to oxidation, primarily by dissolved oxygen, especially under certain catalytic conditions [1]. Key factors influencing its stability include:

  • Dissolved Oxygen: The most significant factor. Oxidation rates increase with higher oxygen concentrations [1].
  • Light and Radicals: Exposure to light, which can generate radical ions (e.g., ·OH), accelerates breakdown [1].
  • pH Level: The adsorption and stability of phosphite are influenced by the pH of the solution [1].
  • Metal Ions: The presence of certain metal ions, particularly iron in the form of Hydrous Ferric Oxides (HFO), can affect stability. Notably, HFO preferentially adsorbs phosphate over phosphite, which can influence the relative persistence of phosphite in experimental systems [1].

• Q2: What is the typical half-life of phosphite in aqueous solution? In the absence of biological activity, radical ions, and molecular oxygen, phosphite is kinetically stable with an estimated half-life of around 0.6 million years [1]. However, in the presence of oxygen and other catalysts, this rate can increase dramatically in lab settings.

• Q3: How can I prevent phosphite oxidation in my stock solutions?

  • Use anoxic preparation techniques inside an anaerobic chamber.
  • Sparge solutions with inert gases like argon or nitrogen to remove dissolved oxygen.
  • Store solutions in air-tight, dark containers.
  • Consider adjusting the pH to a level that minimizes catalytic reactions, as informed by your specific experimental matrix.

Key Experimental Data on Phosphite Adsorption

The following data, derived from studies on Hydrous Ferric Oxides (HFO), is critical for understanding phosphite behavior in systems containing iron minerals [1].

Table 1: Phosphite and Phosphate Adsorption Coefficients (Kads) on HFO

Table 2: Estimated Phosphite Concentrations During the Great Oxidation Event

Experimental Protocol: Phosphite Stability Assessment

This protocol outlines a method for evaluating phosphite stability in solution under various conditions.

Workflow Overview:

Materials:

• Sodium phosphite (Na₂HPO₃) stock solution of known concentration.
• Buffer solutions to cover a range of pH (e.g., 6.0 - 8.5).
• Gas-impermeable vials (e.g., crimp-top serum vials).
• Inert gas supply (Nitrogen or Argon, 99.99%).
• Ion Chromatography (IC) system or colorimetric assay kits for phosphite.

Procedure:

• Solution Preparation: Inside an anaerobic chamber, prepare a master solution of phosphite in your desired matrix (e.g., deionized water, artificial seawater). Split this solution and adjust different batches to target pH levels.
• Aliquot and Deoxygenate: Transfer solutions to gas-impermeable vials. For anoxic experiments, seal the vials and sparge the headspace with inert gas for at least 15 minutes. For oxic experiments, expose the solutions to air.
• Incubation: Incubate all vials under controlled temperature and light/dark conditions.
• Sampling and Analysis: At predetermined time points, sacrificially sample vials. For anoxic samples, perform sampling in an anaerobic chamber or using air-tight syringes. Filter samples if necessary and analyze phosphite concentration using Ion Chromatography or a specific colorimetric method.
• Data Calculation: Plot phosphite concentration over time. Use linear or non-linear regression to determine the degradation rate constant (k) and calculate the half-life (t₁/₂) using the formula: t₁/₂ = ln(2) / k.

Phosphite Pathways and Abiotic Interactions

The diagram below illustrates the key pathways influencing phosphite stability in a system containing iron, which is common in geological and laboratory contexts [1].

References

• 1. Bioavailable phosphite in the surface ocean during ... [nature.com]

Author: Smolecule Technical Support Team. Date: February 2026

Phosphorus Chemistry & Temperature Effects

The table below summarizes key information on phosphorus compounds, which provides context for understanding the behavior of phosphite (hydrogenphosphite) in experimental conditions.

Experimental Workflow for Temperature Influence

Based on the general principles found in the research, the following workflow outlines a systematic approach to investigate the effect of temperature on a process involving phosphite. You can adapt this to your specific production method.

Suggested Paths for Further Information

Since direct troubleshooting guides for "this compound production" were not available, I suggest these approaches to find more specific technical details:

• Refine Your Search Strategy: Search for the specific chemical synthesis method you are using, for example, "troubleshooting hydrolysis of P4O6" or "optimizing temperature for hypophosphite oxidation." The exact production route is critical.
• Consult Specialized Databases: Technical data for specific chemical reactions is often found in specialized sources. Search platforms like Reaxys or SciFinder for full experimental procedures, or delve into older inorganic chemistry synthesis handbooks.
• Analyze by Analogy: Use the stability information for hypophosphate [3] as a guide. If your product is unstable, consider whether the issue is disproportionation (favored in solution) or oxidation (favored at high heat).

References

• 1. Bioavailable phosphite in the surface ocean during ... [nature.com]
• 2. Contrasting the influences of phosphate and phosphite on ... [pmc.ncbi.nlm.nih.gov]
• 3. Implausibility of hypophosphate on the early Earth and today [link.springer.com]

Author: Smolecule Technical Support Team. Date: February 2026

HCl Scrubbing Method for Gaseous Streams

A highly effective method for removing HCl from gaseous streams uses Magnesium-Aluminum Oxide (Mg–Al oxide) [1]. This approach is particularly useful for handling HCl generated during reactions, such as the thermal degradation of PVC or other chlorinated compounds.

The table below summarizes the scrubbing process and its performance:

Synthesis Protocol: Calcium Hydrogen Phosphite

To illustrate a reaction that involves phosphites, here is a hydrothermal synthesis protocol for Calcium Hydrogen Phosphite (CaHPO₃), which does not produce HCl as a byproduct [2]. This provides a useful reference for handling phosphites under controlled conditions.

Workflow Overview: Calcium Hydrogen Phosphite Synthesis [2]

Procedure in Detail:

• Reactant Mixture: In a suitable container, dissolve 2.36 g of calcium nitrate tetrahydrate (Ca(NO₃)₂·4H₂O, 10.0 mmol), 0.52 g of phosphorous acid (H₃PO₃, 6.0 mmol), and 0.47 g of ammonium perchlorate (NH₄ClO₄, 4.0 mmol) in 10 ml of deionized water [2].
• Basification: Add 4.0 g of a 15 N ammonium hydroxide (NH₄OH) solution to the mixture [2].
• Reaction Vessel: Transfer the final mixture into a 23 ml Teflon-lined stainless steel pressure vessel (autoclave) [2].
• Heating: Place the sealed vessel in an oven and heat at 473 K (200 °C) for seven days [2].
• Cooling & Recovery: After seven days, allow the vessel to cool to room temperature over several hours. Caution: Follow standard safety procedures for handling hot pressurized vessels. Open the vessel and recover the solid product by vacuum filtration [2].
• Washing: Rinse the collected crystals with deionized water [2].
• Product: The result is sparkling, colorless prismatic crystals of CaHPO₃. The expected yield is approximately 93% based on the initial amount of calcium [2].

Troubleshooting Common Experimental Issues

Here are solutions to some frequently encountered problems:

Key Technical Considerations for Your Research

• Material Regeneration: The Mg–Al oxide scrubbing agent is a recyclable material. After saturation with HCl, the resulting Cl · Mg–Al LDH can be calcined to release concentrated HCl and regenerate the active Mg–Al oxide, making the process sustainable for lab-scale and industrial applications [1].
• Phosphite vs. Phosphate: Be aware that phosphites (P³⁺) are distinct from phosphates (P⁵⁺). They are reducing agents and can participate in different chemical and biochemical pathways. For instance, some microorganisms can use phosphite as a phosphorus source or even as an electron donor in energy metabolism (dissimilatory phosphite oxidation) [4].

References

• 1. Removal of hydrogen chloride from gaseous streams using ... [sciencedirect.com]
• 2. Synthesis and crystal structure of calcium hydrogen ... [pmc.ncbi.nlm.nih.gov]
• 3. US2862948A - Production of dialkyl hydrogen phosphites [patents.google.com]
• 4. Microbial Phosphite Oxidation and Its Potential Role in the ... [pubmed.ncbi.nlm.nih.gov]

Author: Smolecule Technical Support Team. Date: February 2026

The table below summarizes common impurities, their effects, and recommended removal methods to help you diagnose issues in your hydrogen phosphite materials [1] [2] [3].

Experimental Protocol: Purification of Hydrogen Phosphite Solutions

This protocol outlines a methodology for purifying hydrogen phosphite solutions, such as those derived from industrial phosphogypsum or synthesis by-products, by targeting metallic and soluble phosphorus impurities [2] [4].

1. Principle The purification process combines ion-exchange to remove cationic metal impurities like Fe³⁺ and selective precipitation followed by filtration to eliminate soluble phosphorus species [2] [4].

2. Materials

• Impure Hydrogen Phosphite Solution: e.g., a solution generated from an industrial process.
• Cation Exchange Resin: e.g., a strong acid gel type resin.
• Calcium Salts: e.g., Calcium Chloride (CaCl₂), analytical grade.
• Deionized Water
• Equipment: Beakers, stir plate, filtration setup (Buchner funnel & flask), pH meter, conductivity meter, ICP-OES for analysis.

3. Procedure

• Step 1: Ion Exchange (Metals Removal)

  • Pass the impure hydrogen phosphite solution slowly through a column packed with a strong acid cation exchange resin.
  • Monitor the effluent's conductivity. The resin will capture cationic impurities like Fe³⁺, Al³⁺, releasing H⁺ ions into the solution [4].
  • Collect the purified acidic eluent.

• Step 2: Soluble Phosphorus Precipitation

  • To the eluent from Step 1, add a calculated amount of a calcium salt (e.g., CaCl₂) under constant stirring.
  • Adjust the pH to neutral or slightly basic to facilitate the precipitation of soluble phosphorus as various forms of calcium phosphate [2].
  • Allow the precipitate to flocculate for several hours.

• Step 3: Filtration

  • Filter the mixture from Step 2 using a Buchner funnel to remove the precipitated calcium phosphates and any other co-precipitated solids.
  • The filtrate is your purified hydrogen phosphite solution.

• Step 4: Analysis & Verification

  • Analyze the final filtrate using ICP-OES to quantify the remaining levels of Fe, P, and other trace elements.
  • Compare the values against your target purity specifications.

The following workflow diagram illustrates the core procedural steps and decision points.

Frequently Asked Questions (FAQs)

Q1: Why is iron (Fe) impurity a significant concern in catalytic applications of hydrogen phosphites? Iron doping can drastically alter the local electronic structure of materials like nickel-iron hydrogen phosphites. While it may enhance activity for one reaction (e.g., Hydrogen Evolution Reaction), it can decrease activity for another (e.g., Urea Oxidation Reaction). Precise control over Fe content is therefore crucial for tuning catalytic performance [1].

Q2: What is the key difference between removing soluble versus insoluble phosphorus impurities? Soluble phosphorus impurities like H₃PO₄ require a chemical transformation, such as precipitation into an insoluble form (e.g., calcium phosphate) before physical removal. Insoluble phosphorus impurities, being solids already, can often be removed directly by physical methods like filtration or flotation [2] [3].

Q3: Are there safety considerations specific to handling hypophosphorous acid (H₃PO₂) during purification? Yes. Hypophosphorous acid is a powerful reducing agent. It should be stored in corrosion-resistant containers away from oxidizers. When heated above 110°C, it can disproportionation into phosphine (PH₃), a highly toxic gas, and phosphorous acid. Always use appropriate personal protective equipment (PPE) and work in a well-ventilated fume hood [5] [4].

References

• 1. Adjustable composition of nickel–iron hydrogen phosphite ... [sciencedirect.com]
• 2. Review of the State of Impurity Occurrences and ... [pmc.ncbi.nlm.nih.gov]
• 3. Influence of phosphorus impurities on the structure and ... [sciencedirect.com]
• 4. HYPOPHOSPHOROUS ACID (HPA) - Ataman Kimya [atamanchemicals.com]
• 5. Hypophosphorous acid [en.wikipedia.org]

Author: Smolecule Technical Support Team. Date: February 2026

Understanding Phosphite Solubility: Key Data

Phosphite (HPO₃²⁻) is a reduced form of phosphorus that is notably more soluble than the more common phosphate. The table below summarizes its core solubility characteristics based on current research.

Frequently Asked Questions & Troubleshooting

Here are answers to some specific questions you might encounter during your research.

Q1: Why is my phosphite solution precipitating, even though it's known to be highly soluble?

• Potential Cause: Interaction with Divalent Cations. While phosphite is highly soluble, the statement that it is "up to 1000 times more soluble than phosphate" specifically holds true in the presence of divalent metals [1]. If you are working in a system with high concentrations of cations like Ca²⁺ or Mg²⁺, precipitation of metal phosphite salts can still occur, though it is less favorable than phosphate precipitation.
• Troubleshooting Steps:
  • Check Water Purity: Ensure your solvent (e.g., deionized water) is free of contaminant divalent cations.
  • Analyze Buffer/Media: Review the composition of your buffers or growth media for high levels of Ca²⁺, Mg²⁺, or other metals.
  • Consider Complexing Agents: For critical experiments, you may need to use a low concentration of a chelating agent (e.g., EDTA) to sequester divalent cations, but ensure this does not interfere with your biological or chemical system.

Q2: How can I experimentally demonstrate the competitive solubility between phosphate and phosphite?

• Experimental Context: A key study investigated the relative removal of phosphate (P(V)) and phosphite (P(III)) from solution by their adsorption onto Hydrous Ferric Oxides (HFO), which are minerals like ferrihydrite [1].
• Core Methodology Summary:
  • Precipitation: HFO was precipitated in solutions with varying chemistries (deionized water, diluted artificial seawater, full artificial seawater) with and without dissolved silica, at different pH levels [1].
  • Observation: The study found that HFOs preferentially adsorb and remove phosphate over phosphite from the solution [1]. This means that in an environment where HFO is precipitating (simulating the deposition of Banded Iron Formations), phosphite remains in solution longer than phosphate.
  • Implication: This selective process could have led to the accumulation of bioavailable phosphite in ancient oceans, and can be a factor in modern iron-rich aqueous systems [1].

Experimental Workflow & Solubility Relationship

The following diagrams, generated using Graphviz, outline the general experimental workflow for studying phosphite and the relationship between its key properties.

Diagram 1: A basic workflow for preparing and troubleshooting a phosphite solution in the lab.

Diagram 2: The logical relationship between key properties of phosphite that lead to its accumulation in an environment.

References

• 1. Bioavailable phosphite in the surface ocean during ... [nature.com]

Author: Smolecule Technical Support Team. Date: February 2026

The table below categorizes key classes of phosphorus(V)-containing esters, which include hydrogenphosphite derivatives, based on a review of market-approved drugs and compounds in clinical studies [1].

Experimental Hydrolysis Data & Protocols

Hydrolysis stability is a critical parameter in drug design. The following table summarizes experimental data and conditions for the hydrolysis of various P-esters, primarily compiled from a 2021 review [2].

Detailed Experimental Protocol: Acidic Hydrolysis of Phosphinates/Phosphonates [2] A common procedure for acidic hydrolysis is as follows:

• Reaction Setup: The phosphinate or phosphonate ester (e.g., 3 g) is placed in a round-bottom flask equipped with a reflux condenser.
• Acid Addition: A large excess of concentrated hydrochloric acid (e.g., 20 mL) is added to the flask.
• Heating: The mixture is heated to reflux with stirring.
• Monitoring: The reaction is typically monitored by TLC (Thin-Layer Chromatography) and can require 1.5 to 4 hours for phosphinates and potentially longer for phosphonates.
• Work-up: After completion, the mixture is cooled. The desired phosphinic or phosphonic acid often precipitates out upon cooling and can be collected by filtration. If necessary, the product can be further purified by recrystallization.

Analytical Methods for Characterization

Accurate determination of phosphorus compounds in complex matrices is non-trivial. The table below compares common analytical techniques [3].

Biological Relevance & Signaling Pathways

Phosphorus esters play fundamental roles in biology. Organophosphorus esters are involved in ubiquitous biochemical processes, including bioenergy and signal transductions, and are constituents of genetic material [4]. The reactivity of these compounds is crucial to their function.

The diagram below illustrates the central role of Reactive Oxygen Species (ROS) in mediating cell death, a key pathway where cellular stress signals can be triggered, and which some pharmaceutical agents aim to target [5].

Pharmaceutical Applications

Phosphorus-containing functional groups are a cornerstone in medicinal chemistry, primarily used in two strategies [1]:

• Prodrugs: Phosphoester prodrugs (phosphomonoesters) are designed to overcome poor solubility or permeability of parent drugs. The phosphate group is cleaved in vivo by enzymes like alkaline phosphatase to release the active drug [1].
• Biomimetics: Many drugs are analogues of endogenous phosphates. For example, Sofosbuvir is a nucleotide analogue for hepatitis C, and Remdesivir is a nucleotide analog used against COVID-19 [1].

References

• 1. Development and Clinical Application of Phosphorus ... [pmc.ncbi.nlm.nih.gov]
• 2. The Hydrolysis of Phosphinates and Phosphonates [pmc.ncbi.nlm.nih.gov]
• 3. Determination of phosphorus compounds in plant tissues: from... [plantmethods.biomedcentral.com]
• 4. Solvent and solvation effects on reactivities ... [pmc.ncbi.nlm.nih.gov]
• 5. sciencedirect.com/science/article/pii/S0167488916302324 [sciencedirect.com]

Author: Smolecule Technical Support Team. Date: February 2026

Analytical Techniques for Phosphite Compounds

The table below summarizes analytical techniques identified in the search results for studying phosphite and related compounds:

Framework for Analytical Method Validation

For validating an analytical method for hydrogenphosphite, you should follow established regulatory guidelines such as ICH Q2(R1) [5]. The following workflow outlines the core parameters and process.

Here are the typical acceptance criteria for these key validation parameters [6] [5]:

• Accuracy: Percent recovery should typically be between 98% and 102%.
• Precision: The relative standard deviation (%RSD) for repeatability and intermediate precision should generally be not more than 2.0%.
• Linearity: The coefficient of determination (r²) should be greater than 0.999 for the calibration curve.
• Specificity: The method must be able to measure the analyte without interference from other components like impurities or excipients.

Research Insights and Practical Paths Forward

To advance your project, here are the most relevant insights from current research and suggestions for next steps:

• Consider the Application Context: The identified techniques are used in very specific contexts. MST and ITC are powerful for studying binding events in biochemistry [1], while XPS and QCM are highly specialized for surface interaction studies in materials science [2].
• Leverage General Validation Principles: Since a direct guide for this compound is not available, the framework provided by ICH Q2(R1) [5] is your most reliable tool. You can adapt this general framework to your specific compound and analytical technique (e.g., HPLC or IC-ICP-MS).
• Investigate Foundational Resources: The dataset regarding IC-ICP-MS method validation for phosphite analysis [4] appears to be a highly relevant resource. You may find detailed protocols and validation data by accessing this dataset through the provided link.

References

• 1. The molecular basis of phosphite and hypophosphite ... [pmc.ncbi.nlm.nih.gov]
• 2. Combined ab initio and experimental study of phosphorus ... [arxiv.org]
• 3. HSPiP, Computational Modeling, and QbD-Assisted ... [pmc.ncbi.nlm.nih.gov]
• 4. of IC-ICPMS with chlorine removal for Method ... validation phosphite [data.gov.uk]
• 5. in Pharmaceuticals | Pharmaguideline Analytical Method Validation [pharmaguideline.com]
• 6. Analytical Method Validation Protocol for Pharmaceuticals [pharmaguideline.com]

Author: Smolecule Technical Support Team. Date: February 2026

IC/MS/MS Method for Phosphite Quantification

This method, developed for environmental and chemical analysis, provides a robust approach for quantifying phosphite with high sensitivity and accuracy using an ¹⁸O-labeled HPO₃²⁻ internal standard [1].

The workflow and detailed protocol are summarized in the diagram and table below.

Figure 1: IC/MS/MS Workflow for Phosphite Analysis. The workflow involves sample separation via Ion Chromatography, followed by selective detection using tandem Mass Spectrometry. The ¹⁸O-labeled internal standard (in red) is added early to correct for sample loss and matrix effects [1].

Interpretation and Adaptation for Validation

To adapt this method for spectroscopic validation in a pharmaceutical context, consider the following points:

• Core Principle: The combination of chromatographic separation with mass spectrometric detection is a gold standard for validating analytical methods due to its high specificity and sensitivity [1].
• Key for Validation: The use of a stable isotope-labeled internal standard is a robust strategy to achieve high accuracy and precision, which are critical for method validation according to guidelines like ICH Q2(R2).
• Potential Adaptations: While this specific protocol uses Ion Chromatography, you could explore coupling Liquid Chromatography (LC) with MS/MS for analyzing organic phosphite salts or prodrugs. The fundamental principles of internal standardization and MS/MS detection would remain the same [2].

References

• 1. Determination of phosphite (HPO 3 −2 ) by a new IC/MS ... [sciencedirect.com]
• 2. Identifying Novel Signaling Pathways: An Exercise Scientists ... [pmc.ncbi.nlm.nih.gov]

Author: Smolecule Technical Support Team. Date: February 2026

Thermal Stability Assays for Drug Discovery

The Cellular Thermal Shift Assay (CETSA) and related methods are central to modern drug discovery for measuring target engagement and protein thermal stability in a label-free manner [1] [2]. The core principle is that a ligand binding to a target protein often enhances the protein's thermal stability, which can be quantified as a shift in its melting temperature (Tm) [1].

The table below compares the main thermal shift assay formats based on your search results.

Experimental Protocol Overview

A general workflow for thermal shift assays is outlined below. Specific details such as buffer composition, heating rate, and detection method vary between DSF and CETSA [1] [2].

Key Experimental Considerations

• Buffer Conditions: The target protein must be stable, soluble, and not aggregated at ambient temperature in the chosen buffer. Incompatible additives (e.g., detergents in DSF) can interfere [2].
• Temperature Gradient: A suitable temperature range must be established to capture the protein's full melting curve [1].
• Detection Method:
  • DSF: Uses a polarity-sensitive dye (e.g., SyproOrange) [2].
  • CETSA (Western Blot): Relies on protein-specific antibodies [1].
  • MS-CETSA: Uses mass spectrometry for proteome-wide quantification [1].
• Data Interpretation: A positive shift in the protein's melting temperature (Tm) indicates a direct physical interaction between the small molecule and the target protein [1] [2].

References

• 1. Applications of the Cellular Thermal Shift Assay to Drug ... [pmc.ncbi.nlm.nih.gov]
• 2. Thermal shift assays in drug discovery – Troubleshooting ... [sciencedirect.com]

Author: Smolecule Technical Support Team. Date: February 2026

The following table summarizes three distinct protocols for synthesizing hydrogen phosphite compounds, ranging from simple inorganic salts to complex bimetallic electrocatalysts.

Detailed Experimental Protocols

For researchers looking to replicate these syntheses, here are the expanded methodological details.

Protocol 1: Hydrothermal Synthesis of CaHPO₃ [1]

This method is ideal for growing high-quality single crystals for structural determination.

• Solution Preparation: Dissolve 2.36 g of Ca(NO₃)₂·4H₂O (10.0 mmol), 0.52 g of H₃PO₃ (6.0 mmol), and 0.47 g of NH₄ClO₄ (4.0 mmol) in 10 mL of deionized water.
• Basification: Add 4.0 g of a concentrated ammonium hydroxide solution (15N) to the mixture.
• Reaction Vessel: Transfer the final mixture into a 23 mL Teflon-lined cup, which is then sealed inside a stainless steel pressure vessel.
• Heating and Crystallization: Heat the vessel in an oven at 473 K (200 °C) for 7 days.
• Product Recovery: After cooling to room temperature, recover the crystals by vacuum filtration and rinse them thoroughly with deionized water.

Protocol 2: Electrodeposition of NixFe1-x(H2PO2)2 Electrocatalysts [2]

This modern method produces amorphous materials with tunable properties for electrochemistry.

• Key Feature: This is a one-step electrodeposition process where Ni²⁺, Fe³⁺, and H₂PO₂⁻ ions from the solution are simultaneously co-deposited onto a conductive substrate, typically nickel foam [2].
• Material Characteristics: The resulting material lacks long-range order, forming an amorphous structure. This amorphous nature, combined with the three-dimensional porous architecture of the nickel foam, provides numerous active sites for electrocatalysis [2].
• Composition Tuning: The composition (the value of x in NiₓFe₁₋ₓ(H₂PO₂)₂) and thus the electronic properties can be adjusted by varying the ratio of metal ions in the deposition solution, allowing for performance optimization [2].

Application and Performance Data

For your comparison guides, the experimental performance of these synthesized compounds is crucial. The bimetallic nickel-iron hydrogen phosphite shows significant promise in energy applications.

• Electrocatalytic Performance: When tested for the Hydrogen Evolution Reaction (HER) in alkaline conditions, the bimetallic catalyst Ni₀.₇Fe₀.₃(H₂PO₂)₂ achieved a low overpotential of 92 mV to reach a current density of 10 mA cm⁻², indicating high efficiency [2].
• Comparison to Baseline: The activity of this bimetallic phosphite was superior to its iron-free counterpart, Ni(H₂PO₂)₂. This performance enhancement is attributed to iron doping, which modulates the local electronic structure of nickel and optimizes the adsorption energy of reaction intermediates [2].

Guide to Protocol Validation

When validating these or any new synthesis protocols, consider the following steps based on the practices evident in the literature:

• Reproducibility: Precisely follow the reported quantities, temperatures, and reaction durations. The hydrothermal synthesis, for example, requires strict adherence to the 7-day crystallization period [1].
• Material Characterization: Confirm the success of your synthesis using standard analytical techniques. The studies cited used X-ray Powder Diffraction to verify the amorphous nature of electrodeposited catalysts [2] and the crystalline structure of the hydrothermal product [1].
• Performance Validation: For functional materials like electrocatalysts, replicate the reported electrochemical tests to compare your product's performance against the published data [2].

Synthesis Workflow Diagrams

To help visualize the two main synthesis pathways, the following diagrams outline the key steps.

References

• 1. Synthesis and crystal structure of calcium hydrogen ... [pmc.ncbi.nlm.nih.gov]
• 2. Adjustable composition of nickel–iron hydrogen phosphite ... [sciencedirect.com]
• 3. US2862948A - Production of dialkyl hydrogen phosphites [patents.google.com]