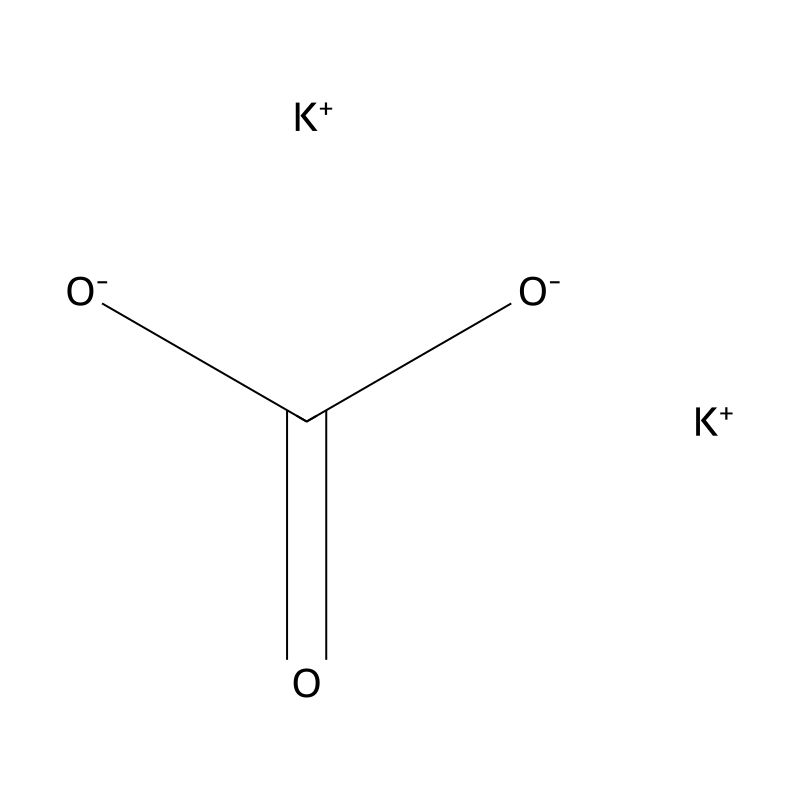
Potassium carbonate
CK2O3
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
CK2O3
Molecular Weight
InChI
InChI Key
SMILES
Solubility
For more Solubility (Complete) data for POTASSIUM CARBONATE (6 total), please visit the HSDB record page.
Insoluble in alcohol and acetone
111 g/100 g water at 25 °C
Soluble in 1 part cold, 0.7 part boiling water.
Solubility in water (g K2CO3/100 g H2O): 105.5 at 0 °C; 108.0 at 10 °C; 110.5 at 20 °C; 113.7 at 30 °C; 155.7 at 100 °C
Solubility in water, g/100ml at 20 °C: 112
Synonyms
Canonical SMILES
Organic Chemistry:
- Synthesis of Organic Compounds: Potassium carbonate acts as a strong base in various organic reactions, promoting deprotonation and facilitating the creation of carbon-carbon and carbon-heteroatom bonds. Studies utilize it in the synthesis of diverse compounds, including pharmaceuticals, agrochemicals, and specialty materials.
- Decarboxylation Reactions: Potassium carbonate can remove carboxylic acid functional groups from organic molecules, enabling the formation of alkanes, alkenes, and other valuable intermediates. This property is crucial in the research and development of novel organic molecules.
Materials Science:
- Electrolyte for Solid-State Batteries: Research explores the potential of potassium carbonate as a solid electrolyte material for next-generation lithium-ion batteries. Its high ionic conductivity and stability offer promising avenues for improving battery performance and safety [].
- Synthesis of Functional Materials: Potassium carbonate is used in the preparation of various functional materials, including ceramic pigments, catalysts, and precursors for advanced electronic materials. Its versatility makes it a valuable tool for material scientists exploring novel functionalities.
Environmental Science:
- Carbon Capture and Storage: Potassium carbonate solutions are being investigated for their ability to capture carbon dioxide (CO₂) from industrial emissions. The captured CO₂ can then be stored underground, potentially mitigating its impact on climate change.
- Wastewater Treatment: Potassium carbonate serves as a pH regulator and precipitant in wastewater treatment processes. It can help remove heavy metals, phosphates, and other contaminants from industrial wastewater streams.
Biomedical Research:
- Cell Culture Media Supplement: Potassium carbonate is often included in cell culture media to maintain a suitable pH and provide essential potassium ions for cell growth and function.
- Drug Discovery and Development: Researchers utilize potassium carbonate in various assays and screening platforms to assess the efficacy and safety of potential drug candidates.
Potassium carbonate, with the chemical formula K₂CO₃, is an inorganic compound also known as carbonate of potash, pearl ash, or dipotassium carbonate. It appears as a hygroscopic and deliquescent white powder that is odorless and has an alkaline taste. Potassium carbonate is highly soluble in water, forming a strongly alkaline solution with a pH of approximately 11.6. It is primarily derived from the ashes of plants that contain potassium and is a key component of potash, historically used in various applications such as soap and glass production .
- Reaction with Acids: When potassium carbonate reacts with hydrochloric acid, it undergoes a double displacement reaction:This reaction produces potassium chloride, water, and carbon dioxide gas2.
- Decomposition of Potassium Bicarbonate: Potassium carbonate can also be synthesized from potassium bicarbonate through thermal decomposition:
- Base Reactions: As a weak base, potassium carbonate can deprotonate weak acids such as phenols and dicarbonyl compounds, facilitating various organic reactions .
Potassium carbonate has limited direct biological activity but plays a role in various biochemical processes. It acts as a buffering agent in biological systems, helping to maintain pH levels. Its mild alkalinity makes it useful in food processing and fermentation, particularly in wine and mead production where it stabilizes acidity . Additionally, it is non-toxic at low concentrations but can cause irritation upon contact with skin or eyes.
Potassium carbonate can be synthesized through several methods:
- Reaction with Carbon Dioxide: The most common commercial method involves reacting potassium hydroxide with carbon dioxide:
- From Potassium Chloride: Another method involves treating potassium chloride with carbon dioxide in the presence of an organic amine to yield potassium bicarbonate, which is then heated to produce potassium carbonate:
- Historical Methods: Historically, potassium carbonate was produced by baking plant ashes (potash) in kilns to remove impurities .
Potassium carbonate has diverse applications across various industries:
- Glass and Soap Production: It is widely used in the manufacture of glass and as a key ingredient in soap making due to its alkaline properties.
- Food Industry: Utilized as a leavening agent in baking and as a buffering agent in wine production.
- Agriculture: Employed as a source of potassium for fertilizers.
- Fire Suppression: Acts as a fire suppressant in certain applications.
Potassium carbonate shares similarities with other alkali metal carbonates but exhibits unique properties that distinguish it:
| Compound | Chemical Formula | Solubility in Water | Unique Features |
|---|---|---|---|
| Sodium Carbonate | Na₂CO₃ | Highly soluble | Commonly used for cleaning; known as soda ash |
| Calcium Carbonate | CaCO₃ | Low solubility | Used extensively in construction and agriculture |
| Ammonium Carbonate | (NH₄)₂CO₃ | Soluble | Often used in baking; decomposes to ammonia |
| Lithium Carbonate | Li₂CO₃ | Soluble | Used in psychiatric medications for mood stabilization |
Potassium carbonate stands out due to its high solubility in water compared to calcium carbonate and its application versatility across food processing and chemical synthesis that may not be applicable to other carbonates .
Advanced Carbonation Techniques for Potassium Hydroxide Solutions
Subatmospheric Pressure Optimization in Continuous Reactor Systems
Industrial-scale carbonation of potassium hydroxide (KOH) with carbon dioxide (CO₂) is enhanced through subatmospheric pressure conditions. The Neumann process, patented in 1973, operates at 80–135°C and 130 torr (17.3 kPa), enabling continuous potassium carbonate hydrate production [1]. Under reduced pressure, water evaporation occurs concurrently with CO₂ absorption, maintaining optimal reaction stoichiometry while preventing equipment corrosion [1] [2].
A critical advantage of subatmospheric systems is the reduction of energy required for solvent evaporation. At 130 torr, the boiling point of water decreases to approximately 55°C, allowing efficient vapor removal without excessive heating [1]. This configuration achieves 85–92% potassium conversion rates in commercial reactors, with residual KOH concentrations below 0.5% [2]. Continuous systems employ cascading reactor designs where pressure gradients between stages drive simultaneous carbonation and crystallization [1] [3].
Table 1: Performance Metrics of Subatmospheric Carbonation
| Parameter | Value Range | Source |
|---|---|---|
| Operating Pressure | 100–200 torr | [1] |
| Reaction Temperature | 80–135°C | [1] |
| KOH Conversion Efficiency | 85–92% | [2] |
| Hydrate Purity | 98–99.5% | [3] |
Hydrate Crystallization Dynamics Under Controlled Evaporation
Crystallization of K₂CO₃·1.5H₂O from saturated solutions requires precise control of evaporation rates and supersaturation levels. Industrial processes utilize mixed suspension mixed product removal crystallizers to maintain steady-state conditions [2] [3]. In these systems, mother liquor recycling stabilizes the metastable zone width (MZW), the temperature-concentration range where spontaneous nucleation is avoided [5].
Experimental data reveal that evaporation rates exceeding 2.5 kg/m²·min induce dendritic crystal growth, reducing filterability [6]. Optimal operation occurs at 1.2–1.8 kg/m²·min, producing monoclinic crystals with 200–300 μm median particle sizes [3] [6]. The hydration state of precipitated crystals depends on the cooling profile: rapid quenching (5°C/min) yields K₂CO₃·1.5H₂O, while gradual cooling (1°C/min) forms K₂CO₃·0.5H₂O [5].
Solid-Phase Dehydration Mechanisms of Potassium Carbonate Sesquihydrate
Nucleation-Growth Kinetics in Anhydrous Phase Formation
Dehydration of K₂CO₃·1.5H₂O to anhydrous K₂CO₃ follows Avrami-Erofeev kinetics, with an activation energy of 68.5 kJ/mol [2]. In fluidized bed reactors, the process occurs in two stages:
- Lattice Water Removal (110–130°C): Bound water molecules detach, forming intermediate amorphous phases [4].
- Crystallographic Rearrangement (130–160°C): Recrystallization into anhydrous orthorhombic structure [3] [4].
Particle size significantly impacts dehydration rates. Granules below 100 μm complete dehydration in 8–12 minutes at 140°C, whereas 500 μm particles require 25–30 minutes due to intra-particle diffusion limitations [4].
Supersaturation Thresholds in Industrial-Scale Dehydration
Supersaturation ratio (S) governs nucleation frequency in anhydrous K₂CO₃ production. For the reaction:
$$ \text{K}2\text{CO}3\cdot1.5\text{H}2\text{O} \rightarrow \text{K}2\text{CO}3 + 1.5\text{H}2\text{O} $$
The critical supersaturation threshold is $$ S_{\text{crit}} = 1.25 $$, beyond which secondary nucleation dominates crystal size distribution [5] [6]. Industrial fluidized bed systems maintain $$ S = 1.05–1.15 $$ through real-time conductivity monitoring and adjusted heating rates [4] [6].
Table 2: Dehydration Process Parameters
| Parameter | Value Range | Source |
|---|---|---|
| Calcination Temperature | 130–160°C | [3] |
| Critical Supersaturation | 1.25 | [5] |
| Optimal Particle Size | 100–300 μm | [4] |
| Residence Time | 10–30 minutes | [4] |
Physical Description
White, very deliquescent powder.; The hydrate occurs as small, white, translucent crystals or granules
White deliquescent powder; [Hawley] Available as a solid (anhydrous or sesquihydrate) and concentrated solution (47% potassium carbonate); [CHEMINFO]
COLOURLESS HYGROSCOPIC CRYSTALS OR HYGROSCOPIC WHITE POWDER.
Color/Form
Granules or granular powder
White, deliquescent, granular, translucent powde
Hydrogen Bond Acceptor Count
Exact Mass
Monoisotopic Mass
Boiling Point
Heavy Atom Count
Taste
Density
2.29 g/cm³
Odor
Decomposition
Melting Point
891 °C
UNII
GHS Hazard Statements
Reported as not meeting GHS hazard criteria by 25 of 3091 companies. For more detailed information, please visit ECHA C&L website;
Of the 54 notification(s) provided by 3066 of 3091 companies with hazard statement code(s):;
H302 (17.42%): Harmful if swallowed [Warning Acute toxicity, oral];
H315 (52.64%): Causes skin irritation [Warning Skin corrosion/irritation];
H319 (98.89%): Causes serious eye irritation [Warning Serious eye damage/eye irritation];
H335 (49.61%): May cause respiratory irritation [Warning Specific target organ toxicity, single exposure;
Respiratory tract irritation];
Information may vary between notifications depending on impurities, additives, and other factors. The percentage value in parenthesis indicates the notified classification ratio from companies that provide hazard codes. Only hazard codes with percentage values above 10% are shown.
Therapeutic Uses
ALKALIZER; DIURETIC AGENT
MEDICATION (VET): DEGREASING AGENT, KERATIN SOFTENER
For the temporary relief of symptoms due to constipation: abdominal bloating, abdominal discomfort, irregularity of bowel movements. ... Disclaimer: This homeopathic product has not been evaluated by the Food and Drug Administration for safety or efficacy. FDA is not aware of scientific evidence to support homeopathy as effective.
Pictograms
Irritant
Impurities
Other CAS
Associated Chemicals
Wikipedia
Androsterone
Use Classification
Safer Chemical Classes -> Green circle - The chemical has been verified to be of low concern
Food additives
Food Additives -> ACIDITY_REGULATOR; -> JECFA Functional Classes
Cosmetics -> Buffering
Methods of Manufacturing
Alkyl amines or ion-exchange resins can be used with potassium chloride and carbon dioxide to yield potassium bicarbonate which is calcined to the carbonate.
Except for small amounts produced by obsolete processes, e.g. the leaching of wood ashes and the Engel-Precht process, potassium carbonate is produced by the carbonation, i.e., via reaction with carbon dioxide, of potassium hydroxide.
Potassium carbonate... is produced by the following methods of manufacture: (1) By electrolysis of potassium chloride followed by exposing the resultant potassium to carbon dioxide; (2) By treating a solution of potassium hydroxide with excess carbon dioxide to produce potassium carbonate; (3) By treating a solution of potassium hydroxide with carbon dioxide to produce potassium bicarbonate, which is then heated to yield potassium carbonate.
For more Methods of Manufacturing (Complete) data for POTASSIUM CARBONATE (6 total), please visit the HSDB record page.
General Manufacturing Information
Fabricated Metal Product Manufacturing
Food, beverage, and tobacco product manufacturing
All Other Basic Organic Chemical Manufacturing
Other (requires additional information)
Soap, Cleaning Compound, and Toilet Preparation Manufacturing
Paint and Coating Manufacturing
Not Known or Reasonably Ascertainable
All Other Basic Inorganic Chemical Manufacturing
Mining (except Oil and Gas) and support activities
Primary Metal Manufacturing
Wholesale and Retail Trade
Non-metallic Mineral Product Manufacturing (includes clay, glass, cement, concrete, lime, gypsum, and other non-metallic mineral product manufacturing)
Plastics Material and Resin Manufacturing
Miscellaneous Manufacturing
Synthetic Rubber Manufacturing
Paper Manufacturing
Pesticide, Fertilizer, and Other Agricultural Chemical Manufacturing
Pharmaceutical and Medicine Manufacturing
All Other Chemical Product and Preparation Manufacturing
Oil and Gas Drilling, Extraction, and Support activities
Carbonic acid, potassium salt (1:2): ACTIVE
It has been added to...skin ointments & lotions to aid contact with affected areas or skin penetration of active ingredients by dissolving keratin, sebaceous matter, or skin greases.
The cost of producing potassium carbonate is four to five times greater than that of producing sodium carbonate. Thus sodium carbonate is almost always used for applications in which the two carbonates are equivalent chemically.
In Anglo-American usage, the term potash today includes potassium carbonate as well as all potassium salts, such as KCl, K2SO4, K2SO4.MgSO4.xH2O that are used as fertilizers; the potassium content is given as K2O.
Potash is an impure form of potassium carbonate mixed with other potassium salts obtained by leaching wood ash. Pearl ash is a purer form of potassium carbonate.
Storage Conditions
Potassium carbonate is stored in bunkers; the ventilation air must be dry because of the hydroscopicity of the product.
Keep container tightly closed in a dry and well-ventilated place.
Interactions
Dates
Explore Compound Types
