Lithium sulfate

Lithium sulfate (Li₂SO₄) is a white, crystalline inorganic salt []. It is the lithium salt of sulfuric acid, a common industrial chemical. Lithium sulfate occurs naturally in mineral deposits but is also produced commercially through various processes []. Due to its unique properties, lithium sulfate finds applications in diverse scientific research fields, including material science, pharmaceuticals, and analytical chemistry [, ].

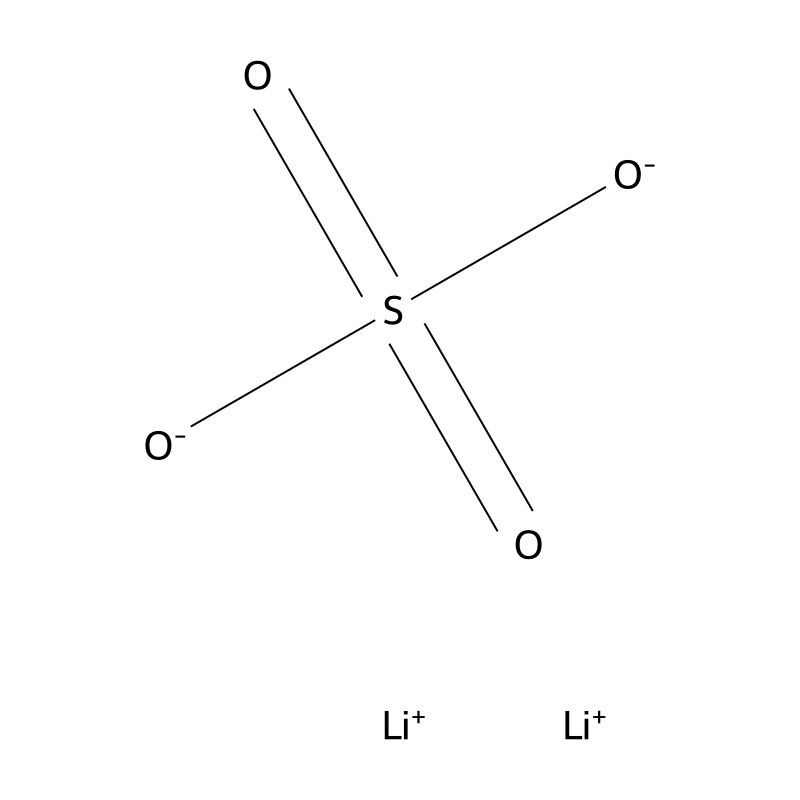
Molecular Structure Analysis

Lithium sulfate adopts a tetrahedral structure. Each lithium cation (Li⁺) is surrounded by four oxygen anions (O²⁻) from four sulfate anions (SO₄²⁻). The sulfur atom (S⁶⁺) in the sulfate ion is bonded to four oxygen atoms in a tetrahedral arrangement. This structure allows for strong ionic bonding between the lithium and sulfate ions, contributing to the stability of the compound [].

Chemical Reactions Analysis

Synthesis:

Lithium sulfate can be synthesized through several methods. A common industrial process involves the reaction between lithium carbonate (Li₂CO₃) and sulfuric acid (H₂SO₄) [].

Li₂CO₃ (s) + H₂SO₄ (aq) → Li₂SO₄ (aq) + CO₂ (g) + H₂O (l) []

Decomposition:

At high temperatures (above 859°C), lithium sulfate decomposes into lithium oxide (Li₂O) and sulfur trioxide (SO₃) [].

Li₂SO₄ (s) → Li₂O (s) + SO₃ (g) []

Other Reactions:

Lithium sulfate can react with other metal salts to form double sulfates. For example, it reacts with potassium chloride (KCl) to form potassium lithium sulfate (KLiSO₄) [].

Li₂SO₄ (aq) + 2 KCl (aq) → 2 KLiSO₄ (s) []

Physical and Chemical Properties

• Formula: Li₂SO₄
• Molar mass: 109.94 g/mol []
• Melting point: 859°C []
• Boiling point: Decomposes above 859°C []
• Solubility: Soluble in water (340 g/L at 25°C), insoluble in ethanol, acetone, and pyridine []
• Density: 2.22 g/cm³ (anhydrous) []
• Stability: Stable under normal conditions []

Mechanism of Action (Not Applicable)

Lithium sulfate does not have a specific biological mechanism of action. However, its hygroscopic nature (ability to absorb moisture) can be exploited in desiccant applications for scientific research [].

Protein Crystallization:

• Lithium sulfate is a crucial component in protein crystallization experiments, a vital technique for determining protein structures and functions. It acts as a precipitating agent, promoting the formation of well-ordered crystals suitable for X-ray diffraction analysis .
• Researchers use different concentrations of lithium sulfate solutions to create various precipitation conditions, promoting crystal formation for different proteins .

Neuroscience Research:

• Studies have explored the potential of lithium sulfate as a neuromodulator, influencing neuronal activity and behavior. Its role in regulating signaling pathways and neurotransmitter levels is under investigation .
• Research suggests that lithium sulfate may have therapeutic potential in treating neurological disorders like bipolar disorder and Alzheimer's disease, although further research is necessary to establish its efficacy and safety .

Material Science and Battery Research:

• Lithium sulfate's unique properties, including its ionic conductivity and thermal stability, make it a potential candidate for developing solid-state electrolytes in next-generation batteries .
• Researchers are investigating lithium sulfate as a component in solid-state electrolytes, aiming to overcome limitations of traditional liquid electrolytes in lithium-ion batteries, such as flammability and limited lifespan .

Ultrasound Technology:

• Due to its piezoelectric properties, lithium sulfate crystals can convert mechanical energy into electrical signals and vice versa. This makes them valuable as ultrasound receivers in non-destructive testing applications .
• Researchers utilize lithium sulfate crystals in the development of transducers for medical ultrasound imaging and other non-destructive testing methods .