Cerium trifluoride
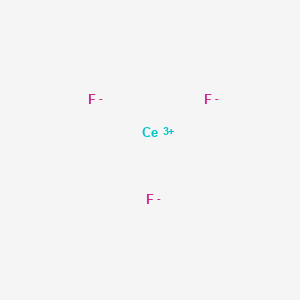
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Synonyms
Canonical SMILES
Cerium fluoride offers several advantages over other scintillator materials, making it particularly valuable in various scientific research applications:
- High light yield: CeF3 crystals exhibit a high light yield, meaning they produce a significant amount of light for each absorbed photon of radiation. This high sensitivity allows for the detection of even weak radiation signals.
- Fast decay time: The decay time refers to the time it takes for the emitted light to die out after the radiation interaction. Cerium fluoride features a fast decay time, typically in the nanosecond range, enabling efficient detection and accurate timing measurements of radiation events. This is crucial in applications like nuclear physics studies and time-resolved spectroscopy.
- Good energy resolution: Cerium fluoride crystals possess good energy resolution, meaning they can effectively distinguish between different energies of incoming radiation. This allows for the identification and characterization of various radiation sources in a sample.
These properties make cerium fluoride crystals valuable in various scientific research fields, including:
- Nuclear physics: Studying the properties of atomic nuclei, their reactions, and decay processes.
- Medical imaging: Positron emission tomography (PET) and single-photon emission computed tomography (SPECT) are medical imaging techniques that utilize scintillation detectors to image the distribution of radiopharmaceuticals within the body for diagnosis and treatment purposes.
- Material science: Analyzing the elemental composition and structure of materials using techniques like X-ray fluorescence (XRF) and neutron activation analysis (NAA).
- Environmental science: Studying the presence and distribution of radioactive contaminants in the environment using X-ray fluorescence (XRF) and gamma spectroscopy.
Other Scientific Research Applications
Beyond its role in scintillation detectors, cerium fluoride is being explored for other scientific research applications due to its unique properties:
- Upconversion luminescent material: Cerium fluoride nanoparticles exhibit upconversion luminescence, where they can convert lower-energy photons (e.g., infrared) into higher-energy photons (e.g., visible light). This property holds potential for applications in bioimaging, solar cells, and displays.
- Catalyst: Cerium fluoride demonstrates catalytic activity in various reactions, including hydrogen production, water splitting, and organic synthesis.
- Biomedical applications: Research suggests potential applications of cerium fluoride nanoparticles in biomedicine, such as radiosensitizers in cancer therapy and antioxidants for protecting cells from oxidative stress. However, further research is needed to fully understand their safety and efficacy in these contexts.
Cerium trifluoride is an inorganic compound with the chemical formula CeF₃. It is a member of the lanthanide series and is characterized by its white crystalline appearance. Cerium trifluoride has a molecular weight of approximately 197.11 g/mol and is known for its low solubility in water, which makes it useful in various applications where moisture resistance is necessary . The compound exhibits a hexagonal crystal structure and is typically produced in a powdered form.
- Mild irritant: Exposure to cerium fluoride dust or fumes may cause irritation to the eyes, skin, and respiratory system.
- Fluoride compound: Ingestion of cerium fluoride can lead to fluoride poisoning, similar to other fluoride compounds. Symptoms may include nausea, vomiting, and abdominal pain.
- Formation of Cerium Tetrafluoride: At elevated temperatures (above 523 K), cerium trifluoride reacts with elemental fluorine to form cerium tetrafluoride (CeF₄) according to the reaction:This reaction highlights the compound's reactivity under specific conditions .
- Reduction Reactions: Cerium trifluoride can be reduced to cerium oxide or cerium metal through reactions with reducing agents such as hydrogen or ammonia, especially at high temperatures .
- Hydrolysis: In the presence of water vapor, cerium trifluoride can hydrolyze, leading to the formation of cerium hydroxide and hydrogen fluoride:
The synthesis of cerium trifluoride can be achieved through various methods:
- Solid-State Reaction: A common method involves the reaction between cerium dioxide (CeO₂) and ammonium bifluoride (NH₄HF₂) under controlled conditions. The process typically occurs at elevated temperatures (around 380 K) and requires careful handling to avoid moisture contamination .
- Hydrothermal Synthesis: This method utilizes high-pressure and high-temperature water solutions to promote the formation of cerium trifluoride from cerium salts and fluoride sources.
- Chemical Vapor Deposition: This technique involves the deposition of cerium fluoride onto substrates from gaseous precursors, allowing for the production of thin films or coatings.
Interaction studies involving cerium trifluoride focus on its behavior in various environments and with different substances:
- Reactivity with Water: Studies have shown that cerium trifluoride can hydrolyze when exposed to moisture, affecting its stability and reactivity.
- Complex Formation: Cerium trifluoride can form complexes with other ions, influencing its solubility and transport properties in aqueous solutions.
- Kinetic Studies: Research has been conducted on the kinetics of reactions involving cerium trifluoride, particularly concerning its conversion to other fluorides like cerium tetrafluoride .
Cerium trifluoride shares similarities with other lanthanide fluorides but possesses unique characteristics that distinguish it:
| Compound | Formula | Unique Properties |
|---|---|---|
| Cerium Fluoride | CeF₃ | Low solubility in water; reacts with fluorine |
| Cerium Tetrafluoride | CeF₄ | Higher solubility; more reactive than CeF₃ |
| Lanthanum Trifluoride | LaF₃ | Similar crystal structure but different reactivity |
| Neodymium Trifluoride | NdF₃ | Exhibits different optical properties |
| Praseodymium Trifluoride | PrF₃ | Less stable than CeF₃ under certain conditions |
Cerium trifluoride's distinct low solubility and specific reactivity patterns make it particularly valuable in applications requiring moisture resistance and stability under varying conditions .
Crystal Structure
Hexagonal Crystal System
Cerium trifluoride crystallizes in the hexagonal crystal system, adopting the tysonite structure type, which is also known as the lanthanum trifluoride structure [2] [8]. The compound exhibits a three-dimensional framework where cerium ions are arranged in layers situated very close together, while fluorine ions occupy three distinct crystallographic positions within the lattice structure [6] [7]. This hexagonal arrangement is characteristic of rare earth trifluorides and represents the stable phase under ambient conditions [15] [22].
The hexagonal structure of cerium trifluoride has been confirmed through extensive X-ray diffraction analysis, which exhibits characteristic peaks that agree with the hexagonal crystalline arrangement [6]. The crystalline structure can transition between hexagonal at high temperatures and trigonal at lower temperatures, though the hexagonal form is predominantly observed in most experimental conditions [6] [10].
Lattice Parameters and Constants
The lattice parameters of cerium trifluoride have been determined through multiple crystallographic studies, with consistent values reported across different research groups. The hexagonal unit cell is characterized by specific lattice constants that define the three-dimensional arrangement of atoms within the crystal structure.
| Parameter | Value (Å) | Space Group | Source |
|---|---|---|---|
| a | 7.10 | P6₃/mmc | [10] |
| c | 7.31 | P6₃/mmc | [10] |
| a | 7.1408 | P-3c1 | [14] |
| c | 7.297 | P-3c1 | [14] |
| a | 7.1804 | P-3c1 | [14] |
| c | 7.346 | P-3c1 | [14] |
The space group designation varies between P6₃/mmc and P-3c1 depending on the specific crystallographic analysis and temperature conditions [10] [12] [14]. The lattice constants demonstrate slight variations based on synthesis conditions and measurement techniques, with the a-parameter consistently ranging from 7.10 to 7.18 Å and the c-parameter from 7.30 to 7.35 Å [10] [14].
Coordination Geometry
The coordination environment within cerium trifluoride is characterized by cerium ions adopting a nine-coordinate geometry [2] [4] [8]. The cerium cations exhibit an approximately tricapped trigonal prismatic coordination arrangement, though this can be considered eleven-coordinate if two more distant fluoride ions are included in the coordination sphere [2] [8].
The cerium-fluorine bond distances span a range from 2.37 to 2.94 Å, indicating the presence of both shorter and longer coordination bonds within the structure [7]. The Materials Project database reports that cerium ions are bonded in a twelve-coordinate geometry to twelve fluoride atoms, with bond distances ranging from 2.37 to 2.94 Å [7].
The three crystallographically independent fluoride ions exhibit different coordination environments, ranging from three-coordinate with trigonal planar geometry to more complex arrangements [2] [8]. The first fluoride site adopts trigonal planar geometry coordinated to three equivalent cerium atoms, while the second fluoride site exhibits one-coordinate geometry bonded to four equivalent cerium atoms and one fluoride atom [7]. The third fluoride site forms face-sharing fluoride-cerium-fluoride cuboctahedra, bonded to six equivalent cerium atoms and six equivalent fluoride atoms [7].
High-Pressure Structural Behavior
Hexagonal-to-Orthorhombic Phase Transition
Cerium trifluoride undergoes a significant structural phase transition under high-pressure conditions, transforming from its ambient hexagonal phase to an orthorhombic structure [22]. This pressure-induced transformation has been extensively studied using in situ X-ray diffraction measurements and represents a fundamental change in the crystallographic arrangement of the compound [22].
The hexagonal-to-orthorhombic phase transition is characterized by the gradual appearance of new diffraction peaks at approximately 14 degrees two-theta angle, manifesting the beginning of the structural transformation [22]. The transition process is gradual rather than abrupt, with both phases coexisting over a significant pressure range [22].
During the phase transition, the distance between cerium and terbium ions, as well as cerium-cerium distances, exhibits remarkable behavior [22]. In the pressure range from 2.1 to 16.2 gigapascals, these interatomic distances decrease gradually with increasing pressure [22]. However, above 16.2 gigapascals, coinciding with the onset of the phase transition, the distances increase significantly [22].
Critical Pressure Points and Transition Mechanisms
The critical pressure for the initiation of the hexagonal-to-orthorhombic phase transition in cerium trifluoride occurs at approximately 18.9 gigapascals [22]. The transformation process continues progressively until 30.9 gigapascals, indicating an extended pressure range over which the structural reorganization takes place [22].
| Pressure Range (GPa) | Structural Behavior | Phase Composition |
|---|---|---|
| 0-16.2 | Hexagonal phase stable | Single phase hexagonal |
| 16.2-18.9 | Transition onset | Mixed phase region |
| 18.9-30.9 | Active transformation | Hexagonal + Orthorhombic |
| >30.9 | Orthorhombic dominant | Predominantly orthorhombic |
The transition mechanism involves the gradual weakening of hexagonal phase diffraction peaks while orthorhombic phase peaks strengthen with increasing pressure [22]. This behavior indicates a reconstructive phase transformation where the atomic arrangement undergoes significant reorganization rather than a simple distortion of the existing structure [22].
The phase transition is completely reversible upon decompression, with the structure returning to its initial hexagonal phase when pressure is released to ambient conditions [22]. This reversibility demonstrates that the high-pressure orthorhombic phase is metastable and that the hexagonal structure represents the thermodynamically stable configuration under normal conditions [22].
Microstructural Characteristics
Grain Boundaries and Defect Formation
The microstructural characteristics of cerium trifluoride are significantly influenced by the presence of various defects and impurities within the crystal lattice [26] [28]. Crystal growth studies have revealed that the formation of perturbed centers arises primarily from anion vacancies and the presence of oxygen ions in the vicinity of these defects [26].
Oxygen-containing impurities represent the most significant defect type in cerium trifluoride crystals, with concentrations varying dramatically depending on the crystal growth conditions and position within the grown boule [28] [29]. In high-quality crystals grown using the Bridgman method, oxygen contents in the bottom and center parts measure 30-35 parts per million, while the concentration increases substantially to 200 parts per million in the upper milky crystal regions [28] [29].
The segregation of oxygen impurities during directional crystallization results in effective purification of the lower portions of the crystal while concentrating defects in the upper regions [28] [29]. This segregation behavior is attributed to the low isomorphic capacity of the cerium trifluoride structure with respect to oxygen-containing impurities, which are pushed into the melt during the growth process and accumulate in the final solidification zones [28] [29].
Defect formation is also influenced by the presence of monovalent cations such as lithium and sodium, which can create similar segregation effects and contribute to the formation of milky regions in the upper portions of grown crystals [28] [29]. The effective removal of oxide admixtures from source materials during crystallization requires specialized techniques, including the use of active fluorinating atmospheres created through the thermal decomposition of polytetrafluoroethylene [26].
Surface Morphology
The surface morphology of cerium trifluoride crystals varies significantly depending on the synthesis method and growth conditions employed [31]. Microwave-assisted synthesis produces novel flower-like nanostructures with mean diameters of approximately 190 nanometers, characterized by complex three-dimensional arrangements of intercrossed petals [31].
Transmission electron microscopy analysis reveals that these flower-like structures consist of several petals with thickness of approximately 14 nanometers that intercross together and extend toward the edges of the flower-shaped formations [31]. The growth process follows a time-dependent evolution from small nanoparticles to oblate nanodisks with blurry outlines, which subsequently assemble to form the final flower-like morphologies [31].
In single crystal growth applications, the surface characteristics are dominated by crystallographic orientation effects [28] [29]. The cleavage plane (0001) exhibits a characteristic metallic luster, indicating smooth surface termination along this specific crystallographic direction [28] [29]. High-quality crystals grown using the Bridgman method display colorless and transparent characteristics with no light-scattering inclusions observed in the bulk material [28] [29].
Surface analysis of cerium trifluoride demonstrates excellent optical characteristics that approach theoretical values, indicating the absence of significant surface defects that would otherwise contribute to optical losses [29]. The optical transparency limit is determined by the onset of interconfigurational 4f-5d transitions in the cerium ion, which defines the fundamental electronic properties of the material surface [29].
Energy Band Structure
The energy band structure of cerium trifluoride represents a fundamental aspect of its electronic properties, determining the material's optical, electronic, and luminescent characteristics. First-principles calculations using density functional theory have revealed distinctive features in the electronic structure of this compound that distinguish it from other rare-earth fluorides.
Conduction Band Configuration
The conduction band of cerium trifluoride is formed predominantly by the 5d states of cerium three-plus ions [1]. This configuration arises from the unique electronic structure of cerium, where the 5d orbitals participate significantly in the conduction processes. The conduction band exhibits a complex structure that can be understood through careful analysis of the electronic density of states and band dispersion calculations.
The formation of the conduction band through 5d cerium states creates a distinctive electronic environment that influences the material's scintillation properties. The 5d states of cerium three-plus ions dominate the conduction band region, with contributions from other atomic orbitals being minimal and at the level of calculation error [1]. This predominance of cerium 5d states in the conduction band is crucial for understanding the luminescent properties of cerium trifluoride.
| Parameter | Value | Method |
|---|---|---|
| Conduction Band Formation | 5d states of Ce³⁺ | DFT calculations |
| Valence Band Formation | 2pF⁻ states | DFT calculations |
| 4f Band Position | 4.5 eV above valence band | PAW method |
| Energy Gap (4f-5d) | 3 eV | PAW method |
| Energy Gap (theoretical) | 3 eV | PAW method |
| Energy Gap (experimental) | 5 eV | Experimental |
5d1 and 5d2 Subbands
A remarkable feature of the cerium trifluoride conduction band is its separation into two distinct subbands, designated as 5d1 and 5d2, which exhibit significantly different electronic properties [1]. This separation represents a fundamental characteristic of the electronic structure and has profound implications for the material's optical and electronic behavior.
The 5d1 subband, located at the bottom of the conduction band, displays smaller dispersion compared to the 5d2 subband [1]. This reduced dispersion indicates that electrons in the 5d1 subband have limited mobility and tend toward localization. The smaller dispersion of 5d1 states at the bottom of the conduction band at the gamma point, compared with the 5d2 upper band states, provides direct evidence for the distinct nature of these subbands [1].
The 5d2 subband, positioned at higher energies within the conduction band, exhibits greater dispersion and consequently different transport properties. This subband separation has been observed not only in cerium trifluoride but also in other cerium halides, including cerium trichloride and cerium tribromide, suggesting a general phenomenon in cerium-based compounds [1].
| Subband | Effective Mass (me) | Dispersion | Characteristics |
|---|---|---|---|
| 5d1 | 4.9 | Small | Facilitates electron localization |
| 5d2 | 0.9 | Large | Higher mobility |
Effective Electron Masses
The effective electron masses in the two conduction subbands of cerium trifluoride have been determined through careful analysis of the band dispersion relations. Using the quadratic dispersion law around the gamma point and the standard formula for effective mass calculation, distinct values have been obtained for each subband [1].
The effective electron mass in the 5d1 subband is 4.9 times the free electron mass, while the 5d2 subband exhibits an effective mass of 0.9 times the free electron mass [1]. This significant difference in effective masses reflects the contrasting electronic properties of the two subbands and has important consequences for charge carrier dynamics within the material.
The large effective electron mass in the 5d1 subband facilitates the localization of electronic excitations, leading to the formation of Frenkel self-trapped excitons [1]. This localization is fundamental to the luminescent properties of cerium trifluoride and explains the material's effectiveness as a scintillator. The formation of these localized states results from the phonon relaxation of the exciton electronic component, creating stable luminescent centers.
Electronic States of Ce3+ Ions
The electronic states of cerium three-plus ions in the cerium trifluoride crystal lattice play a central role in determining the material's optical and luminescent properties. The interaction between the 4f and 5d electronic states of cerium creates the fundamental electronic transitions responsible for the material's scintillation characteristics.
4f-5d Transitions
The 4f-5d transitions in cerium three-plus ions represent the primary mechanism for optical excitation and luminescence in cerium trifluoride. These transitions occur between the 4f ground state and the 5d excited states, with the transition energies and probabilities determining the material's spectroscopic properties [2] [3].
The transitions between the 4f state and the 5d1 states are characterized as intracenter transitions, meaning they occur within individual cerium ions rather than involving charge transfer between different ions [1]. This intracenter nature leads to the formation of Frenkel excitons, which are localized excited states that can migrate through the crystal lattice while maintaining their bound electron-hole character.
The excitation spectra of cerium trifluoride in the 4-6 electron volt range exhibit structured features due to the splitting of the 5d levels by the crystal field [1]. The luminescence peaked at 290 nanometers corresponds to the radiative decay of these 4f-5d transitions, specifically involving the Frenkel self-trapped excitons formed through the interaction of 4f holes with 5d1 electrons [1].
Multiple absorption bands have been identified in the excitation spectra, with dips observed at 5.01, 5.30, 5.66, 5.97, and 6.45 electron volts [1]. These features correlate with the crystal field splitting of the 5d levels, providing detailed information about the electronic structure and the influence of the crystalline environment on the cerium electronic states.
Influence of Crystal Field on 5d States
The crystal field environment in cerium trifluoride exerts a profound influence on the 5d electronic states of cerium three-plus ions. The crystal structure of cerium trifluoride, which adopts the lanthanum trifluoride or tysonite structure, provides a specific coordination environment that determines the splitting and energetic ordering of the 5d states [4].
In the cerium trifluoride structure, cerium ions adopt a 9-coordinate geometry with an approximately tricapped trigonal prismatic coordination environment [4]. This coordination geometry creates a crystal field that splits the originally degenerate 5d orbitals into multiple energy levels. The strength and symmetry of this crystal field determine the energy differences between the split 5d states and consequently influence the optical transitions.
The crystal field splitting of the 5d states is responsible for the structured appearance of the excitation spectra and determines the specific energies at which optical transitions occur [2]. The low-symmetry crystal field environment leads to significant splitting of the 5d levels, with the energy separations between different 5d components being large enough to be resolved in spectroscopic measurements.
| Property | Value |
|---|---|
| Crystal Structure | Hexagonal (tysonite) |
| Space Group | P-3c1 |
| Coordination Number | 9 |
| Coordination Geometry | Tricapped trigonal prismatic |
| Lattice Parameters | a = 7.10 Å, c = 7.31 Å |
| Density | 6.16 g/cm³ |
The influence of the crystal field extends beyond simple energy level splitting to affect the nature of the electronic wave functions and the transition probabilities between different states. The specific symmetry of the crystal field determines which transitions are allowed and which are forbidden, directly influencing the intensity and polarization characteristics of the observed optical transitions.
Computational Studies of Electronic Structure
Computational studies have provided crucial insights into the electronic structure of cerium trifluoride, complementing and extending experimental observations. These theoretical investigations have employed various levels of approximation and different computational methods to understand the complex electronic behavior of this material.
First-Principle Calculations
First-principles calculations of cerium trifluoride have been performed using density functional theory implemented in various computational packages, including the open-source ABINIT software [1]. These calculations aim to predict the electronic structure, band gaps, and optical properties of the material from fundamental quantum mechanical principles without relying on empirical parameters.
The first-principles approach involves solving the Schrödinger equation for the many-electron system of cerium trifluoride using density functional theory. The calculations include all electrons in the system and treat the electron-electron interactions through exchange-correlation functionals. The computational results provide detailed information about the electronic density of states, band structure, and the energetic positions of different electronic levels.
However, first-principles calculations face significant challenges when applied to cerium trifluoride due to the presence of strongly correlated 4f electrons. The standard density functional theory methods tend to underestimate the energy gaps between different electronic states, with calculated values often being significantly lower than experimental measurements [1]. For cerium trifluoride, the calculated 4f-5d energy gap is approximately 3 electron volts, compared to the experimental value of 5 electron volts [1].
Despite these limitations, first-principles calculations provide valuable information about the relative energetic ordering of different electronic states, the nature of the electronic wave functions, and the trends in electronic properties. The calculations successfully predict the formation of the conduction band from cerium 5d states and the separation into distinct 5d1 and 5d2 subbands [1].
Density Functional Theory Approaches
Standard density functional theory approaches, including the local density approximation and generalized gradient approximation, have been applied to cerium trifluoride with varying degrees of success. These methods are based on the concept of expressing the many-electron ground state energy as a functional of the electron density, thereby reducing the computational complexity of the many-body problem.
The local density approximation and generalized gradient approximation functionals are designed for systems with relatively uniform electron distributions and are based on the model of a homogeneous electron gas [1]. However, these functionals cannot correctly describe the strongly localized 4f states of lanthanide ions with the required accuracy. The 4f electrons in cerium exhibit strong correlation effects that are not adequately captured by these standard exchange-correlation functionals.
The inadequacy of standard density functional theory methods for cerium trifluoride stems from the unique electronic structure of cerium, where the 4f electrons exist in a regime between localized and delocalized behavior. The standard functionals systematically underestimate the energy required to remove 4f electrons and place them in the conduction band, leading to incorrect predictions of the electronic structure and optical properties.
| Method | Advantages | Limitations | Accuracy for CeF3 |
|---|---|---|---|
| Local Density Approximation (LDA) | Computationally efficient | Underestimates band gaps | Poor for 4f states |
| Generalized Gradient Approximation (GGA) | Better than LDA for many systems | Insufficient for f-electrons | Poor for 4f states |
| Projector Augmented Wave (PAW) | All-electron accuracy | Requires more resources | Good structural properties |
| PAW with PBE0 Hybrid Functional | Improved description of localized states | Computationally demanding | Best for electronic structure |
| DFT+U Method | Corrects for strong correlation | Requires U parameter selection | Good for correlated electrons |
PAW Method with Hybrid Exchange-Correlation Functionals
The projector augmented wave method combined with hybrid exchange-correlation functionals represents a significant advancement in the computational treatment of cerium trifluoride. This approach addresses many of the limitations of standard density functional theory methods and provides more accurate descriptions of the electronic structure.
The projector augmented wave method maintains all-electron accuracy while using computationally efficient pseudopotentials [1]. This method reconstructs the full electron wave function in the core region of atoms, providing accurate descriptions of both valence and core electronic states. For cerium trifluoride, this approach correctly describes the interaction between the 4f and 5d states and their hybridization with the fluorine 2p states.
The hybrid exchange-correlation functionals, particularly the PBE0 functional, incorporate a fraction of exact Hartree-Fock exchange with the density functional theory exchange-correlation energy [1]. This mixing of exact exchange helps to correct the self-interaction error that plagues standard density functional theory methods and provides a more accurate description of strongly correlated electrons.
The PBE0 hybrid functional used in cerium trifluoride calculations requires significantly more computational resources than standard density functional theory methods but provides more accurate energy parameters due to the reduced number of approximations [1]. The hybrid functional approach successfully captures the essential physics of the 4f-5d interactions and provides predictions that are in much better agreement with experimental observations.
Physical Description
Hydrogen Bond Acceptor Count
Exact Mass
Monoisotopic Mass
Heavy Atom Count
UNII
GHS Hazard Statements
Reported as not meeting GHS hazard criteria by 9 of 55 companies. For more detailed information, please visit ECHA C&L website;
Of the 4 notification(s) provided by 46 of 55 companies with hazard statement code(s):;
H312 (89.13%): Harmful in contact with skin [Warning Acute toxicity, dermal];
H315 (100%): Causes skin irritation [Warning Skin corrosion/irritation];
H319 (100%): Causes serious eye irritation [Warning Serious eye damage/eye irritation];
H332 (89.13%): Harmful if inhaled [Warning Acute toxicity, inhalation];
H335 (100%): May cause respiratory irritation [Warning Specific target organ toxicity, single exposure;
Respiratory tract irritation];
Information may vary between notifications depending on impurities, additives, and other factors. The percentage value in parenthesis indicates the notified classification ratio from companies that provide hazard codes. Only hazard codes with percentage values above 10% are shown.
Pictograms

Irritant
Other CAS
7758-88-5