Home / Products / Building Blocks / Fluorinated Building Blocks

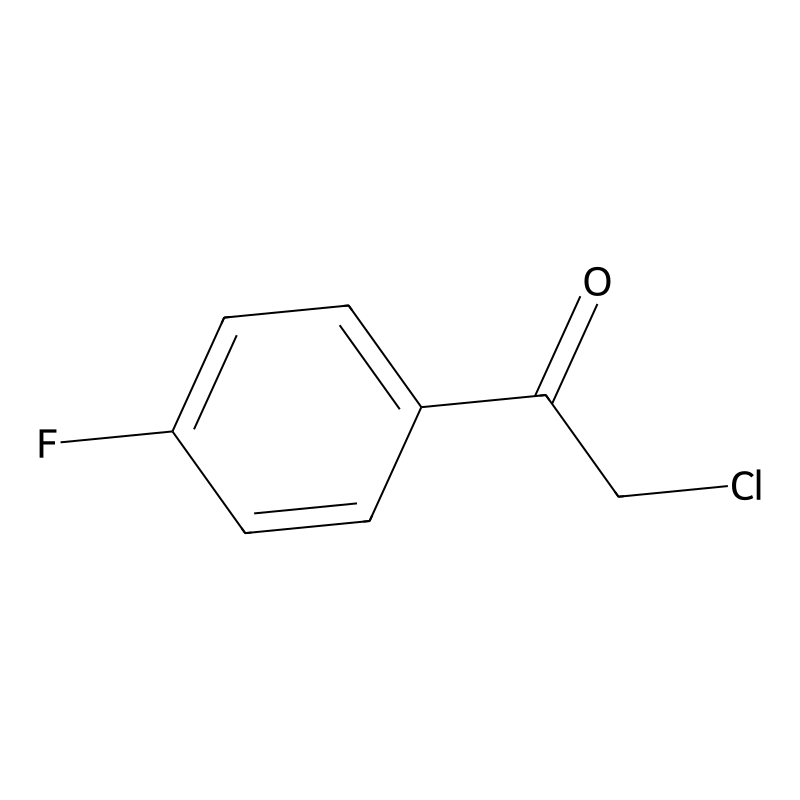
2-Chloro-4'-fluoroacetophenone

Name: 2-Chloro-4'-fluoroacetophenone
Brand: Smolecule
SKU: S603321
Rating: 5 (1 reviews)

Catalog No.

S603321

CAS No.

456-04-2

M.F

C8H6ClFO

M. Wt

172.58 g/mol

Availability

In Stock

* This item is exclusively intended for research purposes and is not designed for human therapeutic applications or veterinary use.

3. Specification
4. Others

General Information

CAS Number

456-04-2

Product Name

2-Chloro-4'-fluoroacetophenone

IUPAC Name

2-chloro-1-(4-fluorophenyl)ethanone

Molecular Formula

C8H6ClFO

Molecular Weight

172.58 g/mol

InChI

InChI=1S/C8H6ClFO/c9-5-8(11)6-1-3-7(10)4-2-6/h1-4H,5H2

InChI Key

UJZWJOQRSMOFMA-UHFFFAOYSA-N

SMILES

C1=CC(=CC=C1C(=O)CCl)F

Synonyms

2-Chloro-1-(4-fluorophenyl)ethanone; 2-Chloro-4’-fluoroccetophenone; 2-Chloro-1-(4-fluorophenyl)-1-ethanone; 2-Chloro-1-(4’-fluorophenyl)ethanone; 2-Chloro-4’-fluoroacetophenone; 2’-Chloro-4-fluoroacetophenone; 4’-Fluoro-2-chloroacetophenone; Chlorom

Canonical SMILES

C1=CC(=CC=C1C(=O)CCl)F

Scientific Research Applications

Synthesis of S-(phenacyl)glutathiones

One application of 2-chloro-4'-fluoroacetophenone is in the synthesis of S-(phenacyl)glutathiones. Glutathione is a tripeptide molecule essential for various biological functions, including detoxification and antioxidant activity. S-(phenacyl)glutathione derivatives are synthetic analogs of glutathione that have been studied for their potential therapeutic applications.

A study published in the journal "Chemical & Pharmaceutical Bulletin" describes the synthesis of several S-(phenacyl)glutathione derivatives, including one derived from 2-chloro-4'-fluoroacetophenone. The researchers found that these derivatives exhibited inhibitory activity against enzymes involved in the biosynthesis of cholesterol, suggesting their potential as antihyperlipidemic agents [1].

[1] "Synthesis and Evaluation of S-(Phenacyl)glutathione Derivatives as Inhibitors of HMG-CoA Reductase and Cholesterol Acyltransferase" by Wei Wang et al., Chemical & Pharmaceutical Bulletin (2005) 53(11): 1452-1456

Specification

XLogP3

2.3

Others

GHS Hazard Statements

Aggregated GHS information provided by 134 companies from 9 notifications to the ECHA C&L Inventory. Each notification may be associated with multiple companies.;
H301 (66.42%): Toxic if swallowed [Danger Acute toxicity, oral];
H314 (70.9%): Causes severe skin burns and eye damage [Danger Skin corrosion/irritation];
H315 (29.85%): Causes skin irritation [Warning Skin corrosion/irritation];
H317 (64.18%): May cause an allergic skin reaction [Warning Sensitization, Skin];
H318 (64.18%): Causes serious eye damage [Danger Serious eye damage/eye irritation];
H319 (29.85%): Causes serious eye irritation [Warning Serious eye damage/eye irritation];
H330 (64.18%): Fatal if inhaled [Danger Acute toxicity, inhalation];
H335 (29.1%): May cause respiratory irritation [Warning Specific target organ toxicity, single exposure;
Respiratory tract irritation];
H410 (64.18%): Very toxic to aquatic life with long lasting effects [Warning Hazardous to the aquatic environment, long-term hazard];
Information may vary between notifications depending on impurities, additives, and other factors. The percentage value in parenthesis indicates the notified classification ratio from companies that provide hazard codes. Only hazard codes with percentage values above 10% are shown.