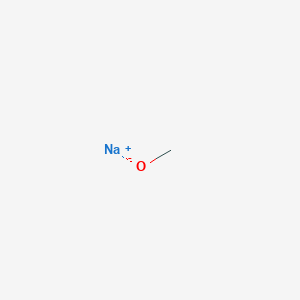
Sodium methanolate

Organic Synthesis:

• Base and Catalyst: Sodium methoxide functions as a strong base and a catalyst in various organic reactions, including Claisen condensations, aldol condensations, and deprotonation steps. Its ability to deprotonate acidic protons facilitates further reactions by generating reactive nucleophiles.
• Nucleophile: The methoxide ion (OCH₃⁻) acts as a nucleophile in reactions like methylation, where it replaces other leaving groups with a methyl group (CH₃). This plays a crucial role in the synthesis of various organic molecules, including pharmaceuticals, agrochemicals, and natural products.

Polymerization:

• Initiator: Sodium methoxide can initiate the anionic polymerization of cyclic ethers like ethylene oxide, leading to the formation of high molecular weight polyethers. These polymers are used in various applications, such as electrolytes in batteries, lubricants, and components in personal care products.

Biodiesel Production:

• Transesterification Catalyst: Sodium methoxide serves as a catalyst in transesterification reactions, which convert triglycerides (fats and oils) into biodiesel fuel. This process involves the reaction of triglycerides with methanol to form fatty acid methyl esters (FAME), the main component of biodiesel.

Other Applications:

• Demethylation: Sodium methoxide can be used for demethylation reactions in specific contexts, such as the removal of methyl protecting groups in organic synthesis.
• Purification: It finds use in the purification of some organic compounds by extracting acidic impurities.

Sodium methoxide is the simplest alkali metal alkoxide, formed by the deprotonation of methanol (CH₃OH) []. It appears as a white, hygroscopic (readily absorbs moisture) powder []. Its significance lies in its strong basic character, making it a valuable reagent for various organic transformations [].

Molecular Structure Analysis

The Lewis structure of sodium methoxide features an ionic bond between sodium (Na⁺) and a methoxide anion (CH₃O⁻). The methoxide anion has a tetrahedral geometry with the carbon atom (C) at the center bonded to three hydrogen atoms (H) and a single oxygen atom (O) with a negative formal charge. The sodium cation loses its single valence electron, resulting in a stable octet configuration for both Na⁺ and CH₃O⁻ [].

Chemical Reactions Analysis

Sodium methoxide participates in various chemical reactions due to its strong basicity and nucleophilicity (attracted to positively charged centers). Here are some key reactions:

• Deprotonation

  Sodium methoxide acts as a base, abstracting a proton (H⁺) from weakly acidic compounds like alcohols (ROH) to generate alkoxide ions (RO⁻) and methane (CH₄). This reaction is crucial for various organic syntheses [].

  CH₃OH + NaCH₃O → CH₃ONa + CH₄ (Eq. 1) []

• Claisen condensation

  This reaction utilizes sodium methoxide as a catalyst to form β-ketoesters (compounds with a carbonyl group next to a ketone or ester) from esters and aldehydes or ketones [].

  RCOOCH₃ + CH₃CHO + NaCH₃O → RCOC(CH₃)=CHCOO⁻Na⁺ + CH₃OH (Eq. 2) []

• Transesterification

  This reaction plays a vital role in biodiesel production. Sodium methoxide acts as a catalyst, converting triglycerides (fats and oils) into fatty acid methyl esters (biodiesel) and glycerol [].

  Triglyceride + 3 CH₃OH → 3 Fatty Acid Methyl Esters + Glycerol (Eq. 3) []

• Williamson ether synthesis

  Sodium methoxide serves as a base for the synthesis of ethers (compounds with an oxygen atom connecting two alkyl groups) from haloalkanes (compounds with a halogen atom bonded to an alkyl group) and alcohols [].

  RX + CH₃OH + NaCH₃O → R-O-CH₃ + NaX (Eq. 4) [] (X represents a halogen)

Physical And Chemical Properties Analysis

• Formula: CH₃ONa
• Molar mass: 54.03 g/mol []
• Melting point: 127 °C []
• Boiling point: Decomposes above 300 °C []
• Solubility: Soluble in methanol, ethanol, and liquid ammonia; insoluble in non-polar solvents like hydrocarbons []
• Stability: Hygroscopic, reacts violently with water and acids []