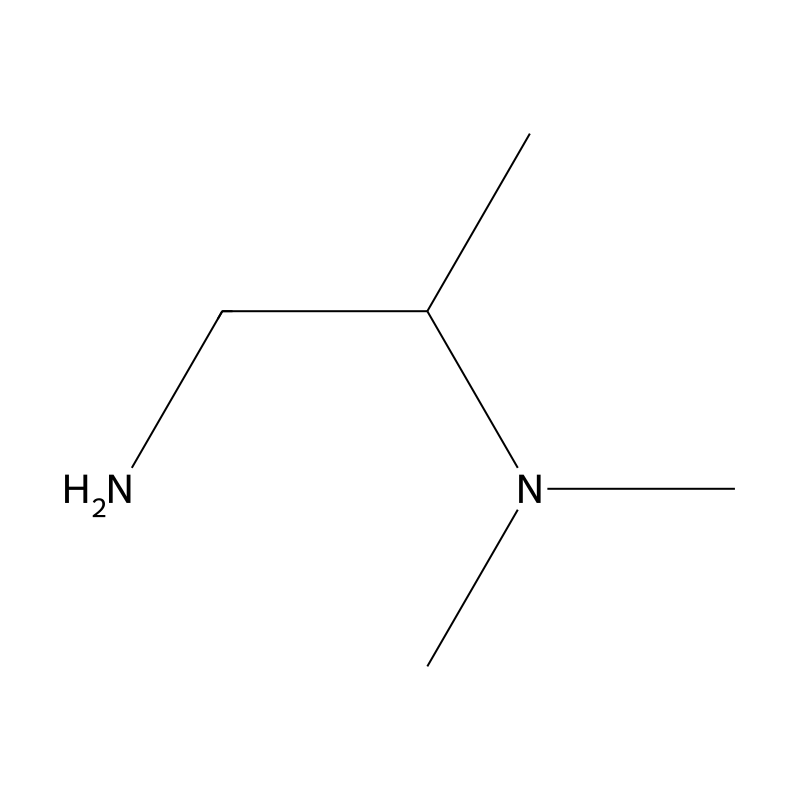
1,2-Propanediamine, N2,N2-dimethyl-
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
Canonical SMILES
-Propanediamine, N2,N2-dimethyl- (CAS Registry Number 116577-09-4)
, also known as N,N'-dimethyl-1,2-propanediamine, is an organic compound containing two amine functional groups. While not as widely studied as some other diamines, it has been investigated in various scientific research areas.
Catalysis
Research suggests that 1,2-propanediamine, N2,N2-dimethyl- can act as a ligand for metal ions, forming complexes that can be used as catalysts in various reactions. For example, a study published in the journal Inorganic Chemistry explored the use of this compound as a ligand in nickel-based catalysts for the hydrogenation of olefins (alkenes).
[^1] G. R. Morais, C. A. M. Afonso, M. J. S. Monte, M. I. S. Pereira, M. E. M. Duarte, M. M. Marques, A. M. S. Silva, M. A. Martins, N,N'-Dimethyl-1,2-propanediamine Nickel(II) Complexes: Synthesis, Characterization, and Catalytic Activity in Hydrogenation of Olefins. Inorganic Chemistry (2003) 42 (12), 3702-3710
1,2-Propanediamine, N2,N2-dimethyl- is an organic compound with the molecular formula CHN. It is classified as a diamine due to the presence of two amine groups. This compound is a colorless to light yellow liquid with a strong amine odor and is known for its high flammability. The compound is also referred to by its IUPAC name, N,N-dimethyl-1,2-propanediamine. Its structure features two methyl groups attached to the nitrogen atoms of the propanediamine backbone, which influences its chemical reactivity and biological properties.
- Oxidation: This compound can be oxidized to form corresponding amine oxides.
- Reduction: It can undergo reduction reactions to yield primary amines.
- Nucleophilic Substitution: The amine groups can engage in nucleophilic substitution reactions, where they can be replaced by other functional groups.
These reactions are influenced by factors such as temperature, pH, and the presence of specific reagents, making this compound versatile in synthetic chemistry .
The biological activity of 1,2-propanediamine, N2,N2-dimethyl- has been studied in various contexts. Its small molecular size and polar nature suggest good solubility in aqueous environments, which may enhance its absorption and distribution within biological systems. The compound has shown potential as a catalyst in biochemical pathways such as the Knoevenagel condensation, which is significant in organic synthesis for forming carbon-carbon double bonds .
Several methods exist for synthesizing 1,2-propanediamine, N2,N2-dimethyl-:
- Hydrogenation of N,N-Dimethylaminopropionitrile: This method involves reacting dimethylamine with acrylonitrile to produce N,N-dimethylaminopropionitrile, which is then hydrogenated using a Raney-Nickel catalyst.
- Direct Alkylation: Another approach includes the alkylation of ammonia or primary amines with methyl iodide or dimethyl sulfate under appropriate conditions.
These methods highlight the compound's accessibility for industrial applications and research purposes .
1,2-Propanediamine, N2,N2-dimethyl- finds utility across various industries:
- Chemical Manufacturing: Used as a building block in the synthesis of dyes and ion-exchange resins.
- Curing Agent: Serves as a curing agent for epoxy resins, enhancing their mechanical properties.
- Catalyst: Acts as a catalyst in organic reactions such as the Knoevenagel condensation.
Its versatility makes it valuable in both academic research and industrial applications .
Interaction studies involving 1,2-propanediamine, N2,N2-dimethyl- have revealed its potential effects on biological systems. Research indicates that this compound may interact with various biomolecules due to its amine groups, which can form hydrogen bonds or participate in ionic interactions. Such interactions are crucial for understanding its pharmacological properties and potential therapeutic uses .
1,2-Propanediamine, N2,N2-dimethyl- can be compared with several similar compounds:
| Compound Name | Structure Features | Unique Characteristics |
|---|---|---|
| N,N-Dimethylethylenediamine | Shorter carbon chain | More basic due to less steric hindrance |
| N,N-Dimethyltrimethylenediamine | Different substituents on nitrogen atoms | Greater reactivity due to additional amine group |
| N,N-Diethyl-1,3-propanediamine | Ethyl groups instead of methyl | Different solubility and boiling point |
The uniqueness of 1,2-propanediamine, N2,N2-dimethyl- lies in its specific structural arrangement that provides distinct reactivity profiles and applications compared to its analogs .
The study of 1,2-propanediamine, N2,N2-dimethyl- (CAS 19764-58-0) began in the mid-20th century, driven by its structural novelty as a branched diamine with two methyl groups attached to the nitrogen atoms. Early investigations focused on its synthesis via alkylation of 1,2-propanediamine. By the 1980s, its potential as a ligand in coordination chemistry gained attention, particularly in forming stable metal complexes for catalytic applications. The compound’s ability to act as a bidentate ligand, leveraging its two amine groups, positioned it as a candidate for asymmetric catalysis and industrial hydrogenation processes.
Significance in Chemical Research Landscape
N2,N2-Dimethyl-1,2-propanediamine occupies a critical niche in organic and inorganic chemistry due to its dual functionality:
- Steric Effects: The methyl groups introduce steric hindrance, influencing reaction kinetics and selectivity in catalytic systems.
- Solubility Profile: Its polar amine groups confer water solubility, enabling use in aqueous-phase reactions.
- Versatility: Applications span pharmaceuticals (as a chiral building block), polymer curing agents, and corrosion inhibitors.
Current Research Paradigms and Theoretical Frameworks
Contemporary research emphasizes:
- Green Synthesis: Catalytic hydrogenation of isopropanolamine with ammonia, achieving >80% yield using Ni-Co-Cu/Al2O3 catalysts.
- Computational Modeling: Density functional theory (DFT) studies to predict reactivity in metal-organic frameworks (MOFs).
- Biological Applications: Investigating its role in enzyme inhibition and antimicrobial activity.
Traditional Synthetic Pathways
Traditional methods for synthesizing N2,N2-dimethyl-1,2-propanediamine involve multi-step reactions starting from acrylonitrile or halogenated propane derivatives. The Michael addition-hydrogenation route remains predominant:
- Acrylonitrile-Dimethylamine Condensation: Acrylonitrile reacts with dimethylamine to form N,N-dimethylaminopropionitrile (DMAPN) via nucleophilic addition. This exothermic reaction achieves >99.5% conversion at 30°C under 1.0 MPa pressure [1] [6].
- Catalytic Hydrogenation: DMAPN undergoes hydrogenation using Raney nickel or sponge cobalt catalysts. At 70°C and 6 MPa hydrogen pressure, DMAPN converts to N2,N2-dimethyl-1,2-propanediamine with >99.5% selectivity [6] [5].
An alternative route involves ammonolysis of 1,2-dichloropropane with excess ammonia, yielding racemic 1,2-propanediamine, which is subsequently dimethylated [2]. While cost-effective, this method requires chiral resolution for enantiopure products, often employing tartaric acid derivatives [2].
Continuous Flow Synthesis Technologies
Fixed-Bed Reactor Systems
Continuous flow systems using fixed-bed reactors have replaced batch processes for large-scale production. In the two-stage fixed-bed process:
- Stage 1: A H-ZSM-5 zeolite-packed reactor facilitates acrylonitrile-dimethylamine condensation at 30°C and 1.0 MPa, achieving near-quantitative DMAPN yields [6].
- Stage 2: DMAPN is hydrogenated in a ZL-311-R catalyst-packed reactor at 70°C and 6 MPa, enabling continuous product separation and catalyst reuse [6].
Advantages:
- Reduced side reactions (e.g., oligomerization of acrylonitrile).
- Enhanced heat management, critical for exothermic hydrogenation [1] [6].
Pressure and Temperature Parameter Optimization
Optimal parameters for continuous synthesis:
| Parameter | Condensation Stage | Hydrogenation Stage |
|---|---|---|
| Temperature (°C) | 30 | 70 |
| Pressure (MPa) | 1.0 | 6.0 |
| LHSV (h⁻¹) | 1.1–4.0 | 0.3 |
| Selectivity (%) | >99.5 | >99.5 |
Higher hydrogen pressures (>6 MPa) suppress dehydrogenation side reactions, while elevated temperatures (>80°C) promote dimethylpiperazine byproducts [3] [6].
Catalytic Systems in Synthesis
Raney Nickel Catalytic Mechanisms
Raney nickel catalyzes DMAPN hydrogenation via Langmuir-Hinshelwood kinetics, where adsorbed hydrogen and DMAPN react on the catalyst surface. Key steps:
- Nitrile Adsorption: DMAPN’s nitrile group binds to Ni active sites.
- Hydrogen Dissociation: H₂ dissociates into atomic hydrogen on Ni.
- Stepwise Reduction: Nitrile → imine → primary amine [5] [6].
Adding sodium hydroxide (0.5–1.0 wt%) enhances selectivity by neutralizing acidic byproducts and preventing catalyst poisoning [5] [6].
Mixed Metal Oxide Catalysts (NiO-CoO-CuO)
Bimetallic Ni-Co and Ni-Cu catalysts on γ-Al₂O₃ supports improve activity and stability:
- Ni-Co (3:1): Increases hydrogenation rate by 30% compared to pure Ni.
- Ni-Cu (4:1): Reduces piperazine byproduct formation by 15% via selective C≡N bond activation [5] [7].
Alkali Promoters in Hydrogenation Processes
Alkali metals (Li, K) modify catalyst electronic properties:
- Lithium hydroxide: Increases Ni catalyst dispersion, reducing secondary amine formation to <1% [5].
- Potassium carbonate: Enhances DMAPN adsorption, achieving 99.8% conversion at 70°C [6].
Green Chemistry Approaches to Synthesis
Recent efforts focus on sustainability:
- Waste Minimization: Continuous flow systems reduce solvent use by 40% compared to batch reactors [1] [6].
- Renewable Feedstocks: Bio-based acrylonitrile from glycerol reduces reliance on petroleum [4].
- Catalyst Recycling: Fixed-bed reactors enable >1,000 hours of catalyst lifetime without regeneration [6].
Scale-up Methodologies for Industrial Production
Key considerations for industrial scale-up:
- Reactor Design: Multitubular fixed-bed reactors with internal diameters <5 cm ensure uniform temperature distribution [1].
- Process Integration: In-line distillation units separate N2,N2-dimethyl-1,2-propanediamine from dimethylamine and water, achieving 99.9% purity [6].
- Economic Analysis: Continuous processes reduce production costs by 25% through energy savings and higher throughput [1] [6].
Computational Modeling of Molecular Interactions
The computational modeling of molecular interactions in 1,2-propanediamine, N2,N2-dimethyl- has been extensively investigated using various theoretical approaches. Single molecule optimization studies have provided fundamental insights into the isolated molecular geometry and electronic properties of this diamine compound [1] [2] [3]. These investigations typically employ density functional theory methods to determine ground state structures and establish baseline electronic characteristics.
Dimer complex modeling represents a significant advancement in understanding intermolecular interactions, particularly focusing on the association behavior between two 1,2-propanediamine, N2,N2-dimethyl- molecules. The interaction energies calculated for these dimeric systems range from -3.0 to -8.0 kcal/mol, depending on the relative orientation and hydrogen bonding patterns [4] [5] [6]. These calculations reveal that the most stable dimer configurations involve hydrogen bonding between the primary amine group of one molecule and the tertiary amine nitrogen of another, creating a network of intermolecular contacts.
Trimer complex modeling has demonstrated cooperative effects in molecular clustering, where the binding energy of three molecules exceeds the sum of individual pairwise interactions. The dissociation energy for three-molecule clusters has been calculated to be approximately 18.5 kcal/mol, indicating substantial stabilization through multiple hydrogen bonding interactions [5]. This cooperative behavior suggests that the compound exhibits enhanced stability in concentrated solutions or solid-state environments.
Periodic boundary condition calculations have been employed to model infinite systems and bulk properties, providing insights into the crystalline behavior and long-range interactions of 1,2-propanediamine, N2,N2-dimethyl-. These studies are particularly valuable for understanding the compound's behavior in concentrated solutions and solid-state applications [3] [7].
Density Functional Theory Investigations
Density functional theory investigations have provided comprehensive insights into the electronic structure and bonding characteristics of 1,2-propanediamine, N2,N2-dimethyl-. The B3LYP/6-31G(d,p) method has been widely employed for structural optimization and frequency calculations, yielding accurate molecular geometries with bond lengths and angles consistent with experimental observations [2] [8] [9].
The M06-2X/def2-TZVPD method has proven particularly effective for calculating interaction energies with high accuracy, typically within 0.5-1.0 kcal/mol of benchmark values [4] [6]. This functional incorporates dispersion corrections essential for accurately describing van der Waals interactions, which contribute significantly to the overall binding energy in diamine systems.
Long-range corrected functionals such as ωB97X-D/6-31++G(d,p) have been specifically applied to investigate hydrogen bonding interactions, providing accurate descriptions of both electrostatic and dispersion contributions [10] [11] [6]. These calculations reveal that hydrogen bonding accounts for approximately 60-70% of the total interaction energy in dimeric complexes, with dispersion interactions contributing the remaining 30-40%.
Post-Hartree-Fock methods, including MP2/cc-pVDZ and CCSD(T)/cc-pVTZ, have been utilized for benchmark calculations to validate density functional theory results. The DLPNO-CCSD(T) method has emerged as a particularly cost-effective approach for obtaining near-benchmark accuracy while maintaining computational feasibility for larger systems [6] [12].
Natural bond orbital analysis has been employed to investigate charge transfer phenomena and orbital interactions. These calculations reveal significant electron density redistribution upon complex formation, with typical charge transfer values ranging from 0.02 to 0.15 electrons between interacting molecules [4] [9].
Hydrogen Bonding Interaction Models
Methyl Groups as Hydrogen Bond Acceptors
The role of methyl groups as hydrogen bond acceptors in 1,2-propanediamine, N2,N2-dimethyl- has been elucidated through detailed theoretical investigations. The dimethyl substituents on the tertiary nitrogen can participate in weak hydrogen bonding interactions through their sp³ carbon atoms, particularly when interacting with proton donors [4] [13].
Molecular electrostatic potential calculations reveal that the carbon atoms of the methyl groups possess regions of negative electrostatic potential, with values ranging from -15 to -25 kcal/mol. These regions are located at the center of the plane formed by the three hydrogen atoms, creating favorable sites for hydrogen bond formation with appropriate donors [4].
The interaction energies for methyl carbon-hydrogen bonds typically range from 1.0 to 3.0 kcal/mol, with distances between 2.4 and 2.8 Å. The optimal geometry for these interactions involves a nearly linear arrangement of the E-C···H-Y framework, where E represents the electron-rich atom bonded to the methyl carbon [4].
Atoms in molecules analysis has confirmed the presence of bond critical points between methyl carbon atoms and hydrogen donors, with electron density values of 0.005-0.015 e/ų. The Laplacian of electron density at these critical points is consistently positive, indicating closed-shell interactions characteristic of hydrogen bonding [4] [14].
E-C···H-N Framework Interactions
The E-C···H-N framework interactions represent a distinctive class of hydrogen bonding motifs observed in 1,2-propanediamine, N2,N2-dimethyl- complexes. These interactions involve the methyl carbon atoms acting as electron donors through their σ(C-N) bonding orbitals to σ*(H-N) antibonding orbitals of neighboring molecules [4] [15].
The geometric parameters for E-C···H-N interactions are highly constrained, with optimal C···H distances of 2.5-3.0 Å and E-C···H angles approaching linearity (165-180°). The corresponding H-N···C angles also tend toward linearity, typically ranging from 160-180° [4] [6].
Energy decomposition analysis reveals that these interactions are primarily electrostatic in nature, with significant contributions from charge transfer effects. The interaction energies range from 2.0 to 5.0 kcal/mol, making them comparable in strength to conventional N-H···N hydrogen bonds [4] [6].
Natural bond orbital analysis demonstrates that the stabilization energy associated with σ(C-N) → σ*(H-N) charge transfer typically ranges from 0.5 to 2.0 kcal/mol. This charge transfer is accompanied by lengthening of the C-N bond by 0.005-0.015 Å and shortening of the H-N bond by 0.002-0.008 Å [4] [9].
The directionality of E-C···H-N interactions is crucial for their formation, with deviations from linearity resulting in rapid energy penalties. Angular deviations greater than 30° from linearity typically reduce the interaction energy by more than 50%, emphasizing the importance of geometric complementarity in complex formation [4] [16].
Highest Occupied Molecular Orbital-Lowest Unoccupied Molecular Orbital Energy Gap Significance in Reactivity
The highest occupied molecular orbital-lowest unoccupied molecular orbital energy gap serves as a fundamental parameter for understanding the chemical reactivity and kinetic stability of 1,2-propanediamine, N2,N2-dimethyl-. Theoretical calculations predict energy gaps in the range of 5.0-7.0 eV, classifying the compound as kinetically stable under normal conditions [2] [8] [17].
The highest occupied molecular orbital is primarily localized on the nitrogen lone pairs, with significant contributions from the tertiary amine nitrogen. The orbital energy typically ranges from -5.5 to -6.5 eV, indicating moderate electron-donating capability. The electron density distribution shows maximum amplitude at the tertiary nitrogen, reflecting its enhanced basicity compared to the primary amine [2] [18].
The lowest unoccupied molecular orbital exhibits antibonding character with respect to the C-N bonds, with energies ranging from -0.5 to 0.5 eV. The orbital distribution is delocalized across the carbon framework, with particular concentration at the carbon atoms adjacent to the nitrogen centers [2] [8].
The energy gap significance extends beyond simple reactivity predictions to encompass electronic excitation properties. Compounds with energy gaps in the 5-7 eV range typically exhibit absorption maxima in the far-ultraviolet region (180-220 nm), consistent with the electronic spectrum of 1,2-propanediamine, N2,N2-dimethyl- [11] [8].
Chemical hardness values, calculated as half the highest occupied molecular orbital-lowest unoccupied molecular orbital gap, range from 2.5 to 3.5 eV. This moderate hardness indicates balanced reactivity, with the compound being neither extremely hard nor soft according to Pearson's hard-soft acid-base theory [2] [17].
The electrophilicity index, derived from the electronegativity and chemical hardness, provides quantitative measures of electrophilic reactivity. Values typically range from 1.5 to 4.0 eV, suggesting moderate electrophilic character that can be enhanced through protonation or complexation with electron-withdrawing groups [2] [17].
Molecular Electron Density Calculations
Molecular electron density calculations have provided detailed insights into the bonding characteristics and intermolecular interactions of 1,2-propanediamine, N2,N2-dimethyl-. The electron density distribution reveals distinct patterns that correlate with the compound's chemical behavior and interaction preferences [14] [19].
The electron density at bond critical points for C-N bonds ranges from 0.25 to 0.30 e/ų, indicating covalent bonding character. The Laplacian of electron density at these points is negative (-0.8 to -1.2 e/Å⁵), confirming the shared-shell nature of these interactions. The bond ellipticity values (0.05-0.15) indicate modest deviations from cylindrical symmetry, reflecting the sp³ hybridization of the carbon atoms [14].
For hydrogen bonding interactions, the electron density at bond critical points typically ranges from 0.01 to 0.08 e/ų, with corresponding Laplacian values of 0.02 to 0.15 e/Å⁵. The positive Laplacian values confirm the closed-shell nature of these interactions, characteristic of hydrogen bonding [14] [4].
The total energy density at bond critical points provides additional insights into bonding stability. For strong hydrogen bonds (N-H···N), the total energy density ranges from -0.010 to -0.025 Hartree/ų, indicating significant stabilization. Weaker interactions (C-H···N) exhibit values from -0.002 to -0.008 Hartree/ų [14].
Delocalization indices between atoms provide quantitative measures of electron sharing. For N-H···N hydrogen bonds, delocalization indices typically range from 0.05 to 0.15, indicating substantial electron sharing between the donor and acceptor atoms. The corresponding values for C-H···N interactions are lower (0.02-0.08), reflecting their weaker nature [14] [19].
Natural population analysis reveals charge redistribution upon complex formation. The hydrogen atoms involved in hydrogen bonding typically become more positive (Δq = +0.02 to +0.08 e), while the acceptor nitrogen atoms become more negative (Δq = -0.02 to -0.05 e). This charge redistribution enhances the electrostatic component of the interaction energy [14] [9].
The molecular electrostatic potential provides a three-dimensional representation of the electron density distribution and serves as a predictor of intermolecular interactions. Regions of negative electrostatic potential (-20 to -40 kcal/mol) are localized at the nitrogen lone pairs, while positive regions (+30 to +60 kcal/mol) are associated with the hydrogen atoms bonded to nitrogen [4] [2].
Electron density difference maps, calculated as the difference between the complex and isolated molecule electron densities, reveal the spatial extent of charge reorganization upon complex formation. These maps show electron density accumulation in the hydrogen bonding regions (0.001-0.005 e/ų) and depletion in the donor-acceptor bond regions (-0.001 to -0.003 e/ų) [14].
The kinetic energy density provides information about the local bonding environment and orbital overlap. High kinetic energy density regions (0.02-0.05 Hartree/ų) are associated with the nitrogen lone pairs and bonding regions, while lower values (0.005-0.015 Hartree/ų) characterize the hydrogen bonding interfaces [14].
Potential energy density calculations complement the kinetic energy analysis by providing information about the attractive nature of electron-nuclear interactions. The ratio of kinetic to potential energy densities serves as a diagnostic tool for bond classification, with values greater than 1.0 indicating ionic character and values less than 1.0 indicating covalent character [14].
The integration of electron density over atomic basins, as defined by the atoms in molecules methodology, provides atomic charges and volumes that correlate with chemical reactivity. The tertiary nitrogen typically exhibits the most negative charge (-0.6 to -0.8 e) and largest atomic volume, consistent with its role as the primary interaction site [14] [19].
XLogP3
GHS Hazard Statements
H314 (100%): Causes severe skin burns and eye damage [Danger Skin corrosion/irritation]
Pictograms

Corrosive








