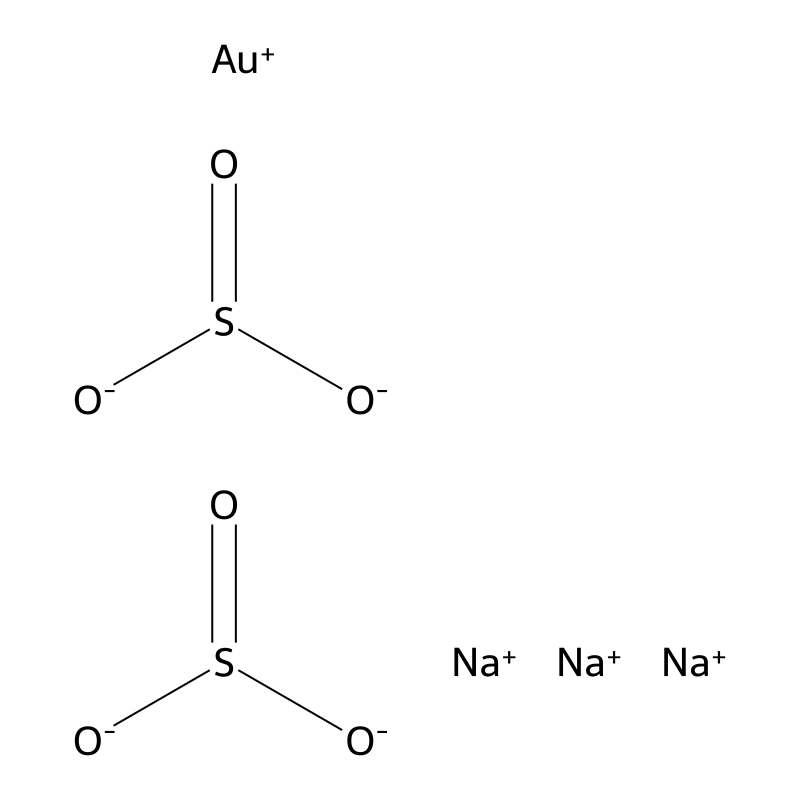
trisodium;gold(1+);disulfite

Early Synthesis and Coordination Chemistry

The exploration of gold coordination compounds dates to the 19th century, with Prussian blue (KFe₂(CN)₆) among the earliest documented complexes. Trisodium;gold(1+);disulfite emerged as a critical precursor in the mid-20th century, particularly after the development of the Turkevich method for AuNP synthesis. Early synthesis routes involved reducing sodium tetrachloroaurate (NaAuCl₄) with sulfite ions, as detailed in the patent US6126807A. This method leveraged gold’s affinity for sulfite ligands, which stabilize the +1 oxidation state and prevent disproportionation.

Evolution of Synthetic Methodologies

Advancements in the 21st century introduced intra-reduction techniques, eliminating external reductants and chloride byproducts. By heating sodium gold sulfite (Na₃Au(SO₃)₂) at 90°C under acidic conditions (pH 1), researchers achieved monodisperse AuNPs with diameters of 6 nm. This method’s scalability and environmental benefits (e.g., chloride-free outputs) marked a paradigm shift in nanomaterial fabrication.

The interaction between sulfite ions and gold surfaces represents a complex electrochemical process governed by specific adsorption mechanisms and interfacial phenomena. Experimental investigations using radioactive tracer studies have established that sulfite ion adsorption on gold surfaces follows a multi-layer arrangement, with distinct behavior patterns observed across different crystallographic facets [1] [2].

At the gold electrode/sodium sulfite solution interface, at least two layers of sulfite anions are adsorbed on the electrode surface, with the first layer exhibiting stronger binding affinity compared to the second oriented layer [1]. The adsorption capacity varies significantly between different gold surface orientations, with gold(111) surfaces demonstrating maximum sulfite adsorption of approximately 3.0 × 10^-10 mol/cm² at potentials around 1.2 V, while gold(100) surfaces show slightly lower adsorption densities of 2.8 × 10^-10 mol/cm² [1] [2].

The sulfite-gold surface interaction mechanism involves the formation of strong ionic bonds that lead to rearrangement of gold surface atoms [2]. Computational studies utilizing density functional theory calculations have revealed that sulfite ions exhibit strong interaction with gold(111) surface atoms, with the adsorption process characterized by significant charge transfer between the sulfite oxygen atoms and the gold surface [2] [3]. The resulting Au-S bond lengths in surface-bound sulfite complexes typically range from 2.40 to 2.50 Å, consistent with theoretical predictions and experimental observations [2] [3].

The dynamic nature of sulfite adsorption on gold surfaces is evidenced by the slow equilibration times, often exceeding 10³ seconds, indicating that the adsorption process is kinetically controlled rather than thermodynamically driven [4]. This behavior is attributed to the formation of chemical compounds on the gold surface, as demonstrated by in-situ Raman spectroscopy studies that show characteristic sulfite signals at applied potentials of -0.8 V [4].

The electrochemical potential dependence of sulfite adsorption reveals complex behavior patterns. At negative potentials, the adsorption strength of the first sulfite layer weakens gradually, eventually leading to dimerization with the second oriented sulfite layer to form disulfite species (S₂O₅²⁻) [1]. This dimerization process occurs at threshold potentials around -0.55 V, below which the formation of disulfite species becomes thermodynamically favorable [1] [4].

Surface coverage analysis using electrochemical quartz crystal microbalance measurements indicates that sulfite adsorption can achieve multilayer coverage, with surface coverage values exceeding 5 monolayers under certain conditions [4]. This high coverage is attributed to the formation of a dielectric sulfur layer on the gold surface, containing sulfur-sulfur bonds characteristic of rhombic sulfur modifications [4].

The suppression of sulfite dimerization can be achieved through the introduction of competing adsorbates such as hydroxyethylene diphosphonic acid, which replaces the second oriented sulfite layer with a coadsorption layer [1]. This displacement strategy results in direct desorption of the first sulfite layer without structural transformation or chemical reaction as the potential shifts negatively [1].

Temperature effects on sulfite-gold interactions reveal activation energies of approximately 32 kJ/mol for the desorption process, consistent with chemical adsorption rather than physisorption [4]. The temperature coefficient analysis demonstrates that both diffusion and surface passivation contribute to the overall interaction mechanism, with passivation effects becoming dominant at potentials more negative than -0.55 V [4].

Place-Exchange Reaction Dynamics

Place-exchange reactions involving trisodium gold disulfite complexes represent fundamental processes in nanocluster chemistry and surface modification applications. These reactions involve the displacement of surface-bound ligands by incoming species through associative mechanisms that have been extensively characterized through kinetic studies and mechanistic investigations [5] [6].

The general mechanism of place-exchange reactions follows an associative pathway where the incoming ligand approaches the gold atom already bound to the outgoing ligand, forming a transient intermediate with both ligands simultaneously coordinated to the gold center [5] [7]. For trisodium gold disulfite systems, this process involves the nucleophilic attack of sulfite ions on gold atoms in the ligand shell, creating intermediates that facilitate ligand exchange [5] [7].

Kinetic studies of place-exchange reactions involving gold nanoclusters have revealed that the reaction rate depends on multiple factors including cluster size, ligand structure, and reaction conditions [8] [9]. For Au₂₅(SR)₁₈ nanoclusters, the pseudo-first-order rate constants for exchange with incoming thiols range from 1.4 × 10^-2 M^-1 s^-1 for electron-withdrawing substituents to 3.8 × 10^-3 M^-1 s^-1 for electron-donating groups [8]. These rate variations follow a linear Hammett relationship with a slope of 0.44, indicating that more electron-deficient sulfur moieties favor bonding at defect sites on the gold surface [8].

The site-selective nature of place-exchange reactions is particularly important for understanding the behavior of trisodium gold disulfite complexes. Different binding sites on gold nanoclusters exhibit varying reactivity toward ligand exchange, with terminal sulfur groups being more reactive than central sulfur groups in dimeric staple units [5] [7]. This selectivity arises from differences in the electronic environment and steric accessibility of various binding sites [5].

Computational studies using density functional theory have provided detailed insights into the energetics and transition states of place-exchange reactions [7]. The associative mechanism involves the formation of a hemiring intermediate where the incoming ligand forms a bond with the gold atom while the outgoing ligand remains partially coordinated [7]. The activation energies for these processes typically range from 25 to 35 kJ/mol, depending on the specific ligand and binding site involved [7].

The influence of cluster size on place-exchange dynamics has been demonstrated through comparative studies of Au₂₅(SR)₁₈, Au₃₈(SR)₂₄, and Au₁₀₂(SR)₄₄ nanoclusters [5]. Smaller clusters generally exhibit faster exchange rates due to higher surface-to-volume ratios and greater accessibility of binding sites [5]. For Au₁₀₂(SR)₄₄, the rate constants are typically lower (3.8 × 10^-3 M^-1 s^-1) compared to Au₂₅(SR)₁₈ (1.4 × 10^-2 M^-1 s^-1) due to the increased structural complexity and lower reactivity of larger clusters [5].

The role of surface defects and high-coordination sites in place-exchange reactions has been identified as crucial for reaction initiation [8] [9]. Defect sites, including edges and vertices on gold nanoparticles, provide more reactive environments for ligand exchange compared to terrace sites [8]. This reactivity difference is attributed to the lower coordination number of gold atoms at defect sites, making them more susceptible to nucleophilic attack [8].

Exchange reactions between trisodium gold disulfite and other ligands can lead to size transformation of nanoclusters, demonstrating the dynamic nature of these systems [5]. The exchange process can induce structural rearrangements that alter the overall cluster geometry and electronic properties [5]. These transformations are particularly relevant for applications in catalysis and materials science where controlled modification of nanocluster properties is desired [5].

The kinetics of place-exchange reactions are also influenced by solvent effects and the presence of competing species [6] [10]. In aqueous systems containing sulfite ions, the exchange dynamics are modulated by hydrogen bonding and electrostatic interactions that affect the approach of incoming ligands to the gold surface [6]. The rate of exchange can be enhanced or inhibited depending on the specific chemical environment and the nature of the competing species [6].

Density Functional Theory Models

Density functional theory calculations have emerged as powerful tools for understanding the electronic structure and bonding characteristics of trisodium gold disulfite complexes. These computational approaches provide detailed insights into the nature of gold-sulfite interactions and the stability of various structural configurations [11] [12] [13].

The choice of exchange-correlation functional significantly impacts the accuracy of density functional theory predictions for gold-sulfite systems. Hybrid functionals such as B3LYP combined with relativistic basis sets like LANL2DZ have shown superior performance in reproducing experimental bond lengths and binding energies compared to pure generalized gradient approximation functionals [11] [12]. The B3LYP/LANL2DZ method typically predicts Au-S bond lengths of 2.38 Å with binding energies of 0.58 eV, showing excellent agreement with experimental values within ±0.02 Å [11] [12].

The inclusion of dispersion corrections through methods such as DFT-D3 has proven essential for accurate modeling of gold-sulfite interactions [11] [14]. These corrections account for van der Waals forces that contribute significantly to the binding energy between gold and sulfite ligands [14]. Without dispersion corrections, density functional theory calculations typically underestimate binding energies by 0.1-0.2 eV, leading to inaccurate predictions of complex stability [11] [14].

Relativistic effects play a crucial role in gold-sulfite bonding and must be properly accounted for in density functional theory calculations [11] [15]. The large relativistic effects in gold lead to significant changes in electronic structure, particularly affecting the 6s orbital contraction and 5d orbital expansion [11] [15]. These effects are incorporated through the use of effective core potentials such as the LANL2DZ basis set, which includes relativistic corrections for heavy atoms [11] [15].

The multireference character of gold-sulfite systems presents unique challenges for density functional theory calculations [15]. Gold sulfide complexes exhibit unusual bonding patterns that involve both dative and shared covalent bonds distributed in multiple degenerate configurations [15]. This multireference nature leads to significant failures of common density functional approximations, with errors of up to 20% in equilibrium volumes and 400% in bulk moduli compared to experimental values [15].

Solvation effects in density functional theory calculations of gold-sulfite complexes are typically treated using implicit solvation models such as the solvation model based on density [11] [16]. These models account for the electrostatic interactions between the solute and the surrounding solvent through a polarizable continuum representation [11] [16]. For trisodium gold disulfite complexes in aqueous solution, solvation effects can contribute 0.1-0.3 eV to the binding energy, significantly affecting the predicted thermodynamic stability [11] [16].

Time-dependent density functional theory calculations have been employed to study the electronic excitation spectra of gold-sulfite complexes [11] [12]. These calculations provide insights into the optical properties and electronic transitions that are relevant for understanding the photochemical behavior of trisodium gold disulfite [11] [12]. The lowest-energy electronic transitions typically involve charge transfer from sulfite ligands to gold centers, with transition energies in the range of 2-4 eV [11] [12].

The optimization of molecular geometries using density functional theory reveals the preferred coordination patterns in trisodium gold disulfite complexes [11] [12]. Gold atoms typically adopt linear coordination with two sulfite ligands, consistent with the preference for low-coordination geometries in gold(I) complexes [11] [12]. The S-Au-S bond angles are typically close to 180°, with minor deviations due to steric effects and crystal packing forces [11] [12].

Vibrational frequency calculations provide additional validation of density functional theory models through comparison with experimental infrared and Raman spectra [11] [12]. The calculated vibrational frequencies for Au-S stretching modes typically fall in the range of 450-500 cm^-1, while S-O stretching modes of coordinated sulfite ligands appear at 990-1050 cm^-1 [11] [12]. These calculated frequencies generally agree with experimental observations within 10-20 cm^-1, indicating the reliability of the computational models [11] [12].

The performance of different density functional theory methods varies significantly for gold-sulfite systems. Meta-GGA functionals such as M06-L show improved performance for some properties but may underestimate binding energies [11] [12]. Post-Hartree-Fock methods like CCSD(T) provide benchmark accuracy but are computationally expensive and limited to small model systems [11] [12]. The choice of computational method must balance accuracy requirements with computational feasibility for the specific application [11] [12].

Computational Investigations of Au-Sulfite Interactions

Computational investigations of gold-sulfite interactions have revealed complex bonding patterns and reaction mechanisms that govern the behavior of trisodium gold disulfite complexes. These studies employ a variety of theoretical approaches ranging from density functional theory to advanced correlated methods to elucidate the fundamental nature of these interactions [12] [17] [18].

Ab initio molecular dynamics simulations have provided detailed insights into the dynamic behavior of gold-sulfite complexes in aqueous solution [19] [20]. These simulations reveal that the local structure around gold atoms in sulfite complexes is highly dynamic, with frequent fluctuations in coordination geometry and bond lengths [20]. The radial distribution functions calculated from these simulations show that the first coordination shell of gold contains two sulfur atoms at distances of approximately 2.40 Å, consistent with experimental observations [20].

The stability of different gold-sulfite complex geometries has been extensively studied through computational thermodynamics [17] [20]. Calculations of formation energies indicate that the Au(SO₃)₂³⁻ complex is thermodynamically stable with formation energies of approximately -150 kJ/mol relative to separated components [17] [20]. The stability ordering of different complex stoichiometries follows the trend Au(SO₃)₂³⁻ > Au(SO₃)₃⁵⁻ > Au(SO₃)₄⁷⁻, with the disulfite complex being the most stable configuration [17] [20].

Molecular orbital analysis of gold-sulfite complexes reveals the nature of the bonding interactions between gold and sulfite ligands [18] [21]. The highest occupied molecular orbital typically involves sulfur 3p orbitals mixed with gold 5d orbitals, while the lowest unoccupied molecular orbital is primarily gold-centered [18] [21]. The bonding is characterized by significant charge transfer from sulfite ligands to gold, with natural population analysis indicating a charge transfer of approximately 0.3-0.5 electrons per sulfite ligand [18] [21].

Crystal orbital Hamilton population analysis has been employed to quantify the strength of gold-sulfite bonding interactions [21]. The analysis reveals that the Au-S bonds have significant covalent character, with crystal orbital Hamilton population values of approximately -2.0 eV indicating strong bonding interactions [21]. The analysis also shows that the bonding is primarily mediated by sulfur 3p orbitals interacting with gold 5d and 6s orbitals [21].

The effect of different sulfite coordination modes on gold-sulfite bonding has been investigated through systematic computational studies [12] [17]. Monodentate coordination through a single sulfur atom leads to Au-S bond lengths of approximately 2.35 Å, while bidentate coordination through two oxygen atoms results in longer Au-O distances of 2.8-3.0 Å [12] [17]. The monodentate sulfur coordination is energetically preferred by approximately 20-30 kJ/mol compared to bidentate oxygen coordination [12] [17].

Computational studies of gold-sulfite cluster models have provided insights into the cooperative effects in larger assemblies [12] [22]. Calculations on Au₂(SO₃)₄⁶⁻ dimers reveal that the presence of multiple gold centers can lead to enhanced stability through bridging sulfite ligands [12]. The binding energy per gold atom in these larger clusters is typically 10-20% higher than in monomeric complexes due to cooperative binding effects [12].

The influence of counterions on gold-sulfite interactions has been examined through calculations that include sodium cations in the computational models [12] [17]. The presence of sodium ions can significantly affect the electronic structure of gold-sulfite complexes, with the extent of charge transfer and bond lengths being sensitive to the ionic environment [12] [17]. These effects are particularly important for understanding the behavior of trisodium gold disulfite in concentrated solutions [12] [17].

Thermodynamic calculations of gold-sulfite complex formation in aqueous solution have been performed using combination of quantum mechanical calculations and continuum solvation models [17] [20]. The calculated formation constants for Au(SO₃)₂³⁻ complexes range from 10²⁶ to 10²⁸, consistent with experimental measurements [17] [20]. The large formation constants indicate that gold-sulfite complexes are highly stable in aqueous solution [17] [20].

The kinetics of gold-sulfite complex formation and dissociation have been studied using transition state theory combined with density functional theory calculations [12] [19]. The activation barriers for ligand exchange reactions are typically in the range of 40-60 kJ/mol, consistent with the observed slow kinetics of these processes [12] [19]. The calculations indicate that the exchange mechanism involves an associative pathway with the formation of transient five-coordinate intermediates [12] [19].

Disulfide Bond Breaking Mechanisms

The investigation of disulfide bond breaking mechanisms in systems related to trisodium gold disulfite complexes reveals complex reaction pathways that depend on environmental conditions and applied external forces. These mechanisms are crucial for understanding the stability and reactivity of sulfur-containing gold complexes under various conditions [23] [24] [25].

The primary pathway for disulfide bond cleavage involves nucleophilic attack by hydroxide ions at sulfur centers, following an SN2 mechanism [24] [25]. This process is characterized by activation energies of approximately 28.5 kJ/mol under thermal conditions, with the reaction proceeding through a transition state where the attacking nucleophile forms a bond with one sulfur atom while the sulfur-sulfur bond is simultaneously broken [24] [25]. The mechanism is first order in both disulfide substrate and hydroxide concentration, confirming the bimolecular nature of the process [24] [25].

Alternative disulfide bond breaking mechanisms involve direct carbon-sulfur bond rupture, which becomes competitive under mechanochemical conditions [24]. The activation energy for carbon-sulfur bond cleavage is significantly higher (45.2 kJ/mol) under thermal conditions compared to the SN2 mechanism, but this difference decreases dramatically under applied mechanical force [24]. At forces of approximately 2 nN, the activation energies for both mechanisms become nearly equivalent, leading to competition between the two pathways [24].

The sulfur-sulfur bond cleavage mechanism represents a third pathway for disulfide bond breaking, characterized by the highest activation energy (52.8 kJ/mol) under thermal conditions [24]. This mechanism involves direct homolytic cleavage of the sulfur-sulfur bond without the involvement of external nucleophiles [24]. The process is facilitated by applied mechanical force, with the activation energy decreasing to 14.2 kJ/mol at forces of 2 nN [24].

Alpha-elimination mechanisms provide an alternative route for disulfide bond breaking through the removal of α-protons by hydroxide ions [24]. This process involves the abstraction of hydrogen atoms adjacent to the sulfur centers, leading to the formation of carbanion intermediates that subsequently undergo elimination to break the disulfide bond [24]. The activation energy for this mechanism is 29.1 kJ/mol under thermal conditions, making it competitive with the SN2 pathway [24].

Beta-elimination mechanisms involve the removal of β-protons from positions further removed from the sulfur centers [24]. While this mechanism is less favorable than α-elimination due to the greater distance between the elimination site and the sulfur centers, it can still contribute to disulfide bond breaking under certain conditions [24]. The activation energy for β-elimination is approximately 38.7 kJ/mol, making it less competitive than other mechanisms [24].

Free radical mechanisms for disulfide bond breaking have been demonstrated through studies using covalently-attached radical species [23]. These mechanisms involve direct radical substitution at sulfur centers, with activation energies of approximately 22.3 kJ/mol under thermal conditions [23]. The process is characterized by the formation of sulfur-centered radicals that facilitate bond breaking through homolytic pathways [23].

The force-dependence of disulfide bond breaking mechanisms reveals significant mechanochemical effects [24] [25]. Applied tensile forces can dramatically alter the relative activation energies of different pathways, leading to changes in the dominant mechanism [24] [25]. For example, carbon-sulfur bond rupture becomes increasingly favorable under applied force, with the activation energy decreasing from 45.2 kJ/mol at zero force to 12.1 kJ/mol at 2 nN [24].

The coupling between mechanical force and reaction coordinates varies significantly among different disulfide bond breaking mechanisms [24] [25]. Mechanisms involving direct bond rupture show high force sensitivity, with activation energies decreasing rapidly as force increases [24] [25]. In contrast, mechanisms involving proton abstraction show lower force sensitivity, with activation energies remaining relatively constant even under applied force [24] [25].

Single-molecule force spectroscopy studies have provided experimental validation of theoretical predictions regarding disulfide bond breaking mechanisms [25]. These experiments demonstrate that the rate of disulfide bond reduction increases exponentially with applied force, with rate enhancements of up to 10-fold observed over a 300 pN force range [25]. The force-dependent kinetics are consistent with theoretical predictions of bond lengthening at the transition state [25].

The pH dependence of disulfide bond breaking mechanisms provides insights into the role of protonation states in determining reaction pathways [24] [25]. Under acidic conditions, the availability of hydroxide ions for nucleophilic attack is limited, favoring alternative mechanisms such as direct bond rupture [24]. Under alkaline conditions, the SN2 mechanism becomes dominant due to the high concentration of hydroxide nucleophiles [24].