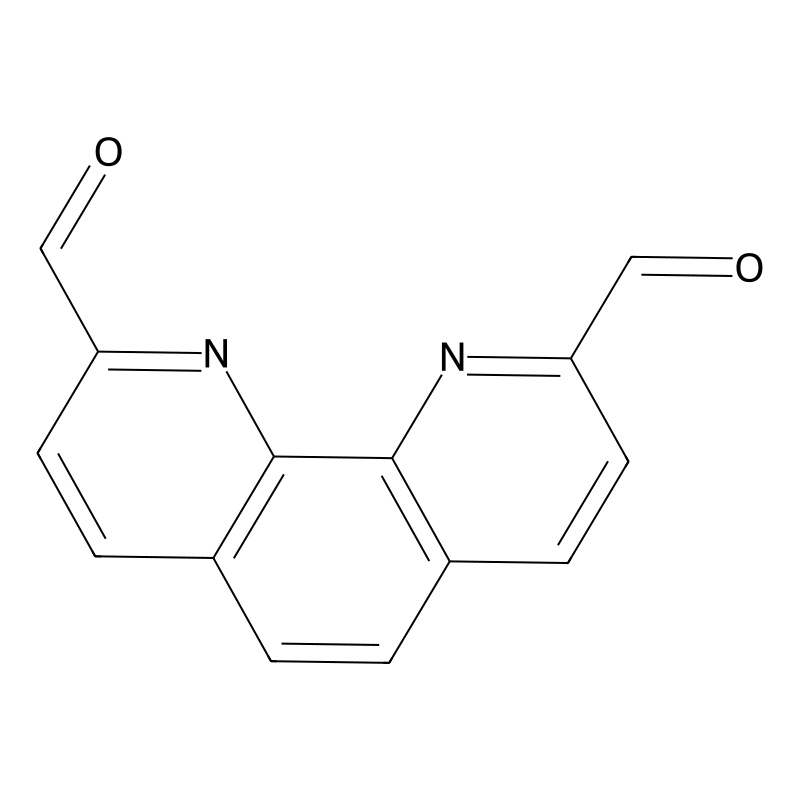
1,10-Phenanthroline-2,9-dicarbaldehyde

1,10-Phenanthroline-2,9-dicarbaldehyde is a bifunctional aromatic aldehyde built upon the 1,10-phenanthroline (phen) scaffold. The core structure is characterized by its high rigidity, planarity, and strong chelating capability for a wide range of metal ions. The aldehyde groups at the 2 and 9 positions are synthetically accessible handles, primarily for Schiff base condensation reactions, making this compound a key precursor for constructing multidentate ligands, complex supramolecular architectures, and luminescent materials. Its structural properties are not merely incidental but are central to its function as a pre-organized building block in advanced synthesis.

Substituting 1,10-phenanthroline-2,9-dicarbaldehyde with more common or flexible analogs, such as 2,2'-bipyridine-6,6'-dicarboxaldehyde, is a critical design change, not a simple material swap. The fixed, planar geometry of the phenanthroline core restricts conformational freedom, pre-organizing the aldehyde groups into a specific orientation. This intrinsic rigidity is essential for creating sterically defined metal complexes and for directing the high-fidelity self-assembly of complex architectures. In contrast, the rotational freedom of the C-C bond in bipyridine analogs introduces conformational uncertainty, which can inhibit the formation of desired products. For applications where the ligand framework dictates catalytic activity or selectivity, the phenanthroline scaffold has been shown to be essential, with bipyridine-based analogs proving completely inactive in certain systems. Therefore, selecting this compound is a deliberate choice for structural control that cannot be replicated by more flexible or electronically different precursors.

Catalytic Activity: Bipyridine Analogs Inactive

In the development of base-metal catalysts for alkene hydrosilylation, the choice of ligand scaffold is critical to performance. An iron catalyst featuring a 2,9-diaryl-1,10-phenanthroline ligand framework achieved a product yield of >99% for the hydrosilylation of 1,2-diphenylpropene. Under identical reaction conditions, a catalyst using an analogous 2,2'-bipyridine scaffold was reported to be 'totally inactive,' yielding 0% of the desired product.

This demonstrates that for specific catalytic systems, the rigid electronic and steric profile of the phenanthroline core is indispensable for activity, making it a non-interchangeable component.

Avoids Hazardous Selenium Dioxide Oxidation

The standard laboratory synthesis of 1,10-phenanthroline-2,9-dicarbaldehyde involves the oxidation of 2,9-dimethyl-1,10-phenanthroline (neocuproine) using selenium dioxide (SeO2). This established procedure requires refluxing for several hours with a toxic oxidizing agent, often yielding the product in the 62-70% range after purification.

Procuring this compound directly offers significant advantages in process efficiency and safety, saving hours of reaction time, avoiding the handling and disposal of toxic selenium compounds, and bypassing a moderate-yield purification step.

Pre-Organized Structure for Macrocyclization

The rigid, planar structure of the phenanthroline core serves as a geometric template, locking the 2,9-dicarbaldehyde groups into a fixed orientation. This pre-organization is a key advantage for template-directed synthesis of macrocycles and other complex architectures. Compared to the flexible 2,2'-bipyridine core, which allows free rotation around its central C-C bond, the phenanthroline scaffold reduces the entropic penalty of cyclization and minimizes the formation of undesired oligomeric or polymeric side products, leading to more predictable and higher-yield assemblies.

For syntheses where a specific, rigid final geometry is the primary goal, this compound provides a more reliable and predictable outcome than flexible alternatives, justifying its selection for high-fidelity synthetic routes.

Macrocyclic Ligands for Selective Metal Separation

This compound is the precursor of choice for synthesizing structurally defined macrocyclic ligands, such as diamides and Schiff bases. The rigidity of the phenanthroline backbone is critical for creating pre-organized cavities for selective complexation, a property exploited in ligands designed for the separation of f-elements like americium and europium in nuclear waste processing.

Scaffold for High-Performance Homogeneous Catalysts

Where ligand geometry is crucial for catalytic activity and selectivity, this building block provides a superior framework. It is the correct choice for developing catalysts where flexible bipyridine analogs are known to underperform or fail, as demonstrated in certain iron-catalyzed hydrosilylation reactions.

Key Component for Helicates and Programmed Supramolecular Systems

The defined stereochemical information encoded in the rigid phenanthroline backbone makes it an ideal component for the programmed self-assembly of complex, multi-component architectures such as double- and triple-stranded helicates. Its use ensures higher fidelity in the formation of these intricate structures compared to more flexible building blocks.