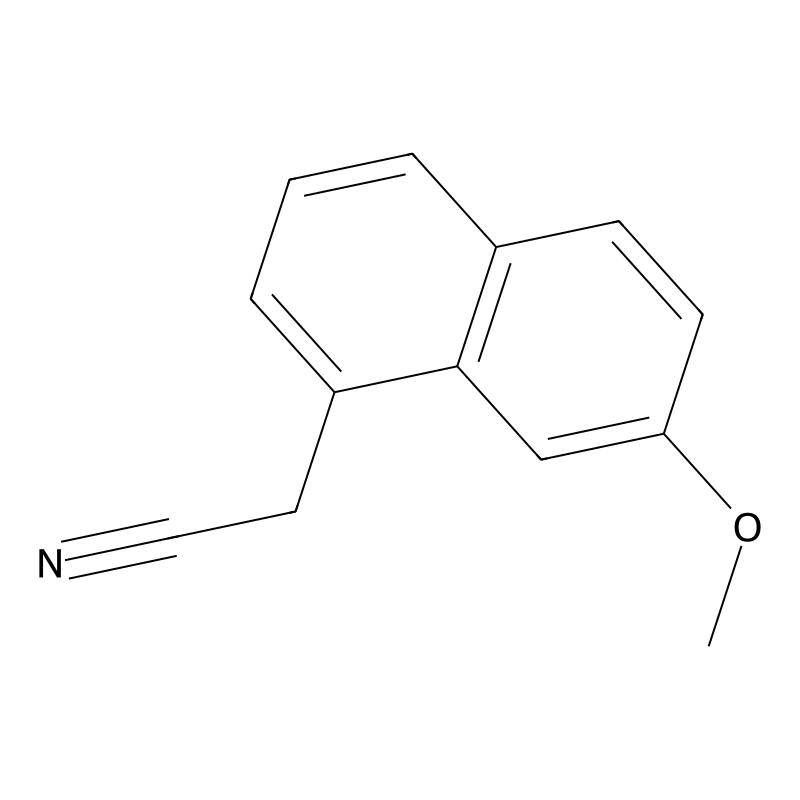
7-Methoxy-1-naphthylacetonitrile

7-Methoxy-1-naphthylacetonitrile (CAS 138113-08-3) is a highly stable, functionalized aromatic nitrile widely procured as the critical late-stage intermediate for the synthesis of the melatonergic antidepressant Agomelatine. Structurally characterized by a fused naphthalene core with a methoxy group at the 7-position and an acetonitrile side chain at the 1-position, this compound provides a pre-aromatized framework that is highly reactive toward catalytic hydrogenation. By procuring this specific intermediate, chemical manufacturers can bypass complex upstream ring-oxidation steps, enabling a streamlined, high-yield reduction and acetylation sequence directly to the final active pharmaceutical ingredient (API) [1].

Substituting 7-Methoxy-1-naphthylacetonitrile with upstream precursors like 7-methoxy-1-tetralone or 7-methoxy-3,4-dihydro-1-naphthylacetonitrile introduces severe process bottlenecks. The unaromatized dihydro-precursor requires harsh dehydroaromatization, which typically relies on either polluting oxidants like DDQ—generating stoichiometric DDHQ waste—or expensive, easily poisoned palladium/ruthenium catalysts under reflux conditions [1]. Alternatively, using the structurally related (7-methoxy-1-naphthyl)acetic acid necessitates a longer sequence of esterification and amidation steps [2]. Procuring the exact pre-aromatized nitrile ensures a streamlined, one- or two-step reductive acetylation process, avoiding toxic byproducts and ensuring the high purity required for pharmaceutical applications.

Elimination of Dehydroaromatization Bottlenecks

Synthesizing the naphthalene core from upstream precursors like 7-methoxy-3,4-dihydro-1-naphthylacetonitrile requires a challenging dehydroaromatization step. Traditional methods using DDQ achieve only moderate yields (approximately 76%) while generating stoichiometric DDHQ waste, and catalytic methods require expensive Pd/C under reflux. Procuring 7-Methoxy-1-naphthylacetonitrile bypasses this step entirely, eliminating catalyst poisoning risks and environmental constraints[1].

Bypassing the aromatization step reduces catalyst costs, eliminates toxic byproducts, and simplifies the purification of the final API.

Superior Overall Yield in API Production

When starting from the upstream precursor 7-methoxy-1-tetralone, the traditional 8-step synthesis of Agomelatine yields less than 30% overall. In contrast, utilizing 7-Methoxy-1-naphthylacetonitrile as the starting material allows for a direct catalytic hydrogenation (e.g., using Raney Nickel or NiO nanoparticles) and acetylation, achieving total yields exceeding 81.8% with HPLC purities of 99.2%[1].

A massive increase in overall yield directly translates to lower cost of goods sold (COGS) and higher throughput for commercial API manufacturing.

Streamlined Amidation vs. Carboxylic Acid Analogs

Alternative synthesis routes utilize (7-methoxy-1-naphthyl)acetic acid as an intermediate, which requires esterification, amidation, and subsequent reduction steps to form the target ethylamine framework. 7-Methoxy-1-naphthylacetonitrile, possessing a reactive nitrile group, enables direct reductive acetylation to the target N-acetylamine, cutting out multiple intermediate isolation steps [1].

Reducing the number of synthetic steps minimizes solvent usage, decreases cycle times, and lowers the risk of intermediate degradation.

Commercial Synthesis of Agomelatine

The primary industrial application is the direct catalytic hydrogenation and acetylation of this compound to produce the melatonergic antidepressant API, Agomelatine. Procuring the pre-aromatized nitrile is critical for bypassing low-yield upstream oxidation steps and achieving >80% overall yields [1].

Development of Novel Melatonin Receptor Agonists

R&D teams utilize this compound as a rigid, functionalized naphthalene building block to design next-generation MT1/MT2 agonists or 5-HT2C antagonists, leveraging the reactive nitrile for diverse amine and amide derivations[2].

Advanced Catalysis Benchmarking

In chemical engineering, this compound serves as a standard substrate to evaluate the efficiency of novel hydrogenation catalysts (e.g., NiO nanoparticles, Raney Nickel variants) for the selective reduction of aromatic nitriles to primary amines in one-pot reactions [3].