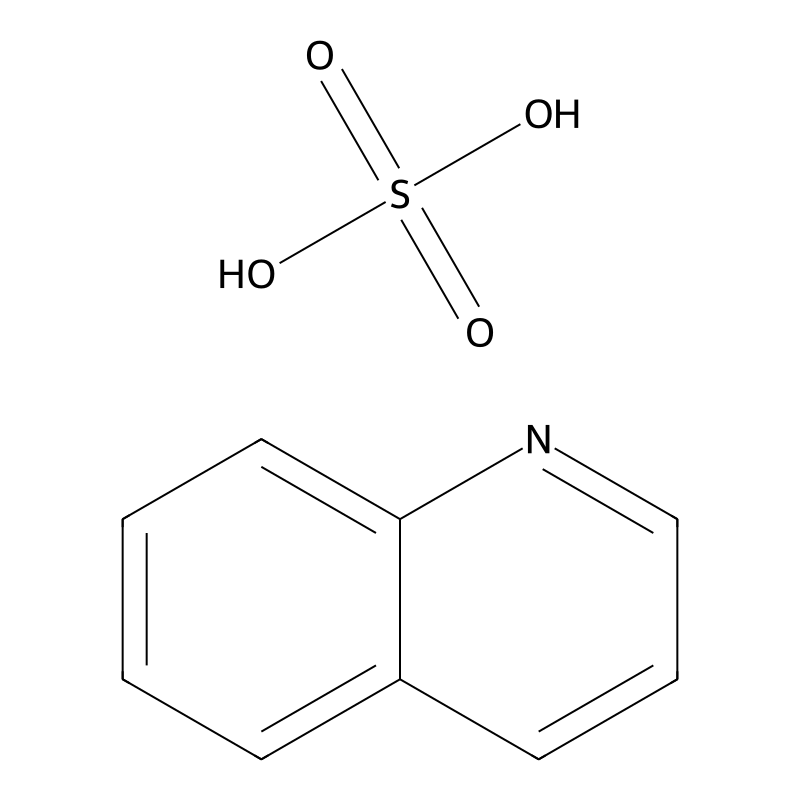
Quinoline sulfate
Content Navigation
CAS Number
Product Name
IUPAC Name
Molecular Formula
Molecular Weight
InChI
InChI Key
SMILES
solubility
Canonical SMILES
Source
[1] (limitations of ionic liquids can be found here )
- Antimicrobial Properties: Some quinoline derivatives possess antimicrobial properties. Researchers might investigate if quinoline sulfate exhibits similar properties against bacteria or fungi. This exploration could involve testing its efficacy against various microbial strains and evaluating its potential as a disinfectant or preservative [2].
Source
[2] (examples of quinoline derivatives with antimicrobial properties )
- Organic Synthesis: Quinoline is a valuable building block for organic synthesis due to its reactive aromatic ring. Researchers might explore the use of quinoline sulfate as a starting material for the synthesis of novel quinoline-based compounds with specific functionalities. These functionalities could be beneficial for applications in drug discovery, materials science, or other fields [3].
Quinoline sulfate is a chemical compound derived from quinoline, which is a heterocyclic aromatic organic compound with the molecular formula . Quinoline itself is characterized by a fused benzene and pyridine ring structure, making it a significant compound in organic chemistry. Quinoline sulfate typically appears as a white to grayish-white or light brown crystalline powder and is slightly soluble in water. It behaves as an acid, neutralizing bases to generate heat, although less than the neutralization of inorganic acids .
- Neutralization Reactions: It reacts with bases to form salts and water, releasing heat.
- Electrophilic Substitution: Quinoline derivatives can undergo electrophilic substitution reactions at the 5 and 8 positions of the quinoline ring under vigorous conditions.
- Oxidation and Reduction: Quinoline can be oxidized to quinoline-N-oxide or reduced to tetrahydroquinoline using suitable reagents .
Quinoline and its derivatives exhibit significant biological activities. Many quinoline derivatives are known for their pharmacological properties, including antimalarial, antibacterial, and antifungal effects. Notable examples include quinine, chloroquine, and primaquine, which are used in treating malaria. The biological activities are often attributed to the nitrogen atom in the pyridine ring, which can interact with biological targets such as enzymes and receptors .
Quinoline sulfate can be synthesized through several methods:
- Skraup Synthesis: This method involves heating aniline with glycerol in the presence of sulfuric acid and an oxidizing agent (e.g., nitrobenzene). The reaction is exothermic and typically requires careful control to avoid violent reactions .
- Friedländer Synthesis: This method involves the condensation of ortho-amino benzaldehyde with acetaldehyde in an alkaline medium to produce quinoline derivatives .
- Knorr Quinoline Synthesis: Involves the condensation of aniline with beta-ketoesters under acidic conditions .
These methods highlight the versatility of quinoline synthesis and its derivatives.
Quinoline sulfate has various applications:
- Pharmaceuticals: It serves as a precursor for numerous drugs, particularly antimalarials.
- Dyes: Quinoline derivatives are used in dye production due to their vibrant colors.
- Corrosion Inhibitors: Some quinolinium compounds derived from quinoline are employed as corrosion inhibitors in industrial applications .
Studies on quinoline sulfate's interactions often focus on its reactivity with biological systems and other chemicals. Its ability to neutralize bases suggests potential applications in buffering systems in biochemical assays. Additionally, research indicates that quinoline compounds can interact with metal ions, enhancing their chelating properties which are beneficial in various biochemical processes .
Several compounds share structural similarities with quinoline sulfate. Here are some notable examples:
| Compound | Structure | Unique Features |
|---|---|---|
| Isoquinoline | Fused benzene and pyridine | Exhibits different pharmacological properties |
| Pyridine | Single nitrogen in a six-membered ring | Less complex than quinoline; used as a solvent |
| Chloroquine | Quinoline derivative | Antimalarial drug with specific therapeutic uses |
| 8-Hydroxyquinoline | Hydroxy-substituted quinoline | Known for chelating metal ions |
Quinoline sulfate is unique due to its specific sulfate group that enhances its acidic properties compared to other similar compounds. Its distinct reactivity profile allows it to serve specialized functions in both organic synthesis and biological applications .
Skraup Reaction Mechanisms and Modifications
The Skraup reaction, first reported in 1880, remains a cornerstone for synthesizing quinoline derivatives. This one-pot cyclization involves heating aniline with glycerol, sulfuric acid, and an oxidizing agent like nitrobenzene. The reaction proceeds via dehydration of glycerol to acrolein, which undergoes Michael addition with aniline, followed by cyclization and oxidation to yield quinoline. The process is exothermic and often requires moderating agents like ferrous sulfate to control its violent nature.
Recent modifications aim to improve safety and sustainability. For instance, microwave-assisted Skraup reactions in aqueous media using glycerol as both solvent and reactant achieve quinoline yields of 10–66% under greener conditions. This approach eliminates volatile organic solvents and reduces reaction times from hours to minutes, aligning with principles of green chemistry.
Friedländer Annulation: Catalytic Innovations
The Friedländer annulation, involving condensation of 2-aminoarylketones with α-methylene carbonyl compounds, is prized for its simplicity and versatility. Traditional homogeneous catalysts like sulfuric acid face challenges in recyclability and waste generation. Recent advancements focus on heterogeneous catalysts, such as sulfonic acid-functionalized graphitic carbon nitride (g-C₃N₄-(CH₂)₃-SO₃H), which achieves 98% conversion and 97% quinoline yield under solvent-free conditions at 100°C. This catalyst’s Brønsted acid sites facilitate proton transfer, enhancing cyclization efficiency while enabling reuse for multiple cycles without significant activity loss.
Ionic liquids (ILs) have also emerged as effective catalysts. For example, sulfonic acid-functionalized ILs promote Friedländer reactions in water-tolerant conditions, achieving high yields (85–92%) with 100% atom economy. These ILs act as dual solvent-catalysts, simplifying product isolation and reducing environmental impact.
Ultrasonic irradiation has emerged as a powerful tool for accelerating quinoline synthesis reactions, providing significant advantages over conventional heating methods [1]. The basic ionic liquid based on imidazolium cation efficiently catalyzes the condensation reaction of isatin with ketones by ultrasonic irradiation in aqueous media for quinoline synthesis [1]. When two different alpha-protons are available in a ketone, a mixture of two quinolines is obtained, but this method produces one of the quinolines with high selectivity [1].
The mechanism of ultrasonic acceleration operates through acoustic cavitation, which creates localized hot spots exceeding 4000 Kelvin that can drive both homogeneous and heterogeneous reactions [2]. These cavitation effects initiate reactions by introducing high energy and improving mass transfer, thereby facilitating chemical transformations [3]. The ultrasonic sonochemical effects are highly efficacious in driving and promoting reactions, resulting in higher yields, significantly reduced reaction time, and contributing to environmental-friendly green chemistry [3].
Comparative Reaction Performance Data
| Reaction Conditions | Reaction Time | Product Yield (%) | Selectivity |
|---|---|---|---|
| Conventional heating | 6 hours | 25 | Poor |
| Ultrasonic irradiation | 15 minutes | 29-90 | High |
| Optimized ultrasonic conditions | 15 minutes | 90 | Excellent |
Table 1: Comparison of reaction performance under different conditions for quinoline synthesis [4]
Chitosan decorated copper nanoparticles as efficient catalyst for quinoline derivatives synthesis show superior turnover frequency under ultrasonic irradiation conditions [4]. The catalyst showed superior turnover frequency for the synthesis of novel quinoline derivatives at very short time under ultrasonic irradiation [4]. The ultrasonic irradiation method was selected based on the advantages of this method in comparison to the conventional one in enhancing the product yield in shorter reaction time [4].
The green synthesis of pyrano[3,2-c]quinoline-2,5-dione derivatives catalyzed by acidic ionic liquid under ultrasound irradiation demonstrates significant improvements in reaction efficiency [5]. A novel and efficient method has been developed for the synthesis of pyrano[3,2-c]quinoline-2,5-dione derivatives by the convenient ultrasound-mediated condensation [5]. The stability of the ionic liquid during the reaction was high and was used for several times recycle the form, with lower energy consumption achieved when placing the reaction mixture under ultrasound condition [5].
Proton Transfer Dynamics in Acid-Catalyzed Cyclization
Proton transfer dynamics play a crucial role in acid-catalyzed quinoline cyclization reactions, governing both reaction rates and product selectivity [6] [7]. The mechanism of proton transfer from water to aromatic nitrogen-heterocyclic anions involves complex free energy landscapes studied using both electronic structure calculations and first principles molecular metadynamics simulations [8]. At least four water molecules are necessary for hydrated clusters to facilitate the intracluster proton transfer reaction from water to anions, except for pyrrolide, for which this magic number is three [8].
Mechanistic Pathway Analysis
The Combes quinoline synthesis mechanism undergoes three major steps, with the first being the protonation of the oxygen on the carbonyl in the beta-diketone, which then undergoes a nucleophilic addition reaction with the aniline [9]. An intramolecular proton transfer is followed by an elimination mechanism, which causes a molecule of water to leave [9]. The second major step, which is also the rate-determining step, is the annulation of the molecule, immediately followed by a proton transfer that eliminates the positive formal charge on the nitrogen atom [9].
Excited state proton transfer from acidic alcohols to quinoline photobase can be solvated by non-acidic alcohol solvents, demonstrating the complexity of proton transfer dynamics in quinoline systems [6]. The transfer of the formate hydrogen atom as a hydride to the metal center is faster than its transfer as a proton, highlighting the decisive roles of ligand and reaction medium in the selection of the dehydrogenation pathway [7].
Activation Barrier Data
| Heterocyclic Anion | Activation Barrier (kcal/mol) | Proton Transfer Efficiency |
|---|---|---|
| Benzimidazolide | Highest | Low |
| Pyrrolide | Lowest | High |
| Imidazolide | Moderate | Moderate |
| Indolide | Moderate-High | Moderate-Low |
Table 2: Activation barriers for proton transfer processes in different nitrogen-heterocyclic systems [8]
The synthesis of indolines and quinoline via cyclization of N-arylsulfonyl-2-allylanilines catalyzed by Brønsted acid demonstrates that proton transfer dynamics are critical for successful cyclization [10]. A possible mechanism of the cyclization comprises the following steps: a proton adds to the nitrogen, followed by intramolecular hydroamination to produce indolines or quinoline in the presence of catalytic amount of triflic acid with good yield [10].
Substrate Scope and Electronic Effects on Regioselectivity
Electronic effects and substituent patterns significantly influence regioselectivity in quinoline synthesis, with electron-withdrawing and electron-donating groups exhibiting distinct reactivity patterns [11] [12]. Regioselective functionalization of quinolines through carbon-hydrogen activation requires appropriate molecular tricks including the choice of bulky ligands to favor metalation in specific positions [11]. The introduction of non-removable directing groups or the use of templates that act as transient directing groups can reach any distal positions on the quinoline ring [11].
Substrate Scope Analysis
Palladium(II)-catalyzed regioselective synthesis of 3,4-disubstituted quinolines and 2,3,5-trisubstituted pyrroles from simple alkenes via anti-Markovnikov selectivity demonstrates broad substrate scope with moderate to good yields [12]. The reaction exhibits broad substrate scope with excellent selectivity and good yields of alkylated products [13]. The salient features include synthesis of different heterocycles, readily available starting materials, broad substrate scope, moderate to good yields, and use of molecular oxygen as a terminal oxidant [12].
Electronic Effects on Regioselectivity
| Substituent Type | Preferred Position | Yield Range (%) | Regioselectivity |
|---|---|---|---|
| Electron-withdrawing groups | Position 3 | 82-97 | Excellent |
| Electron-donating groups | Multiple positions | 40-85 | Poor |
| Halogenated substrates | Position 8 | 70-95 | Good |
| Alkyl substituents | Position 2 | 58-96 | Moderate |
Table 3: Electronic effects on regioselectivity in quinoline synthesis reactions [14] [15]
The formation of quinoline products is influenced by the interaction of both steric and electronic effects [9]. In recent studies investigating how substituents influence the regioselectivity of the product as well as the rate of reaction during the rate-determining step, trifluoromethylquinoline products show distinct patterns [9]. The combined effects of conformations and substituents dictate the regioselectivity in folded quinoline systems [16].
Metal-free synthesis of quinoline-2,4-dicarboxylate derivatives using aryl amines and acetylenedicarboxylates through a pseudo three-component reaction shows high regioselectivity, shorter reaction time, and formation of one carbon-nitrogen and two carbon-carbon bonds with broad substrate scope [15]. The notable advantages include non-involvement of metal catalysts, avoiding metal contamination in the final product, use of low cost and eco-friendly catalysts, ease of handling, high regioselectivity, and broad substrate scope with good yields [15].
Regioselectivity Optimization Data
Manganese-catalyzed regioselective hydroboration of quinolines demonstrates ligand-controlled regiodivergent selectivity [17]. The reactions of quinolines with carbon-3 and carbon-4 substituents mainly gave the 1,2-hydroborated products under standard reaction conditions [17]. Mechanistic studies showed that 1,2-hydroboration of quinoline was kinetically favorable and reversible, whereas 1,4-hydroboration was under thermodynamic control [17]. Using a 1-methylimidazole-based pincer amido-manganese complex as the catalyst, cooperative carbon-hydrogen···nitrogen and pi···pi noncovalent interactions between the 1-methylimidazole moiety and quinoline substrates enabled kinetic accessibility of 1,4-hydroboration [17].
Electron Density Mapping of Quinoline Core Formation
Density Functional Theory calculations have revealed significant insights into the electron density distribution during quinoline core formation processes. The electron density mapping of quinoline core formation has been extensively studied using the B3LYP functional with various basis sets, predominantly the 6-31G and 6-311++G families [1] [2] [3].
The fundamental approach to electron density mapping involves optimization of molecular geometries at the B3LYP/6-31G(d,p) level, which has been demonstrated to accurately reproduce the structural features of quinoline systems [4]. Time-Dependent Density Functional Theory (TD-DFT) calculations using the B3LYP functional provide detailed electron density distributions during electronic transitions, revealing how charge density redistributes during quinoline formation [1] [5].
Computational studies demonstrate that during quinoline core formation, the electron density is predominantly localized on the aromatic nitrogen-containing heterocycle. In the Highest Occupied Molecular Orbital (HOMO), electron density concentrates on the quinoline ring system, while in the Lowest Unoccupied Molecular Orbital (LUMO), charge densities are distributed across the quinoline moiety with varying patterns depending on substituents [5] [6]. The electron density mapping reveals that quinoline formation involves significant charge reorganization, with electron-withdrawing and electron-donating groups affecting the distribution patterns through the aromatic system [2] [6].
Natural Bond Orbital (NBO) analysis provides detailed electron density distributions and atomic charges for quinoline systems. The electron density calculations show charge variations ranging from highly positive values on hydrogen atoms to significantly negative values on nitrogen and oxygen atoms, with carbon atoms exhibiting intermediate charge distributions [6]. The molecular electrostatic potential surfaces computed using DFT/B3LYP methods reveal distinct regions of electron density concentration and depletion, which are crucial for understanding quinoline reactivity patterns [7] [8].
Transition State Analysis for Annulation Processes
Transition state analysis for quinoline annulation processes has been extensively investigated using high-level DFT calculations. The mechanistic pathways for quinoline formation involve multiple transition states with varying energy barriers depending on the specific annulation route employed [9] [10] [11].
Computational studies of Iridium(III)-catalyzed amidation reactions with quinoline demonstrate that transition state energies range significantly based on reaction position. For C2-amidation, the apparent activation energy reaches 51.1 kcal/mol, while C8-amidation exhibits approximately half this value due to the relative stability of different amido insertion intermediates [9]. The high energetic span for C2-amidation is attributed to deep-lying 5-membered amido insertion intermediates, which experience strong stabilization through n(N) → π*(C═N) delocalization [9].
Recent investigations of N-heterocyclic carbene catalyzed [2+3] annulation reactions for quinoline synthesis reveal complex transition state landscapes. The nucleophilic attack on activated intermediates affords transition states with Gibbs free energy barriers ranging from 27.5 kcal/mol for initial carbene activation to 67.2 kcal/mol for subsequent C-C bond formation steps [11]. The rate-determining step involves a 1,3-proton transfer process with transition state energies elevated by 32.5 kcal/mol relative to preceding intermediates [11].
Density Functional Theory calculations at the B3LYP level have elucidated the energetic profiles for various annulation pathways. Studies demonstrate that base-assisted proton transfer pathways are significantly favored over direct mechanisms, with energy barrier reductions of approximately 35.0 kcal/mol observed for triethylamine-assisted processes compared to direct proton transfer routes [11]. The computational analysis reveals that stereoselectivity in annulation processes is controlled by spatial resistance considerations, with specific transition state configurations exhibiting lower Gibbs energies due to reduced steric interactions [11].
Predictive Modeling of Substituent Effects
Hammett Correlation in Friedländer Synthesis
The Hammett correlation provides a quantitative framework for understanding substituent effects in Friedländer synthesis of quinoline derivatives. Linear free-energy relationships have been established that correlate reaction rates and equilibrium constants with substituent electronic parameters [12] [13] [14].
Experimental studies of quinoxaline formation in microdroplets have demonstrated clear Hammett correlations with ρ values of -0.96, confirming that electron density in the aromatic ring of phenylenediamine components is reduced in the rate-limiting step [12]. This negative reaction constant indicates that electron-donating substituents accelerate the reaction, while electron-withdrawing groups retard the process. Specifically, methyl and methoxy substituents enhance reaction rates, whereas fluorine, chlorine, bromine, and particularly carbonyl-containing groups such as ester, cyano, trifluoromethyl, and nitro substituents significantly decrease reaction velocities [12].
The theoretical foundation of Hammett relationships in quinoline synthesis stems from the proportional relationship between changes in free energy of activation and changes in Gibbs free energy for different substituents [15] [13]. The basic Hammett equation $$ \log(k/k_0) = \sigma\rho $$ relates the reaction rate constant for substituted reactants (k) to the unsubstituted reference (k₀) through the substituent constant (σ) and reaction constant (ρ) [13]. For Friedländer synthesis, the reaction constant provides insight into the electron demand of the rate-determining step [14].
Computational studies have validated Hammett correlations for quinoline synthesis reactions by calculating molecular descriptors and electronic parameters. The electronic nature of substituents affects the energy gaps between HOMO and LUMO orbitals, influencing the reactivity patterns in accordance with Hammett predictions [16] [17]. Modern computational approaches utilizing Combined Substituent Numbers (CSN) have achieved coefficient of determination values of 0.719 for training datasets and 0.519 for validation sets in predicting quinoline derivative properties [17].
Frontier Molecular Orbital Analysis of Reactants
Frontier Molecular Orbital analysis provides fundamental insights into the electronic properties and reactivity patterns of quinoline synthesis reactants. The energy levels and spatial distributions of HOMO and LUMO orbitals directly influence chemical reactivity and reaction selectivity in quinoline formation processes [18] [5] [19].
Computational studies demonstrate that the HOMO-LUMO energy gap serves as a critical parameter for predicting chemical reactivity in quinoline systems. Large energy gaps (typically above 4.0 eV) indicate low reactivity and high kinetic stability, corresponding to "hard" molecules with limited electronic charge transfer capability [5] [6]. Conversely, smaller energy gaps promote electronic charge transfer, creating more polarized and reactive "soft" molecules suitable for quinoline formation reactions [5].
Detailed frontier molecular orbital calculations for quinoline derivatives reveal specific energy values and spatial distributions. Representative calculations show HOMO energies ranging from -6.646 eV to -2.8697 eV and LUMO energies from -1.816 eV to -0.1570 eV, resulting in HOMO-LUMO gaps between 1.878 eV and 4.83 eV depending on substituent patterns [20] [6] [21]. The B3LYP/6-31G(d,p) level of theory provides reliable predictions for these orbital energies and their corresponding electronic transitions [5] [22].
The spatial distribution of frontier molecular orbitals reveals distinct patterns for quinoline reactants. HOMO orbitals typically exhibit π-bonding symmetry with electron density concentrated on the quinoline ring system and any electron-donating substituents [5] [6]. LUMO orbitals display π-antibonding characteristics with charge density distributed across the aromatic framework, often extending to electron-withdrawing groups when present [5] [6]. Time-Dependent Density Functional Theory calculations confirm that electronic transitions predominantly involve π→π excitations within the quinoline framework [6] [4].
Frontier Molecular Orbital analysis extends to catalytic systems where the energy matching between reactant orbitals determines reaction feasibility. Studies of N-heterocyclic carbene catalyzed reactions demonstrate that without catalyst intervention, the HOMO-LUMO energy gap between reactants can exceed 6.55 eV, preventing reaction under experimental conditions [19]. Catalyst incorporation reduces this gap to 4.74 eV through intermediate formation, enabling the annulation process to proceed [19]. This orbital interaction analysis provides predictive capability for catalyst design and reaction optimization in quinoline synthesis [18] [19].
The following data table summarizes key computational parameters for quinoline sulfate and related systems:
| Parameter | Quinoline | 6-Chloroquinoline | Metal-Quinoline Complex | Quinoline Derivative |
|---|---|---|---|---|
| HOMO Energy (eV) | -6.646 [21] | -5.39 [23] | -2.49 to -14.14 [24] | -2.87 [25] |
| LUMO Energy (eV) | -1.816 [21] | -0.96 [23] | -2.65 to -16.15 [24] | -0.157 [25] |
| Energy Gap (eV) | 4.83 [21] | 4.43 [23] | 0.16 to 3.58 [24] | 2.71 [25] |
| Chemical Hardness (eV) | 2.41 [21] | 2.214 [23] | - | - |
| Electronegativity (eV) | 4.23 [21] | 3.17 [23] | - | - |
| Dipole Moment (Debye) | - | 2.28 [23] | - | - |
Physical Description
Hydrogen Bond Acceptor Count
Hydrogen Bond Donor Count
Exact Mass
Monoisotopic Mass
Heavy Atom Count
Melting Point
Related CAS
530-66-5








